2021算法这么清奇:如何从数学视角优化复杂度

复杂度
复杂度是程序时间损耗和数据总量之间的变化关系,通常用 O(f(n)) 来表示,其中 f(n) 就是复杂度函数。
如果程序的时间损耗和数据量的关系是 t=c+n×b,也就是说复杂度函数为 f(n)=c+n×b。
复杂度通常不关注常数,因为它是个固定的时间损耗,与输入的数据总量没有任何的关系。因此,复杂度函数 c+n×b 可以忽略常数 c 和 b,直接缩写为 f(n) = n,即第一个例子的复杂度为 O(n)。
如果程序的时间损耗和数据量没有关系,即 t=c,我们依然会忽略这个常数,直接用 O(1) 来表示。
复杂度的计算与程序的结构有着密切关系。通常而言,一个顺序结构或选择结构的代码的执行时间与数据量无关,复杂度就是 O(1);而对于循环结构而言,如果循环的次数与输入数据量的多少有关,就会产生复杂度了。
通常,一层循环的时间复杂度是 O(n);如果是两个循环的嵌套,时间复杂度是 O(n2);如果是三个循环的嵌套,则是 O(n^3)……
用数学来优化复杂度
设想一下,如果一段线上代码在输入变量很多的时候就会“卡死”,那么这一定是一款无法上线的系统。因此,时间复杂度的优化,是每个开发者必须具备的技能。
其实,时间复杂度的优化有很多办法。除了优化数据结构、优化代码结构、减少程序中不必要的计算等通用方法以外,还可以利用强大的数学知识来进行时间复杂度的优化。
我们来举几个例子。
在一个无序的数组中,只有一个数字
obj出现了一次,其他数字都出现了两次,尝试去查找出这个出现了一次的obj。
绝大多数程序员的代码逻辑,应该都是设计两层 for 循环:一层遍历每个数字,一层计算每个数字出现的次数,直到找到 obj。
代码如下:
a = [2,1,4,3,4,2,3]
for i in range(0,len(a)):
times = 0
for j in range(0,len(a)):
if a[i] == a[j]:
times += 1
if times == 1:
print a[i]
break
读代码:
第 2 行,开始 for 循环,并把计数的变量
times置为0;第 4 行,嵌套了一个 for 循环;
第 5 行开始,判断里外两层循环的值是否相等,如果相等,则
times加1;第 7 行,判断
times是否为1,如果为1说明a[i]在数组中只出现了一次,则打印并break跳出循环结束。
根据我们前面的结论,这段代码的复杂度是 O(n^2),而且单独借助数据结构等思想已经很难再进行程序的优化了。
然而,如果从数学视角来看,这段代码就可以进行如下优化:
a = [2,1,4,3,4,2,3]
result = a[0]
for i in range(1,len(a)):
result = result ^ a[i]
print result
在这里,利用了异或运算的性质:
满足交换律和结合律;
可以把相同元素计算为
0;0异或任何数字都是其本身。
这样,只要把数组 a 中所有元素都异或在一起,就得到了 obj。
此时,只需要一层 for 循环,复杂度是 O(n)。
我们再看下面一个例子。
输入一个正整数 n,求不大于 n 的所有偶数之和。例如输入 6,则输出 2、4、6 之和,为 12;输入5,则输出 2、4 之和,为 6。
这个题目的常规解法,是采用 for 循环,让 i 从 1 遍历到 n。如果 i 为奇数,则 continue;如果为偶数,则加到 result 变量中。
不难发现,复杂度是 O(n),代码如下:
import sys
n = int(sys.argv[1])
result = 0
for i in range(n+1):
if i % 2 == 0:
result += i
print result
我们再从数学的视角来看待这个问题,你就会发现这是个等差数列求和的问题,等差数列求和的公式为
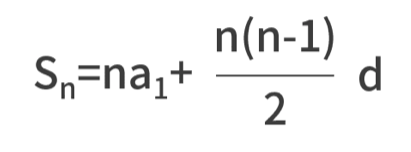
其中 a1 为首项,n 为项数,d 为公差,前 n 项和为 Sn。
利用这个公式,我们可以直接写出下面的代码:
import sys
n = int(sys.argv[1])
a1 = 0
d = 2
nn = n/2 + 1
print nn * a1 + 2 * nn * (nn - 1) / d
获得输入变量
n。求和的第一项,直接赋值为
0。公差
d为2。第 6 行,求项数。例如,输入 6,则项数为 6/3+1=4 项;输入 5,则项数为 5/2+1=3 项。
调用等差数列求和公式,直接得到结果,运行截图如下:

这段代码的执行与输入数据量 n 毫无关系,因此复杂度是 O(1)。
同样的道理,等比数列求和的代码,如果用计算机程序开发的思想,是需要一个 for 循环在 O(n) 复杂度下完成计算的。但借助等比数列求和公式,你只需要 O(1) 的复杂度就能得到结果。
小结
复杂度是程序开发中老生常谈的话题了。如果你的数学知识非常渊博,从数学的角度来降低代码复杂度也是一个不错的选择。
最后,可以练习一下:
输入一个正整数 n,求不大于 n 的所有 2 的正整数次幂的数字之和。例如,输入 17,则输出 1+2+4+8+16=31;输入 8,则输出 1+2+4+8=15。
你可以尝试两种方法来开发,分别是 O(n) 复杂度的 for 循环,和 O(1) 复杂度的等比数列求和公式。
推荐阅读:
更新不易,点个“在看”和“赞”吧(●'◡'●)!
