节点嵌入算法—Node2vec原理与优化
来源:https://zhuanlan.zhihu.com/p/267371107
本文从基础知识开始,一步一步引出Node2vec算法并给出了优化策略,保证阅读0门槛,如果觉得篇幅太长读不完建议先收藏起来哦~
背景知识-图结构
在介绍Node2vec之前,我们先从图开始。
图是由节点和边组成的结构,如下图所示。它在我们生活中是很常见的,比如社交网络,蛋白质分子之间的相互作用网络等。
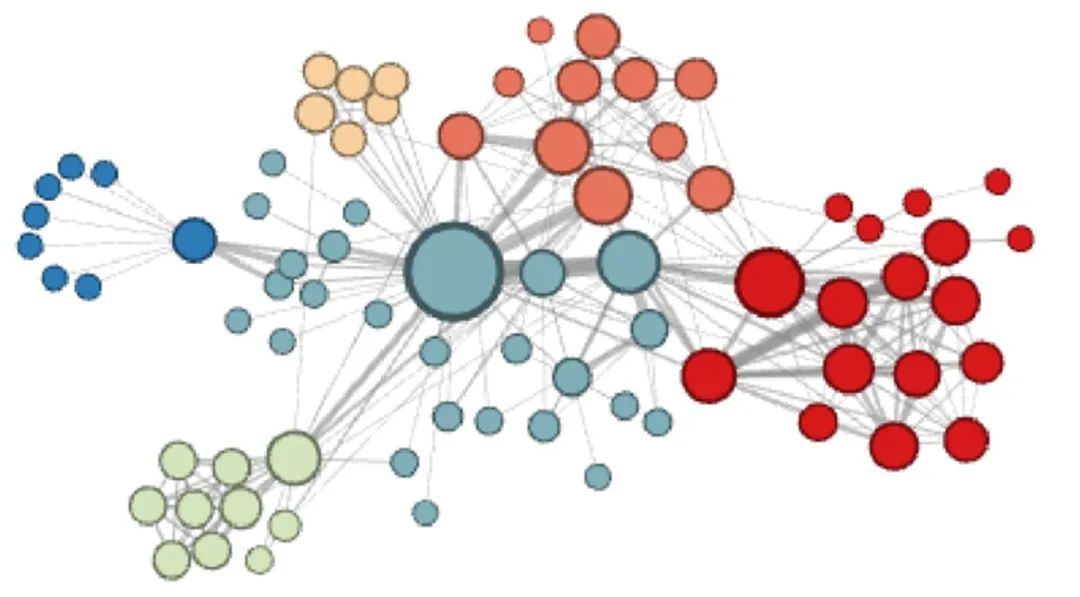
网络分析中的许多重要任务涉及对节点和边的预测,但是想要利用图中的信息是比较困难的,因为图本身是离散的。
因此,我们需要使用一种方式将图结构转化为便于计算的表达方式。
背景知识-嵌入算法
嵌入可以将实体映射到连续的向量空间中,使得实体可以用向量来表示。
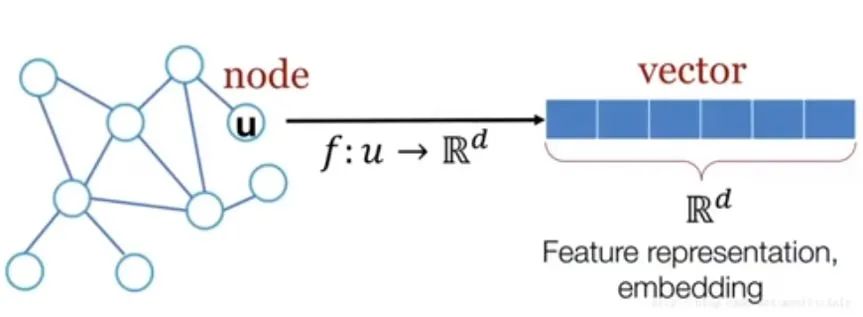
嵌入也有很多分类,这里Node2vec主要讨论点嵌入。
我们希望嵌入能够保留图中的信息,比如通过某个点的嵌入向量能够找到它在图中的邻居。同时,我们希望可以将某个点的嵌入向量直接用作下游任务的输入。
那么我们应该使用什么方法对某个点进行嵌入呢?
背景知识-SkipGram模型
在自然语言处理领域中也曾经遇到了类似的词嵌入问题,而其中一个有名的模型叫做SkipGram。
该模型使用一个滑窗对句子进行采样,使得中心词和滑窗内的单词同时出现的概率大,而中心词和滑窗外的单词同时出现的概率小, 来保证模型能够学习到某个单词的周围词信息。
采样的结果是一系列的由中心词和相邻词组成的单词对,正如图片中所展示的那样。

在对文本进行采样以后,Skipgram模型的第二步是将采样获取到的中心词转化为one-hot编码,并作为神经网络的输入,而神经网络的输出则是相邻词的向量。
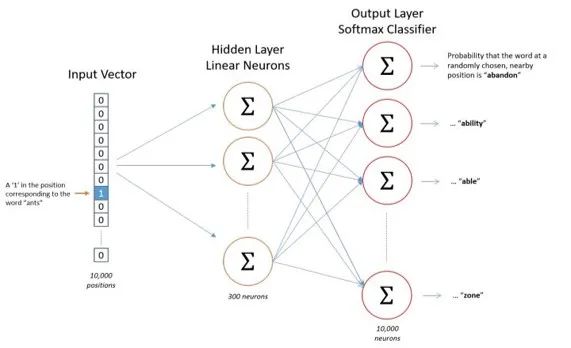
在经过一系列训练后,将某个中心词的one-hot向量与隐藏层的矩阵相乘获得的就是附近词的信息,即该词的词嵌入向量。
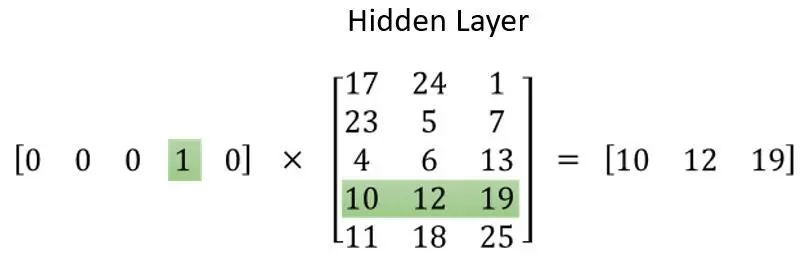
依照这个思路我们也可以将图中某个节点和它附近的节点嵌入到向量中,那么我们应该如何借鉴Skipgram模型对图中的节点进行嵌入呢?
背景知识-随机游走模型
Skipgram模型的输入是序列化的数据,这与图的结构化数据是不符合的,因此在应用Skipgram模型之前,我们需要获取节点的序列。
在此前的工作DeepWalk中提出了Random Walk的概念,具体来说就是从图中任意一个点出发,在节点之间等概率地转移,将上述步骤重复有限次,最终采集出一系列节点序列。
当收集到足够多的序列后,我们就可以用类似处理文本的方式,将这些序列输入Skipgram模型,并最终得到嵌入向量。

Node2vec算法-对随机游走模型提出质疑
简单的随机游走是存在问题的。
在Node2vec论文中指出,通过随机游走获取的节点序列不能同时反应图的同质性(homophily)和结构对等性(structural equivalence ),而这两种特性分别是由DFS和BFS体现的。
正如下图所示,蓝色箭头的采样序列反映了图的同质性而红色箭头的采样序列反映了图的结构对等性。

因此Node2vec提出采用一些参数来控制这个采样过程,使得这个采样过程既有DFS的特征也有BFS的特征。
Node2vec算法-对随机游走的改进
在Node2vec中,作者提出了采用一个搜索参数α来控制随机游走的倾向,该参数是由p、q两个值来确定的,定义如下:
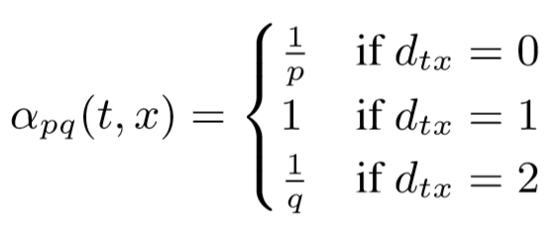
以下图为例,假设我们已经从t转移到v,接下来我们要采集新的节点。

如果p值比较小,那么采样将在t附近徘徊,表现出BFS的特征。
如果q值比较小,那么采样将逐渐远离t,表现出DFS的特征。
通过这种方式,我们可以对不同的图使用不同的采样策略,以此来得到质量更高的节点序列。这是Node2vec的一大贡献。
Node2vec算法-实验表现
作者在Link prediction和Node classification这两个任务上对Node2vec进行了实验。
结果表明,在这两项任务上Node2vec都取得了非常显著的进步。
在Node classification的部分数据集上,Node2vec甚至能达到20%的提升,这是非常惊人的,截取论文中的实验结果如下:
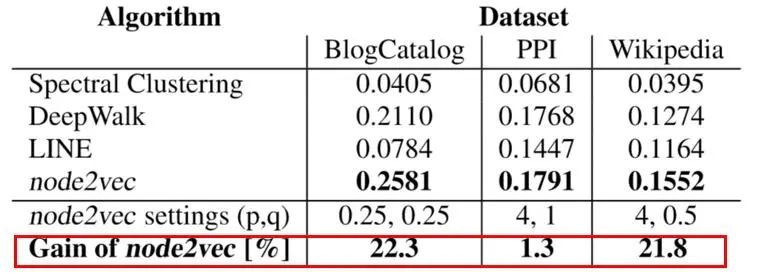
Node2vec优化-负采样加快计算速度
Node2vec依然有很多值得改进的地方。
我们再来看一眼这个Skipgram模型,隐藏层和输出层之间采用全连接的方式,这意味反向传播需要消耗大量计算资源。
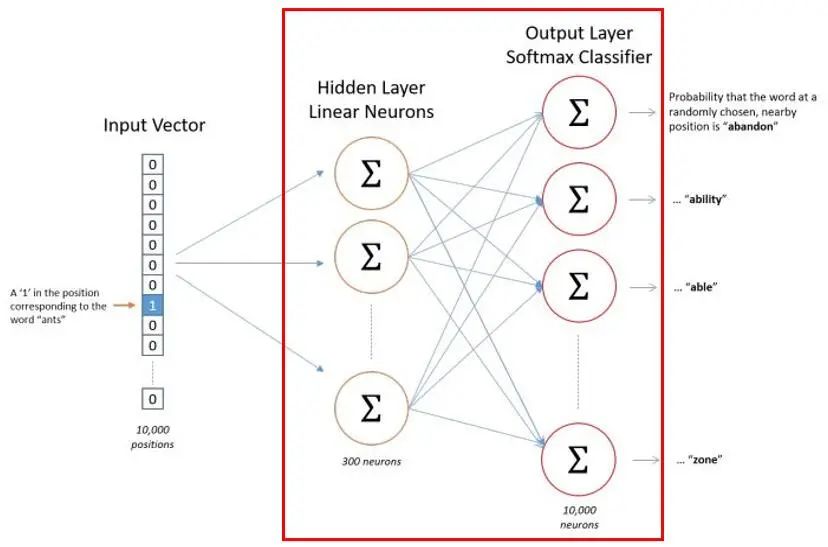
因此作者提出采用负采样的方式,在反向传播时更新隐藏层的部分权值,以此来减少计算量。
而权重是否被更新取决于权重相关的节点出现概率,节点出现概率越大,与之相关的权值被更新的概率也越大,权重被更新的概率可以表示如下:

(注意:公式中的0.75是一个经验结论,实际应用可以根据情况修改)
Node2vec优化-部分采样加快采样速度
对大规模的图采样极其消耗时间,因此我们可以对网络中的部分节点采样以节约采样耗时。
在部分采样中,我们需要控制节点被采样的概率,节点出现的频率Z(vi)越高,那么将它做为起点进行采样的概率就越小,可以理解为已经被反复采样的节点就不需要重新采样了,如下图所示:

(注意:公式中的0.001依然是一个经验结论,实际应用可以根据情况修改)
以上就是本文的所有内容啦~都看到这里了,不妨点个赞再走呗
··· END ···
↓长按关注本号、加我交流↓

