收藏！机器学习算法优缺点综述

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

   

    

     

      本文转自|视觉算法
     
    
   

目录

• 正则化算法（Regularization Algorithms）
• 集成算法（Ensemble Algorithms）
• 决策树算法（Decision Tree Algorithm）
• 回归（Regression）
• 人工神经网络（Artificial Neural Network）
• 深度学习（Deep Learning）
• 支持向量机（Support Vector Machine）
• 降维算法（Dimensionality Reduction Algorithms）
• 聚类算法（Clustering Algorithms）
• 基于实例的算法（Instance-based Algorithms）
• 贝叶斯算法（Bayesian Algorithms）
• 关联规则学习算法（Association Rule Learning Algorithms）
• 图模型（Graphical Models）

正则化算法（Regularization Algorithms）

它是另一种方法（通常是回归方法）的拓展，这种方法会基于模型复杂性对其进行惩罚，它喜欢相对简单能够更好的泛化的模型。

例子：

• 岭回归（Ridge Regression）
• 最小绝对收缩与选择算子（LASSO）
• GLASSO
• 弹性网络（Elastic Net）
• 最小角回归（Least-Angle Regression）

优点：

• 其惩罚会减少过拟合
• 总会有解决方法

缺点：

• 惩罚会造成欠拟合
• 很难校准

集成算法（Ensemble algorithms）

集成方法是由多个较弱的模型集成模型组，其中的模型可以单独进行训练，并且它们的预测能以某种方式结合起来去做出一个总体预测。

该算法主要的问题是要找出哪些较弱的模型可以结合起来，以及结合的方法。这是一个非常强大的技术集，因此广受欢迎。

• Boosting

• Bootstrapped Aggregation（Bagging）

• AdaBoost

• 层叠泛化（Stacked Generalization）（blending）

• 梯度推进机（Gradient Boosting Machines，GBM）

• 梯度提升回归树（Gradient Boosted Regression Trees，GBRT）

• 随机森林（Random Forest）

优点：

• 当先最先进的预测几乎都使用了算法集成。它比使用单个模型预测出来的结果要精确的多

缺点：

• 需要大量的维护工作

决策树算法（Decision Tree Algorithm）

决策树学习使用一个决策树作为一个预测模型，它将对一个 item（表征在分支上）观察所得映射成关于该 item 的目标值的结论（表征在叶子中）。

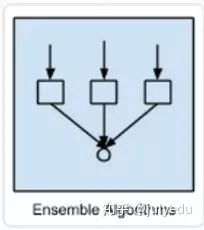
树模型中的目标是可变的，可以采一组有限值，被称为分类树；在这些树结构中，叶子表示类标签，分支表示表征这些类标签的连接的特征。

例子：

• 分类和回归树（Classification and Regression Tree，CART）
• Iterative Dichotomiser 3（ID3）
• C4.5 和 C5.0（一种强大方法的两个不同版本）

优点：

• 容易解释
• 非参数型

缺点：

• 趋向过拟合
• 可能或陷于局部最小值中
• 没有在线学习

回归（Regression）算法

回归是用于估计两种变量之间关系的统计过程。当用于分析因变量和一个 多个自变量之间的关系时，该算法能提供很多建模和分析多个变量的技巧。具体一点说，回归分析可以帮助我们理解当任意一个自变量变化，另一个自变量不变时，因变量变化的典型值。最常见的是，回归分析能在给定自变量的条件下估计出因变量的条件期望。

回归算法是统计学中的主要算法，它已被纳入统计机器学习。

例子：

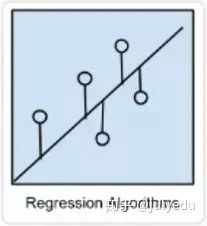
• 普通最小二乘回归（Ordinary Least Squares Regression，OLSR）
• 线性回归（Linear Regression）
• 逻辑回归（Logistic Regression）
• 逐步回归（Stepwise Regression）
• 多元自适应回归样条（Multivariate Adaptive Regression Splines，MARS）
• 本地散点平滑估计（Locally Estimated Scatterplot Smoothing，LOESS）

优点：

• 直接、快速
• 知名度高

缺点：

• 要求严格的假设
• 需要处理异常值

人工神经网络

人工神经网络是受生物神经网络启发而构建的算法模型。

它是一种模式匹配，常被用于回归和分类问题，但拥有庞大的子域，由数百种算法和各类问题的变体组成。

例子：

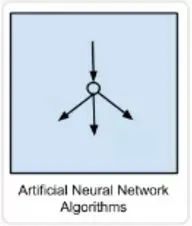
• 感知器
• 反向传播
• Hopfield 网络
• 径向基函数网络（Radial Basis Function Network，RBFN）

优点：

• 在语音、语义、视觉、各类游戏（如围棋）的任务中表现极好。
• 算法可以快速调整，适应新的问题。

缺点：

• 需要大量数据进行训练
• 训练要求很高的硬件配置
• 模型处于黑箱状态，难以理解内部机制
• 元参数（Metaparameter）与网络拓扑选择困难。

深度学习（Deep Learning）

深度学习是人工神经网络的最新分支，它受益于当代硬件的快速发展。

众多研究者目前的方向主要集中于构建更大、更复杂的神经网络，目前有许多方法正在聚焦半监督学习问题，其中用于训练的大数据集只包含很少的标记。

例子：

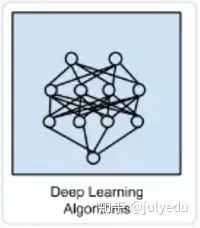
• 深玻耳兹曼机（Deep Boltzmann Machine，DBM）
• Deep Belief Networks（DBN）
• 卷积神经网络（CNN）
• Stacked Auto-Encoders

优点/缺点：见神经网络

支持向量机（Support Vector Machines）

给定一组训练事例，其中每个事例都属于两个类别中的一个，支持向量机（SVM）训练算法可以在被输入新的事例后将其分类到两个类别中的一个，使自身成为非概率二进制线性分类器。

SVM 模型将训练事例表示为空间中的点，它们被映射到一幅图中，由一条明确的、尽可能宽的间隔分开以区分两个类别。

随后，新的示例会被映射到同一空间中，并基于它们落在间隔的哪一侧来预测它属于的类别。

优点：

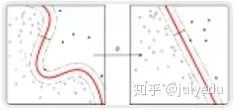
• 在非线性可分问题上表现优秀

缺点：

• 非常难以训练
• 很难解释

降维算法（Dimensionality Reduction Algorithms）

和集簇方法类似，降维追求并利用数据的内在结构，目的在于使用较少的信息总结或描述数据。

这一算法可用于可视化高维数据或简化接下来可用于监督学习中的数据。许多这样的方法可针对分类和回归的使用进行调整。

例子：

• 主成分分析（Principal Component Analysis (PCA)）
• 主成分回归（Principal Component Regression (PCR)）
• 偏最小二乘回归（Partial Least Squares Regression (PLSR)）
• Sammon 映射（Sammon Mapping）
• 多维尺度变换（Multidimensional Scaling (MDS)）
• 投影寻踪（Projection Pursuit）
• 线性判别分析（Linear Discriminant Analysis (LDA)）
• 混合判别分析（Mixture Discriminant Analysis (MDA)）
• 二次判别分析（Quadratic Discriminant Analysis (QDA)）
• 灵活判别分析（Flexible Discriminant Analysis (FDA)）

优点：

• 可处理大规模数据集
• 无需在数据上进行假设

缺点：

• 难以搞定非线性数据
• 难以理解结果的意义

聚类算法（Clustering Algorithms）

聚类算法是指对一组目标进行分类，属于同一组（亦即一个类，cluster）的目标被划分在一组中，与其他组目标相比，同一组目标更加彼此相似（在某种意义上）。

例子：

• K-均值（k-Means）
• k-Medians 算法
• Expectation Maximi 封层 ation (EM)
• 最大期望算法（EM）
• 分层集群（Hierarchical Clstering）

优点：

• 让数据变得有意义

缺点：

• 结果难以解读，针对不寻常的数据组，结果可能无用。

基于实例的算法（Instance-based Algorithms）

基于实例的算法（有时也称为基于记忆的学习）是这样学 习算法，不是明确归纳，而是将新的问题例子与训练过程中见过的例子进行对比，这些见过的例子就在存储器中。

之所以叫基于实例的算法是因为它直接从训练实例中建构出假设。这意味这，假设的复杂度能随着数据的增长而变化：最糟的情况是，假设是一个训练项目列表，分类一个单独新实例计算复杂度为 O（n）

例子：

• K 最近邻（k-Nearest Neighbor (kNN)）
• 学习向量量化（Learning Vector Quantization (LVQ)）
• 自组织映射（Self-Organizing Map (SOM)）
• 局部加权学习（Locally Weighted Learning (LWL)）

优点：

• 算法简单、结果易于解读

缺点：

• 内存使用非常高
• 计算成本高
• 不可能用于高维特征空间

贝叶斯算法（Bayesian Algorithms）

贝叶斯方法是指明确应用了贝叶斯定理来解决如分类和回归等问题的方法。

例子：

• 朴素贝叶斯（Naive Bayes）
• 高斯朴素贝叶斯（Gaussian Naive Bayes）
• 多项式朴素贝叶斯（Multinomial Naive Bayes）
• 平均一致依赖估计器（Averaged One-Dependence Estimators (AODE)）
• 贝叶斯信念网络（Bayesian Belief Network (BBN)）
• 贝叶斯网络（Bayesian Network (BN)）

优点：

• 快速、易于训练、给出了它们所需的资源能带来良好的表现

缺点：

• 如果输入变量是相关的，则会出现问题

关联规则学习算法（Association Rule Learning Algorithms）

关联规则学习方法能够提取出对数据中的变量之间的关系的最佳解释。比如说一家超市的销售数据中存在规则 {洋葱，土豆}=> {汉堡}，那说明当一位客户同时购买了洋葱和土豆的时候，他很有可能还会购买汉堡肉。

例子：

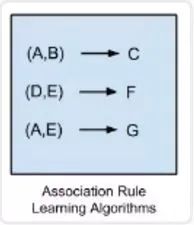
• Apriori 算法（Apriori algorithm）
• Eclat 算法（Eclat algorithm）
• FP-growth

图模型（Graphical Models）

图模型或概率图模型（PGM/probabilistic graphical model）是一种概率模型，一个图（graph）可以通过其表示随机变量之间的条件依赖结构（conditional dependence structure）。

例子：

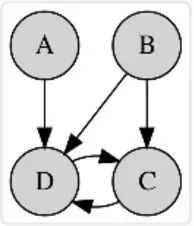
• 贝叶斯网络（Bayesian network）
• 马尔可夫随机域（Markov random field）
• 链图（Chain Graphs）
• 祖先图（Ancestral graph）

优点：

• 模型清晰，能被直观地理解

缺点：

• 确定其依赖的拓扑很困难，有时候也很模糊
  
  

end

下载1：OpenCV-Contrib扩展模块中文版教程

在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。

下载2：Python视觉实战项目52讲

在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲

在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~