【机器学习基础】深入理解Logistic Loss与回归树
Logistic Function
Logistic Function最常见的定义形式如下:
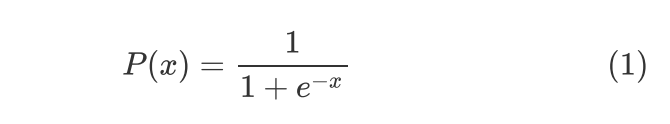
其中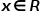 ,
, ,实际上这个公式起源于伯努利分布,
,实际上这个公式起源于伯努利分布,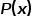 代表概率,关于其起源在此暂不赘述。
代表概率,关于其起源在此暂不赘述。
公式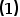 有一个重要的性质,即:
有一个重要的性质,即:
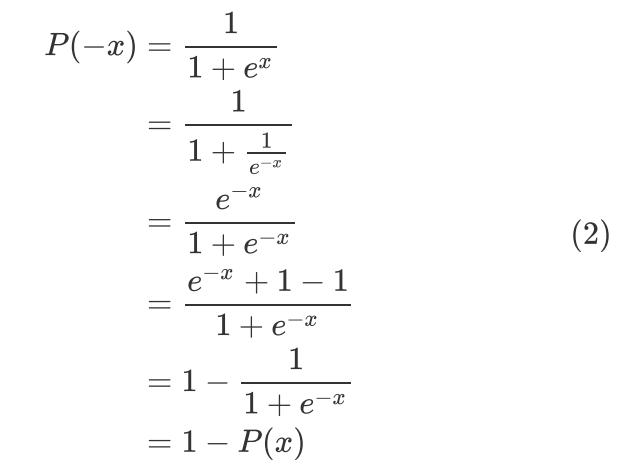
并且公式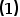 的形式在逻辑回归二分类中被广泛应用,其中
的形式在逻辑回归二分类中被广泛应用,其中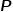 通常代表预测样本属于正例的概率。假设
通常代表预测样本属于正例的概率。假设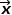 代表由多个特征组成的样本向量,
代表由多个特征组成的样本向量,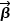 代表由每个特征的系数构成的向量,
代表由每个特征的系数构成的向量,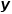 代表样本的类别标记,
代表样本的类别标记,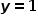 代表正例,
代表正例,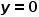 代表反例,则
代表反例,则
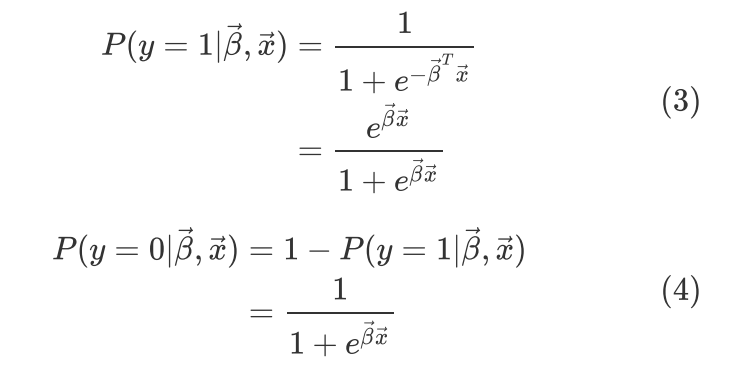
如果反例标记用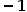 表示,则预测正例样本的公式和预测反例样本的公式可以集成为一个公式:
表示,则预测正例样本的公式和预测反例样本的公式可以集成为一个公式: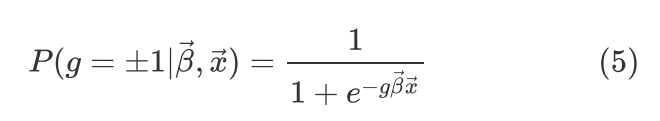
其中g = 1代表正例,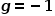 代表反例。
代表反例。
二进制交叉熵与Logistic Loss
假设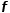 是hypothesis function,而L是loss function,训练有监督学习器的时候实际上都是如下的优化问题:
是hypothesis function,而L是loss function,训练有监督学习器的时候实际上都是如下的优化问题:
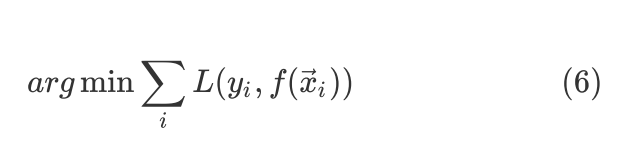
我们已经知道如果是二分类器的话,且输出是概率形式,那么我们可以选择二进制交叉熵来作为loss function,比如假设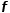 就是logistic function
就是logistic function
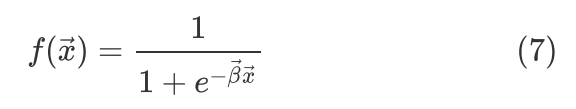
用二进制交叉熵作为loss function,正例标记为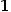 ,反例标记为
,反例标记为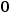 ,则
,则
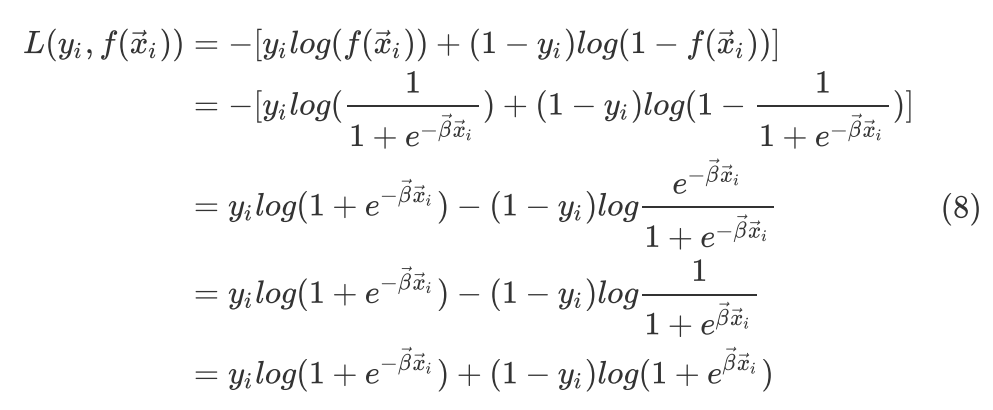
假设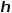 是另外一个hypothesis function,且
是另外一个hypothesis function,且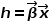 ,把
,把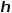 带入
带入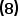 式可以得到
式可以得到
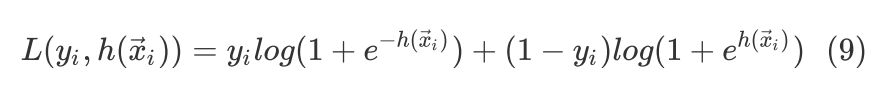
显然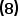 式和
式和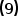 式是等价的,即
式是等价的,即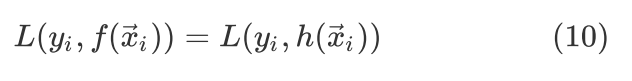
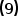 式的Loss形式叫作针对
式的Loss形式叫作针对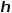 的Logistic Loss,也就是说针对
的Logistic Loss,也就是说针对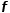 的二进制交叉熵损失等价于针对
的二进制交叉熵损失等价于针对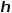 的Logistic损失,而
的Logistic损失,而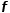 实际上是
实际上是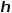 通过Logistic function的映射,即
通过Logistic function的映射,即
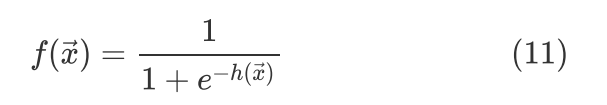
也就是说不论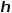 这个hypothesis function是什么形式,针对
这个hypothesis function是什么形式,针对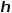 使用Logistic Loss就可以用于二分类问题,因为针对
使用Logistic Loss就可以用于二分类问题,因为针对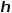 使用Logistic Loss就等价于针对
使用Logistic Loss就等价于针对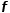 使用二进制交叉熵损失。
使用二进制交叉熵损失。
如果是用于二分类的深层神经网络,这里的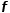 则可以看成是神经网络的最后一个Sigmoid输出神经元,如果
则可以看成是神经网络的最后一个Sigmoid输出神经元,如果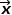 仍然看作是原始输入样本的话,则
仍然看作是原始输入样本的话,则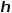 可以看成是从输入层到最后一个隐层整体构成的复合函数。
可以看成是从输入层到最后一个隐层整体构成的复合函数。
著名的梯度提升机(GBM, Gradient Boosting Machine)实际上可以对任何学习器进行Boosting操作,Boosting是一种集成学习方法,已经证明任何弱学习器都有提升为强学习器的潜能,因此Boosting通常指把弱学习器提升为强学习器的提升方法。另外,这里的Gradient是指Gradient Descent,不是中文字面意思的“梯度值提升”,“提升”是指Boosting这种集成学习范式。
GBM最常见的是GBDT(Gradient Boosting Decision Tree),因为GBDT实际上用的是基于CART中的回归树的加性模型,所以GBDT也常叫作GBRT(Gradient Boosting Regression Tree),也就是说GBDT中的弱学习器是经典的Breiman的CART中的Regression Tree,我们知道GBDT既可以用于回归也可以用于分类,那么回归树是如何用于分类的呢?
这里只讨论二分类的情况,多分类情况暂不赘述。由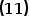 式知道如果
式知道如果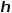 就是回归树的hypothesis function,也就是说
就是回归树的hypothesis function,也就是说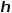 就是回归树的叶子结点的输出,那么通过Logistic function映射成
就是回归树的叶子结点的输出,那么通过Logistic function映射成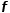 后再对
后再对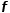 使用二进制交叉熵损失就可以做二分类任务了,由
使用二进制交叉熵损失就可以做二分类任务了,由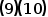 式知道也就是说直接对回归树
式知道也就是说直接对回归树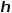 使用Logistic Loss就可以做二分类任务了。
使用Logistic Loss就可以做二分类任务了。
回归树回归分类原理
CART(Classification and Regression Tree)是最早由Breiman等人提出的一类决策树算法,其中Classification Tree使用基尼系数作为分裂准则,在此暂不赘述分类树细节,Regression Tree采用启发式算法寻找最优分裂节点,这里推导一下Loss function分别采用Squared Loss和Logistic Loss的回归和分类的数学原理。
采用Squared Loss的回归树回归
关于CART回归树的原理推导可以参考李航的《统计学习方法》,我这里试图用更通俗易懂,更详细严谨的方式进行解读和推导。
首先假设hypothesis function为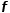 ,也即回归树为
,也即回归树为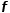 ,样本向量为
,样本向量为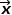 ,
,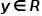 是样本
是样本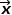 的真实target值,则回归树
的真实target值,则回归树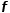 的回归预测公式为
的回归预测公式为

其中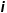 为样本编号,
为样本编号,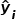 为回归树第
为回归树第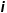 个样本的估计值。
个样本的估计值。
Squared Loss形式记为
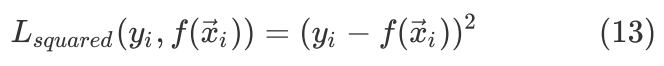
其中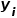 为样本编号为
为样本编号为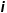 的真实target值。
的真实target值。
CART回归树为二叉树,其关键在于如何在特征空间中选择最优分裂节点进行多次二分叉分裂。用表格的形式更容易进行通俗易懂的解释,为了严谨这里先对张量的概念做一个通俗易懂的理解。
通俗理解张量:向量是一维张量,矩阵(表格)是二维张量,而像魔方那样每个小方块代表一个数据,所有数据存储在一个“三维”空间中的是三维张量(比如三通道的RGB彩色图片),当然还有更高维的张量,在各种编程语言中就对应着高维数组,实际上在物理学中对张量有严格的定义,由于其概念过于抽象,这里暂不赘述。
现在假设训练数据都存放在一张二维表格中,这里的“二维”指张量的二维。假设表格有 列,
列,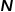 行,前
行,前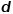 列为特征,最后一列为target
列为特征,最后一列为target 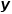 ,每一行的前
,每一行的前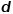 列构成
列构成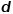 维样本向量
维样本向量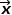 ,前
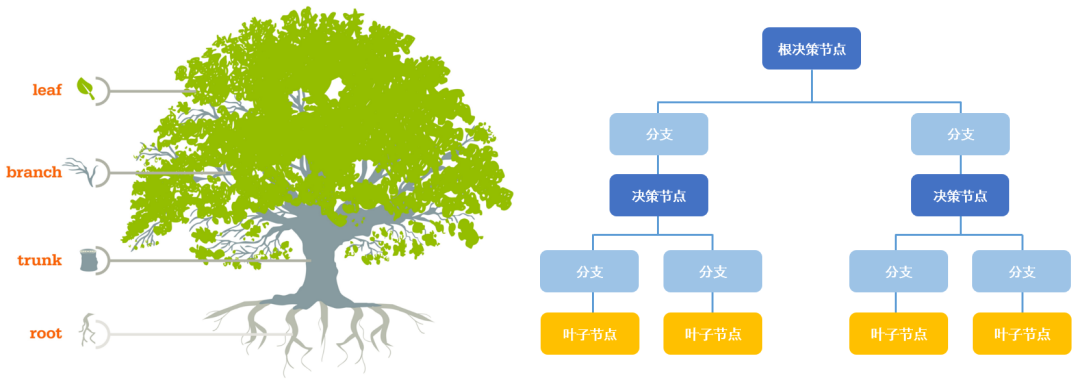
,前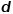 列所有数据叫作特征空间(输入空间),最后一列叫作输出空间。回归树用启发式方法在特征空间中寻找最优分裂节点对表格进行多次划分,意思就是遍历每个特征的取值,根据每个特征的取值作为判断依据(分裂节点)把表格一分为二,一分为二后的两份表格的这个特征的所有取值要么都大于等于这个判断依据(分裂节点),要么都小于等于这个判断依据(分裂节点)。第一次把原始表格进行一分为二划分的节点叫作根(root)节点,后面用同样的方法把“子表格”进行划分的节点都叫中间节点。那么如何判断哪个特征的哪个值是当前的最优分裂节点?
列所有数据叫作特征空间(输入空间),最后一列叫作输出空间。回归树用启发式方法在特征空间中寻找最优分裂节点对表格进行多次划分,意思就是遍历每个特征的取值,根据每个特征的取值作为判断依据(分裂节点)把表格一分为二,一分为二后的两份表格的这个特征的所有取值要么都大于等于这个判断依据(分裂节点),要么都小于等于这个判断依据(分裂节点)。第一次把原始表格进行一分为二划分的节点叫作根(root)节点,后面用同样的方法把“子表格”进行划分的节点都叫中间节点。那么如何判断哪个特征的哪个值是当前的最优分裂节点?
我们知道原始表格最终一定会被划分成多个子表格,每个子表格实际上是由多个判据值(分裂节点)所构成的规则下的样本的集合,这些样本同属一类,高度相似,因此可以假设每个子表格里(也就是符合这套规则的所有样本)的所有样本对应同一个估计值 ,假设最终总子表格数为
,假设最终总子表格数为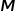 ,用
,用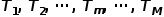 代表相应的子表格(样本集合),相应的估计值就为
代表相应的子表格(样本集合),相应的估计值就为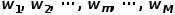 ,也即
,也即
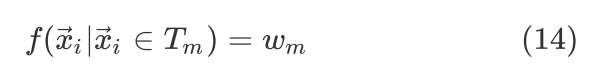
也就是说回归树的hypothesis function为
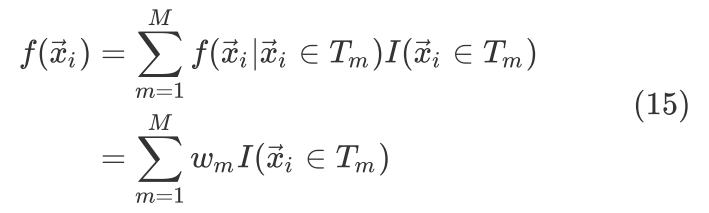
其中
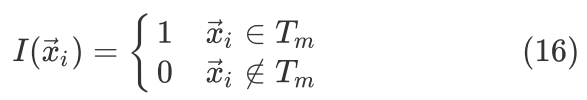
根据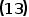 式最小化Squared Loss
式最小化Squared Loss

令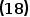 式等于
式等于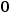 ,有
,有
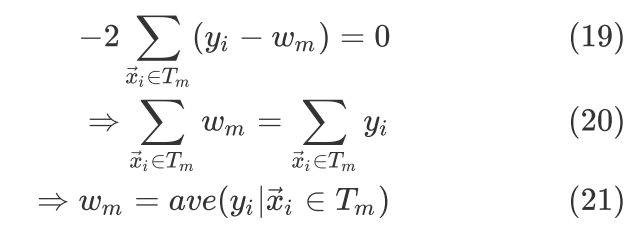
由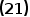 式知道在Squared Loss下每个
式知道在Squared Loss下每个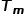 内部的最优估计值就是
内部的最优估计值就是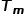 内部所有样本对应
内部所有样本对应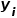 的平均值。那么每一次分裂要如何选择最优分裂节点并一步步迭代呢?
的平均值。那么每一次分裂要如何选择最优分裂节点并一步步迭代呢?
我们已经知道每一次分裂相当于把表格一分为二,并且已经知道了在Squared Loss下分裂之后每个子表格对应的估计值取子表格内部所有样本对应的target值的平均值就可以使得子表格内部的Squared Loss最小,也就是说只要每次分裂后的两个子表格的最小Squared Loss值相加最小即可,采用的方法就是遍历每个特征及其每一个取值,尝试把每一个特征下的具体的值作为分裂节点,分裂成两个子表格后计算两个子表格的最小Squared Loss的和,如果这个和在遍历了所有可能的分裂节点后是最小的,那么这一次分裂就选当前的分裂节点。
具体地,假设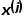 是第
是第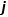 个特征,
个特征,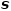 是特征
是特征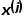 的某个取值,把
的某个取值,把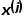 和
和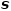 分别作为切分变量和切分点,则可以把当前表格切分成如下两个表格:
分别作为切分变量和切分点,则可以把当前表格切分成如下两个表格:
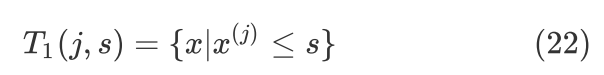
和
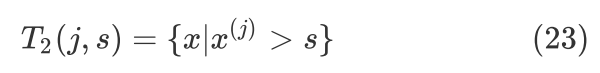
计算下式寻找最优切分变量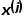 和最优切分点
和最优切分点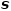 ,
,
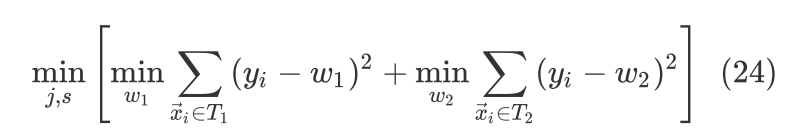
由(21)式可以知道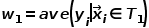 和
和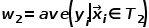 时可以使得
时可以使得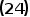 式在当前分裂点最小,也就是说只要遍历所有可能的分裂点(j,s),找到全局最小的
式在当前分裂点最小,也就是说只要遍历所有可能的分裂点(j,s),找到全局最小的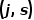 即可。后续每一次表格的一分为二都采取同样的方法,直到满足停止条件。采用Squared Loss的回归树也叫最小二乘回归树。
即可。后续每一次表格的一分为二都采取同样的方法,直到满足停止条件。采用Squared Loss的回归树也叫最小二乘回归树。
采用Logistic Loss的回归树二分类
由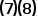 式已经知道了Logistic Loss由Logistic function和Binary Entropy Loss推导而来,而Logistic function也叫Sigmoid function,所以Logistic Loss也叫Sigmoid Binary Entropy Loss,它可以把回归模型用于二分类任务。
式已经知道了Logistic Loss由Logistic function和Binary Entropy Loss推导而来,而Logistic function也叫Sigmoid function,所以Logistic Loss也叫Sigmoid Binary Entropy Loss,它可以把回归模型用于二分类任务。
Logistic Loss最常用的形式是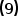 式的label
式的label 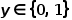 的形式,如果label
的形式,如果label 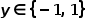 ,则其形态为
,则其形态为
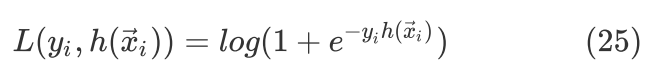
在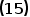 式中已经知道了回归树的hypothesis function,这里尝试采用Logistic Loss作为loss function来推导其训练过程。以下推导Logistic Loss采用
式中已经知道了回归树的hypothesis function,这里尝试采用Logistic Loss作为loss function来推导其训练过程。以下推导Logistic Loss采用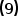 式的形态,所以取label
式的形态,所以取label 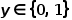 。那么训练分类器也就是如下的优化问题
。那么训练分类器也就是如下的优化问题
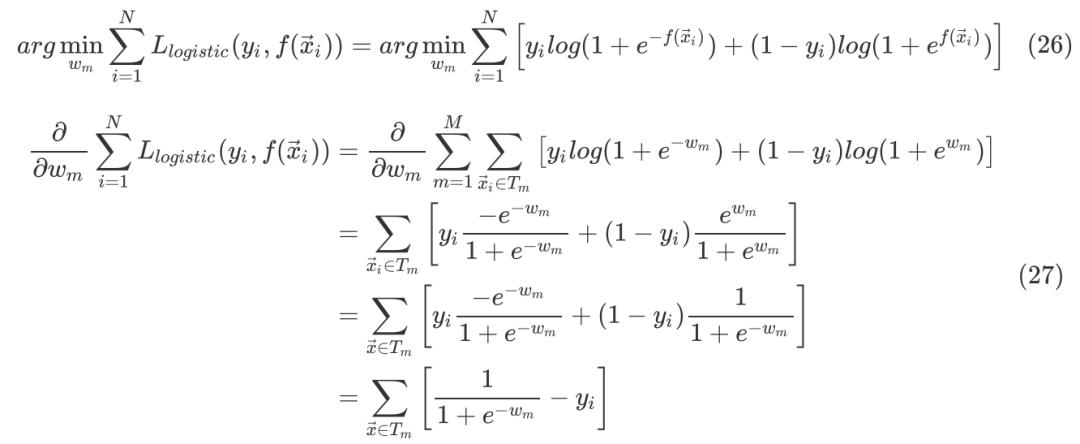
令(27)式等于0,则
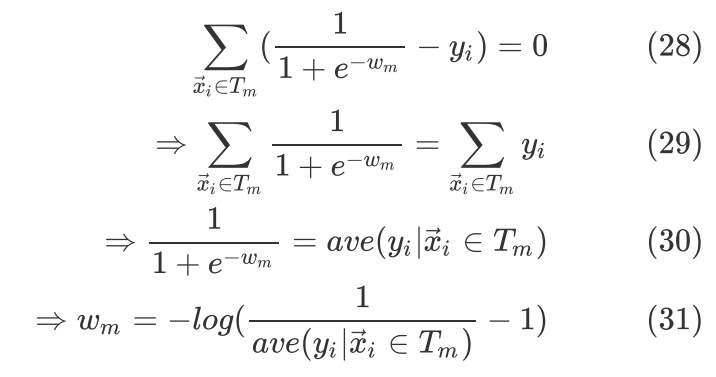
分裂思想与前述的最小二乘回归树一样,只不过Loss采用Logistic loss,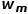 采用(31)式的计算值。实际上由(30)式已经可以看出回归树的每个叶节点的权值都输入Logistic function把输出值映射到(0,1)后的值就是
采用(31)式的计算值。实际上由(30)式已经可以看出回归树的每个叶节点的权值都输入Logistic function把输出值映射到(0,1)后的值就是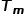 里面
里面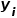 的均值。
的均值。
往期精彩回顾
本站qq群704220115,加入微信群请扫码:
