扛鼎之作！Twitter 图机器学习大牛发表160页论文：以几何学视角统一深度学习
共 4942字，需浏览 10分钟
·
2021-05-05 08:22
大数据文摘授权转载自AI科技评论
作者：Michael Bronstein
编译：Mr Bear、青暮
导语：近日，帝国理工学院教授、Twitter 首席科学家 Michael Bronstein 发表了一篇长达160页的论文（或者说书籍），试图从对称性和不变性的视角从几何上统一CNNs、GNNs、LSTMs、Transformers等典型架构，构建深度学习的“爱尔兰根纲领”！本文是Michael Bronstein对论文的精华介绍。
「几何深度学习」试图从对称性和不变性的视角从几何上统一多种机器学习问题。这些原理不仅为卷积神经网络的性能突破和最近大热的图神经网络奠定了基础，也提供了一种原理性的方法来构建针对具体问题的新型归纳偏置。
相关论文：
https://arxiv.org/pdf/2104.13478.pdf
1872 年 10 月，位于德国巴伐利亚城的埃尔兰根大学任命了一位年轻的教授。按照惯例，这位教授需要提出一项初始研究项目，而他提出的项目名称似乎有些乏味——「近期几何学研究的比较综述」。这位教授就是年仅 23 岁的 Felix Klein，他的这项初始工作就是数学史上鼎鼎大名的「爱尔兰根纲领」。
图注：Felix 和他的爱尔兰根纲领
19 世纪，几何学蓬勃发展，该领域的学者硕果累累。在欧氏几何提出近两千年后，彭色列首次构建了射影几何，高斯、波尔约、罗巴切夫斯基提出了双曲几何，黎曼提出了椭圆几何，这说明我们可以建立一个由各种几何学组成的完整体系。然而，这些方向迅速分化为各个独立的研究领域。于是，那个时期的许多数学家纷纷思考，不同的几何学分支相互之间有何关系，究竟应该如何「定义」几何？
Klein 突破性地提出将几何定义为对不变性的研究，即研究在某类变换下保持不变的结构（对称性）。Klein 通过群论形式化定义了这种变换，并且使用群及其子群的层次对由它们产生的不同几何进行分类。因此，刚性运动群产生了传统的欧氏几何，而仿射或射影变换分别产生了仿射几何和射影几何。值得一提的是，爱尔兰根纲领仅仅局限于齐次空间，最初并不适用于黎曼几何。
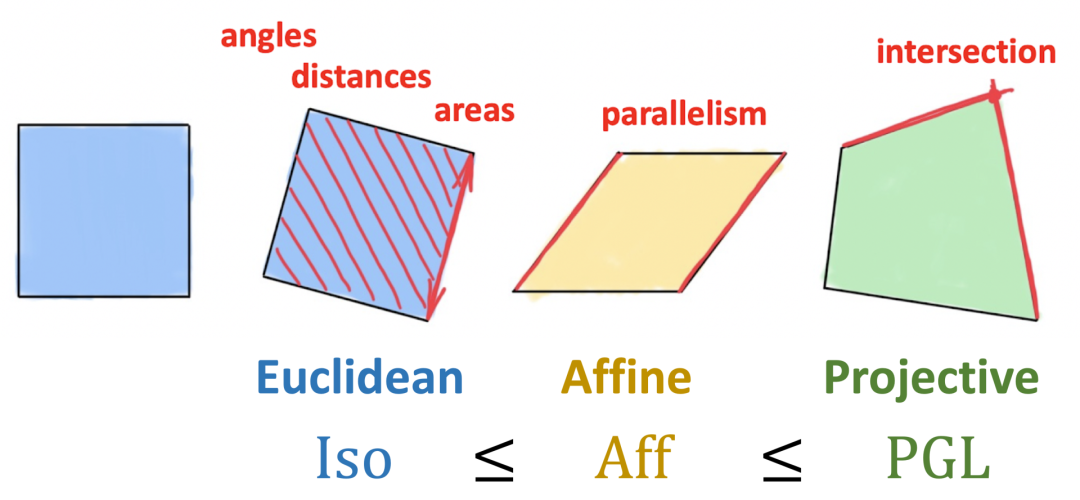
图 2：Klein 的爱尔兰根纲领将几何学定义为研究在某类变换下保持不变的性质。我们通过保持面积、距离、角度、平行结构不变的刚性变换（建模为等距群）定义 2 维欧氏几何。仿射变换将保持平行结构，但并不能保证距离或面积不变。射影变换的不变性最弱，只保持交点和交比不变，对应于以上三种变换中最大的群。因此，Klein 认为射影几何是最为通用的。
爱尔兰根纲领对几何学和数学的影响是极为深远的，其影响也延伸到了其它领域（尤其是物理学），对对称性的思考使我们可以从第一性原理出发导出守恒定律（例如，举世闻名的「诺特定理」）。数十年后，人们通过规范不变性的概念（于 1954 年由杨振宁和米尔斯提出的广义形式）证明这一基本原理成功地统一了除引力之外的所有自然基本力。这就是所谓的标准模型，它描述了我们目前所知道的所有物理知识。
正如诺贝尔奖获得者、物理学家 Philip Anderson 所言：
“it is only slightly overstating the case to say that physics is the study of symmetry.’’ 稍显夸张地说，物理学就是对对称性的研究。
我们认为，当下的深度（表征）学习研究领域的情况与 19 世纪的几何学研究是相似的：一方面，深度学习在过去十年间为数据科学领域带来了一场革命，它使许多之前被认为无法实现的任务成为了可能——无论是计算机视觉、语音识别、自然语言翻译或围棋游戏中都是如此。另一方面，我们现在拥有了各种适用于不同数据的神经网络架构，但是却很少发展出统一的原理。因此，我们很难理解不同方法之间的关系，这不可避免地使我们对相同的概念进行重复开发。
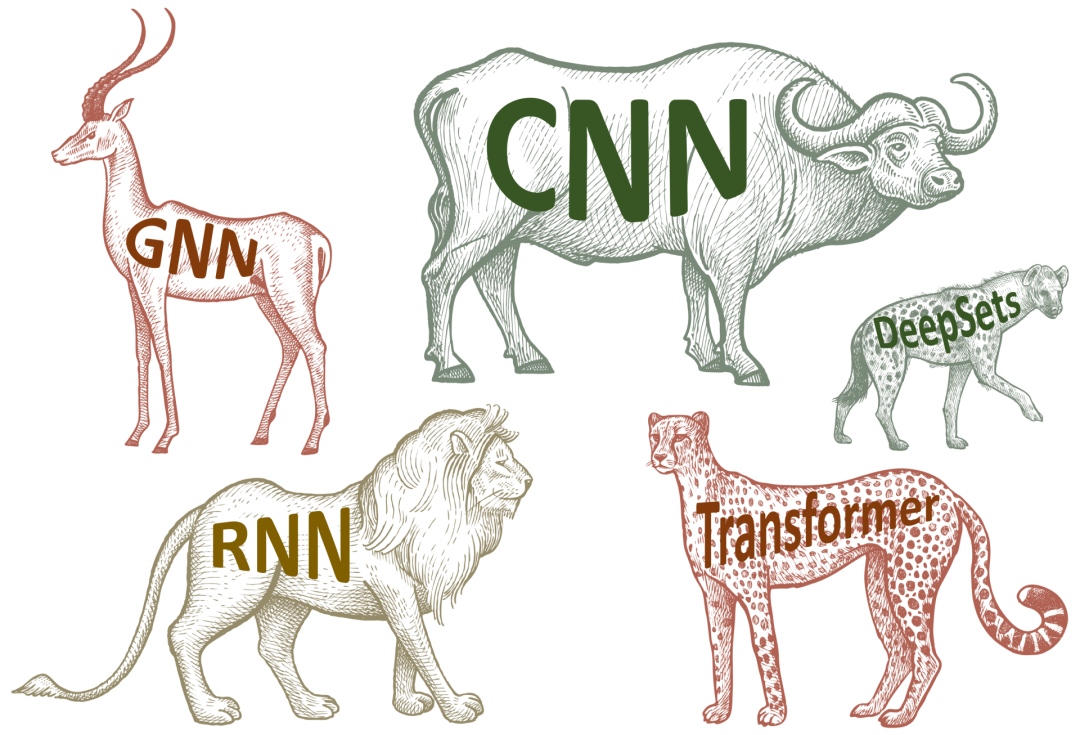
图注：现代的深度学习——有各种各样的架构，但是缺乏统一的原理。
与 Klein 的爱尔兰根纲领相类似，Michael Bronstein 等人在论文「Geometric deep learning: going beyond Euclidean data」（https://arxiv.org/abs/1611.08097）中引入了「几何深度学习」的概念，作为近期从几何学的角度将机器学习统一起来的尝试的总称。这样做有两个目的：首先，它提出了一个通用的数学框架，从而推导出当下最成功的神经网络架构；其次，它给出了一种有建设性的过程，以一种有条理的方法构建未来的框架。
在最简单的情况下，有监督机器学习本质上是一个函数估计问题：在训练集（例如，带有标签的狗和猫的图片）上给定某些未知函数的输出，试图从某些假设函数类别中找到一个函数 f，该函数可以很好地拟合训练数据，使模型可以预测出先前未见过的输入对应的输出。在过去的十年间，以 ImageNet 为代表的大型、高质量数据集和不增长的计算资源（GPU）使我们可以设计各种可以被用于此类大型数据集的函数。
神经网路似乎可以很好地表征函数，即使是感知机这种自建单的架构也可以在仅仅使用两层网络的情况下生成各类函数，它可以使我们以理想的准确率近似任意连续函数——该性质被称为「通用近似」（又称万能近似定理）。
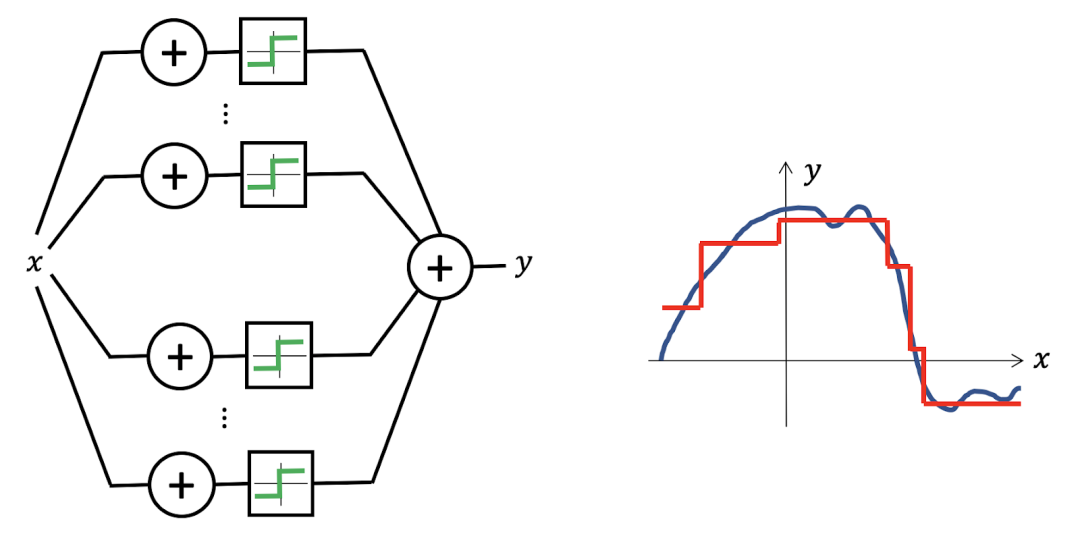
图注：多层感知机是一种只包含一个隐层的通用近似器。他们可以表征阶跃函数的组合，从而以任意的精度近似任意的连续函数。
在低维空间中，该问题是近似理论中的一类已经被广泛研究的经典问题，从数学上对估计误差由精确的控制。但是在高维空间中，情况就完全不同了：显然，即使为了近似一类简单的函数（例如，李普希兹连续函数），样本数会随着维度呈指数增长，该现象被称为「维数诅咒」。由于现代机器学习方法需要处理具有数千甚至数百万个维度的数据，维数诅咒往往是存在的，使我们无法通过朴素的方式进行学习。
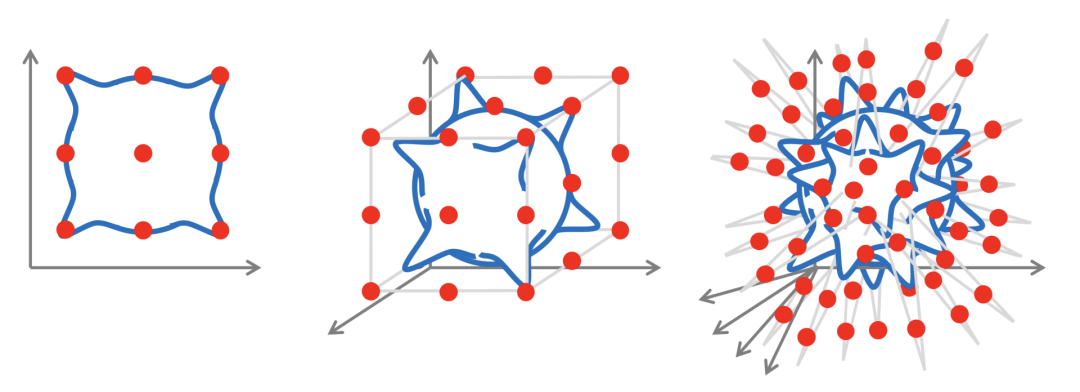
图注：维数诅咒示意图。对于一个由处于 d 维单位超立方体的象限中的高斯核组成的连续函数（蓝色），如果我们希望以 ε 的误差近似一个李普希兹连续的函数，则需要 𝒪(1/εᵈ) 的样本（红色点）。
在计算机视觉问题（例如，图像分类）中，这种现象尤为突出。即使是很小的图像也往往具有非常高的维度，但是直观地看，当我们将一张图像解析为一个输入给感知机的向量时，许多图像的结构被破坏并丢弃了。即使我们将图像仅仅平移一个像素，向量化的输入也会有很大的区别。为了使平移后的输入能够被分到同一类中，我们需要向神经网络输入大量的训练样本。
幸运的是，在许多高维机器学习问题中，我们可以使用来自于输入信号的几何学上的额外结构信息。我们将这种结构称为「对称先验」，这种通用的强大原理有助于我们应对维数诅咒问题。在图像分类的例子中，输入图像 x 不仅仅是一个 d 维向量，也是一个在某个域 Ω 上定义的信号，在本例中这个域是一个二维网格。我们通过一个对称群 𝔊（本例中为一个二维变换组成的群）捕获域的结构信息，该群在域中的点上进行操作。在信号 𝒳(Ω) 的空间中，底层域上的群操作（群的元素，𝔤∈𝔊）通过群表征 ρ(𝔤) 体现。在本例中，上述操作为简单的平移操作，即一个在 d 维向量上运算的 d×d 矩阵。
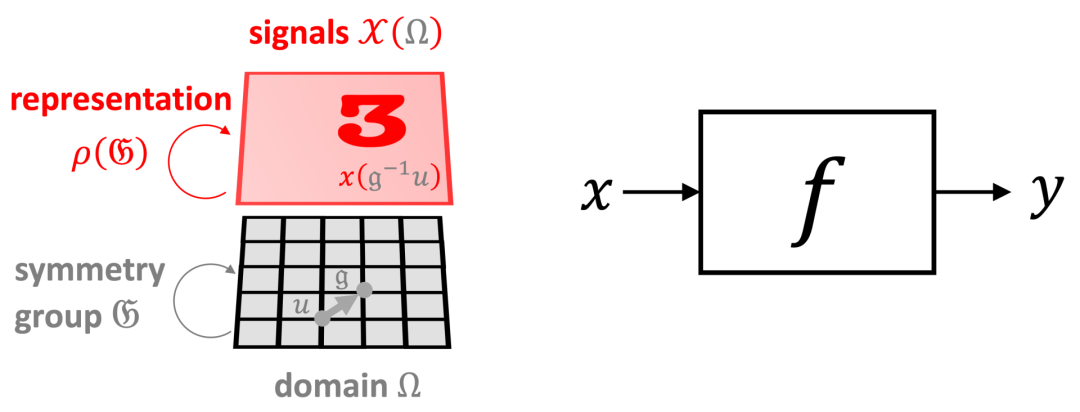
图注：几何先验示意图——我们在域(网格 Ω)上定义输入信号(图像 x∈𝒳(Ω))，其中的对称群（变换群 𝔊）通过群表征ρ(𝔤) 在信号空间中进行平移操作。对函数（例如，图像分类器）如何与群进行交互的假设限制了假设类别。
输入信号底层的域的几何结构为我们试图学习的函数 f 的类别施加了架构信息。对于任意的 𝔤∈𝔊 和 x，我们可以找出不会被群的操作所影响的不变性函数，即 f(ρ(𝔤)x)=f(x)。另一方面，有时函数具有相同的输入输出结构，并且输出以与输入相同的方式进行变换，这种函数被称为同变性函数，它满足 f(ρ(𝔤)x)=ρ(𝔤)f(x)。
在计算机视觉领域中，图像分类是一种典型的人们希望得到不变性函数的任务（例如，无论猫位于图像的什么位置，我们都希望将该图分类为猫）；而图像分割任务的输出是一个像素级别的标签掩模，这是一种同变性函数（分割掩模需要遵循输入图像的变化）。
「尺度分离」是另一种强大的几何先验。在某些情况下，我们可以通过「同化」附近的点来构建域的多尺度层次结构（如图7 所示的 Ω and Ω’），并且生成一个由粗粒度算子 P 关联的信号空间的层次。在粗尺度上，我们可以应用粗尺度的函数。如果一个函数 f 可以被近似为粗粒度算子 P 和粗尺度函数的组合 f≈f’∘P，则 f 是局部稳定的。尽管 f 可能取决于长距离依赖，如果 f 是局部稳定的，它们可以被分解为局部交互，然后向着粗尺度传播。
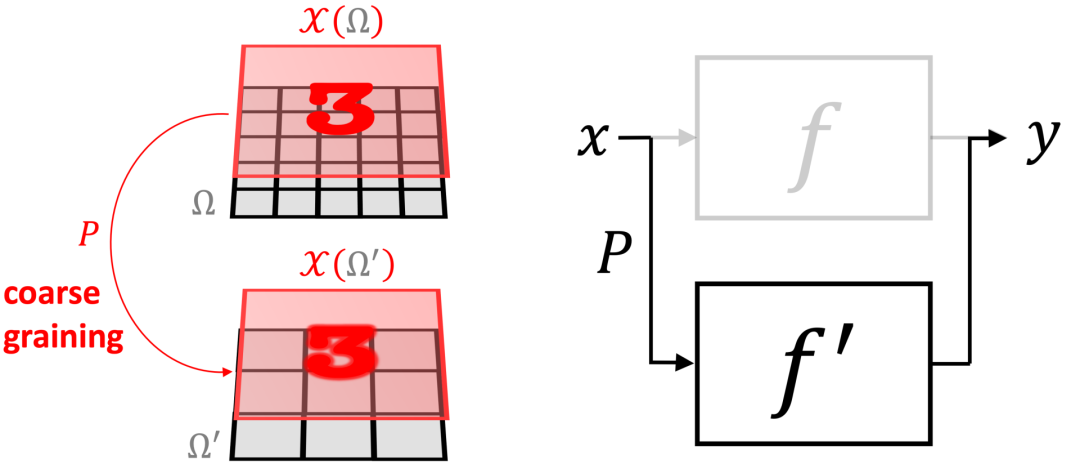
图注：尺度分离的示意图，其中我们可以将细尺度函数 f 近似为粗尺度函数 f' 和粗粒度算子 P 的组合 f≈f′∘P
这两个原理为我们提供了一个非常通用的几何深度学习设计范式，可以在大多数用于表示学习的流行深度神经架构中得以体现：一个典型的设计由一系列同变层（例如，CNN 中的卷积层）组成，然后可以通过不变的全局池化层将所有内容聚合到一个输出中。在某些情况下，也可以通过采用局部池化形式的粗化过程（coarsening procedure）来创建域的层次结构。
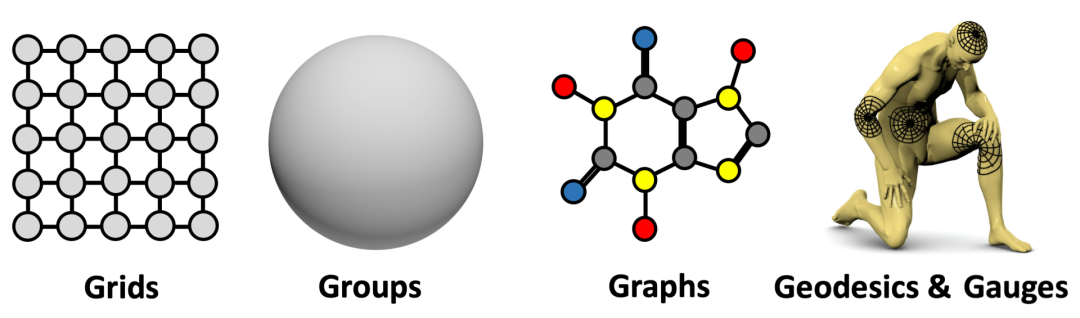
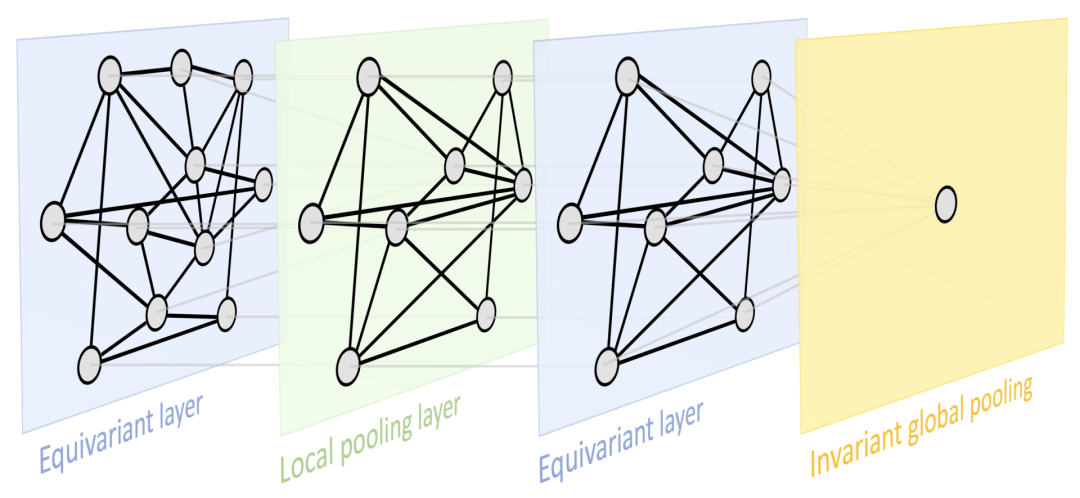图注：展示了一种非常通用的设计，可以应用于不同类型的几何结构（例如，网格，具有全局变换群的齐次空间，图（集合也是其中一种特例）和流形，这些结构具有全局等距不变性和局部规范对称性。基于上述原理，我们实现了目前深度学习领域中的一些最流行的架构：由平移对称导出的卷积网络（CNN），由置换不变性导出的图神经网络、DeepSets 和 Transformer，由时间扭曲不变性导出的门控 RNN（例如 LSTM 网络），以及由规范对称性导出的计算机图形和视觉中使用的 Intrinsic Mesh CNN。
这是一种非常通用的设计，可以应用于不同类型的几何结构，例如网格，具有全局变换群的齐次空间，图形（以及特定情况下的集合）和流形，这些结构具有全局等距不变性和局部规范的对称性。这些原理的实现带来了目前深度学习中的一些最流行的架构：由平移对称导出的卷积网络（CNN），由置换不变性导出的图神经网络、DeepSets和Transformers，由时间扭曲不变性导出的门控RNN（例如LSTM网络），以及由规范对称性导出的计算机图形和视觉中使用的Intrinsic Mesh CNN。
最后还要重点强调的是，对称性在历史上是众多科学领域中的一个关键概念。在机器学习研究社区中，对称性的重要性早已得到普遍认可，特别是在模式识别和计算机视觉的应用中，关于等变特征检测（Equivariant Feature Detection）的研究最早可以追溯到shun'ichi Amari 和Reiner Lenz 等人的工作。在神经网络的研究历史中，Marvin Minsky 和 Seymour Papert 提出的感知器群不变性定理（The Group Invariance Theorem）对（单层）感知器学习不变性的能力提出了基本限制。这是研究多层架构的主要动机之一，并最终催生了深度学习。
相关链接：
