计算机中有哪些令人拍案叫绝的设计?
大家好!
前天日本前首相安倍晋三在演讲过程中遇刺,这可能会成为2022年世界政坛上最热门的一个新闻,但是随后美国居然下半旗哀悼这位「盟友」,让人想起难道美国忘记了八十年前那场偷袭了吗?网上也是众说纷纭,但是咱不太关心政治,今天咱们谈论的话题跟政坛也没有关系,但是今天这篇文章就从那场偷袭使用的飞机开始吧。
那场偷袭早在2001年已经被拍摄成了电影——《珍珠港》,绝对是一部精彩的空战电影。但是在观影的过程中,你有没有想过这个问题:二战时期的飞机,在进行空战过程中自己飞机射出的子弹难道不会击中自己飞机的桨叶吗?其实我小时候看这部电影就有这样的疑问,直到后来我在大学学习了《机械原理》后,解其背后的原理后:

机枪射击协调器:它是一战中在盟军中服役的荷兰人安东尼·福克发明的,他把凸轮安装在螺旋桨轴上面,凸轮的三个凸起与桨叶刚好错开一个角度,当突起部分碰到金属棒后,金属棒后端连接的机枪发射装置就会被激活,继而完成子弹发射,反之,当桨叶与枪管形成一条直线时,机枪自动停止射击。这个巧妙的设计完美地避开了战斗机出现自残的事故。
当时我知道它的原理后,反应是这样的:
卧槽,还有这种操作!
卧槽,这么简单我怎么没想到!
的确,让人虎躯一震的发明往往看上去都非常简单,而且你经常会想,这么简单,嗯,我怎么没想到?
我还是那句话,简单即是美,但是简单往往比复杂困难得多。
其实计算机的设计也是一门艺术的博弈,我们今天聊的话题就是计算机补码的运算,它看似简单,但是这个设计也是精妙绝伦。
一,逻辑电路是如何计算加法的
1938年,香农(这个人不用说了吧,计算机行业的人没人没听过他吧)在麻省理工学院发表了那篇题为《继电器和开关电路的符号分析》(A Symbolic Analysis of Relay and Switching Circuits)的著名硕士论文,这是一篇具有划时代意义的论文,他在文中清晰地阐述:电子工程师可以运用布尔代数的所有工具去设计开关电路。也就是说逻辑运算居然可以用电路来进行实现,随后人们根据这一理论设计出了各种逻辑门(Logic Gate)来进行数据运算,后期的电子计算机的运算原理都是基于这一理论进行实现的,比如人们根据继电器或者晶体管的特性,设计了异或门(关于异或运算的本质请参考 如何通俗理解异或运算 ):
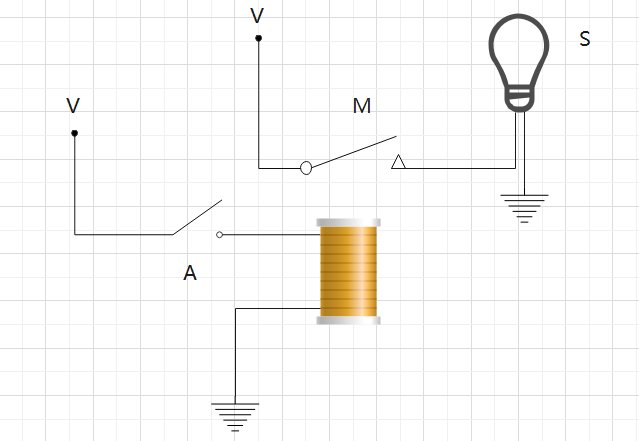
当开关 A 闭合,线圈产生磁性将开关 M 吸合,接通灯泡的回路,灯泡就会亮,这是一个最简单的逻辑回路。你能想象人类发明CPU甚至所有的存储设备其实就是这一堆堆开关组合成的吗,虽然现代CPU用的是晶体管(速度更快、体积更小),但是原理都是一样的。比如苹果最新发布的M2芯片上面集成了200亿个晶体管,翻译成人话就是上面放了200亿个开关。
这就像咱们老祖宗说的那句话,一生二,二生三,三生万物。
后来人们根据上面那个电路进行简单改造,无非就是开关的常开变常闭,或者常闭变常开等等,发明出了各种不同的逻辑门,可以实现更多的逻辑回路,比如与门(AND)、与非门(NAND)、或门(OR)、或非门(NOR)、异或门(XOR)等等。
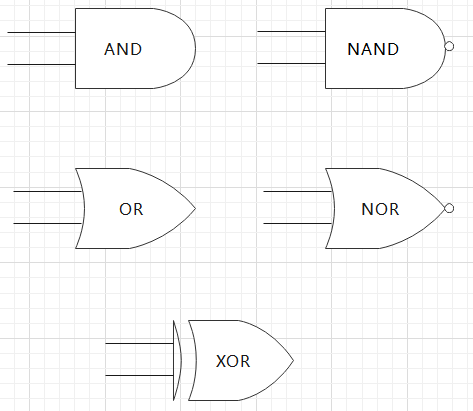
比如下面这个与门就是连个开关A与B必须同时闭合灯泡才能亮:
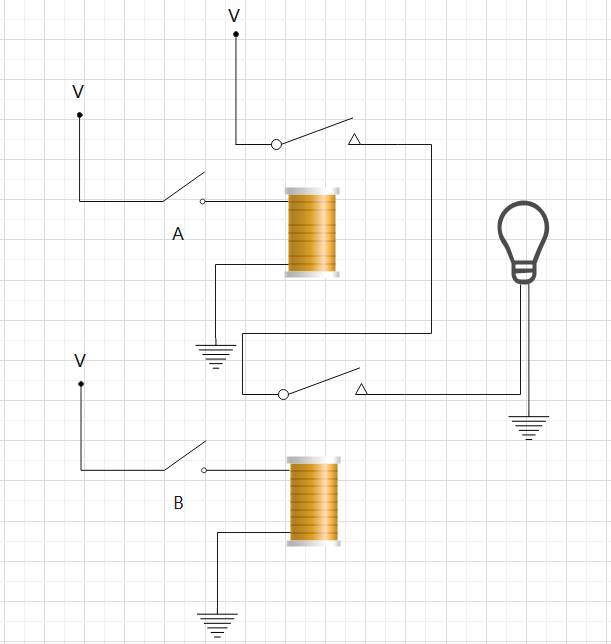
这样的电路人们没想到居然会与二进制的加法存在着某些联系,比如二进制1+1=10的进位是1,而这个与门电路双开关必须同时闭合才会亮,如果闭合代表1,断开代表2,那么逻辑关系就是1 AND 1 = 1.
有一天,人们惊奇地发现,一个异或门并联一个与门居然能做简单的二进制位的加法运算,给它命名叫半加器。之所以叫半加器,是因为它还没有办法将进位的输出纳入下一位的运算,比如 1+1=10,等号右边的进位暂时还不能纳入下一位的运算。
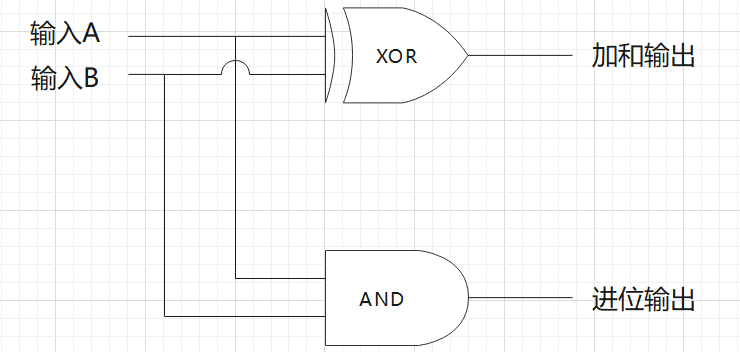
我们把这一堆符号合成一个整体:

半加器
后来,人们改进了这个电路,用两个半加器再加一个或门,组成一个全加器,这次就厉害了,全加器弥补了半加器不能计算让进位参与运算的缺点,可以将前一位的进位纳入本位进行一块计算,所以全加器输入端有三个输入:
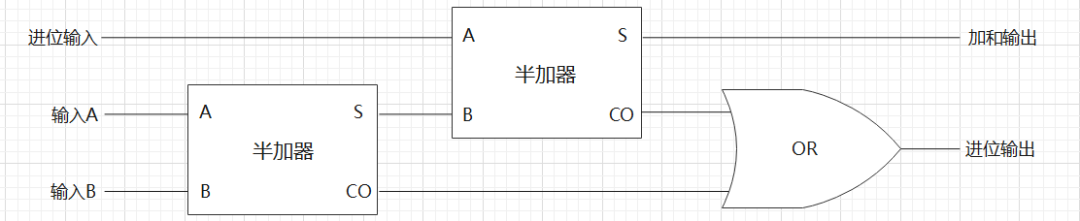
我们把上面这一堆符号合成一个整体:

全加器
多个全加器组合在一块就能计算多位的二进制加法,下面这组加法器就能计算四位二进制的加法:
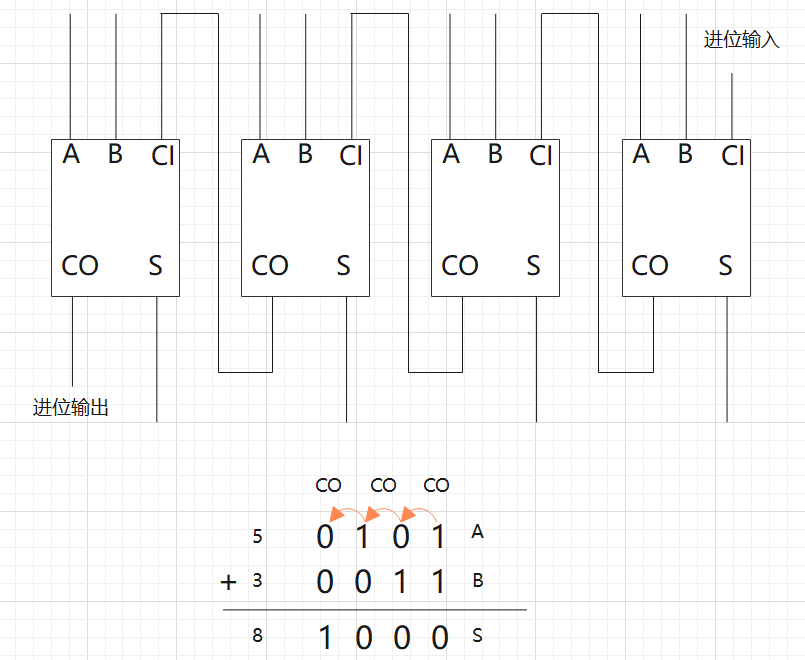
通过这组加法器的组合,我们就能计算十进制的 5+3=8 运算,很难想象,这样的运算居然是我们通过几个开关实现的!实际上这正是现代计算机进行加法计算的原理。
这里,你有没惊呼:
卧槽,还有这种操作!
卧槽,这么简单我怎么没想到!
不过先别惊讶的太早,后面还有更让你惊讶的。
到这里,我们已经能够通过我们设计的逻辑电路来计算加法了,但是还有个重要的问题:减法如何计算呢?因为计算减法涉及到借位这种繁琐的操作,而上面我们设计的电路只能进位,难道我们还要为减法设计特定的逻辑电路吗,答案肯定是否定的,那样我们的电路就会非常复杂,我们考虑的是如何通过现有的逻辑电路,也就是如何通过加法来计算减法呢?
这个问题特别有意思,有人会说了,减去一个数等于加上这个数的负数,比如 5-3=2 这个式子,可问题是这样的说法实际上还是在计算减法,按照我们目前设计的开关电路是实现不了的,那怎么办呢?
想象一下,我们上小学的时候,刚开始学习三位数的减法的时候,我们都不喜欢一些带有借位的减法,比如
我们这里用一个技巧,先用 999 减去减数 147,显然这个算式不会产生借位:
为什么这个间接的运算会正确呢?这是因为的原题目可以化成下面的运算:
到这里,你可能会有疑惑:可这个式子还用到了减法啊,而且是两次,难道计算机在计算的时候还会有技巧跳过这个减法吗?
在这里,神奇的事情发生了,由于计算机采用的是二进制,第一个减法也就是求补数是从一串1的数字中减去的,而二进制求补的运算不像十进制那样,前者根本不需要做减法,而是将原来二进制中的数字1变为0, 0变为1即可(这与直接计算减法结果是一样的,但是这个技巧对计算机来说就省下了做减法的运算),这个求相反数我们可以称为反码,可以通过逻辑电路中的反向器来实现,第二个减法在二进制中减的是最高位,而这个对计算机来说我们只需要通过一个逻辑门电路来限制最高位输出即可实现。
下面我们来看一下使用二进制计算这一过程有多奇妙
第一步,求补运算:

第二步,将结果加上被减数 213:

第三步,将第二步的结果加 1:
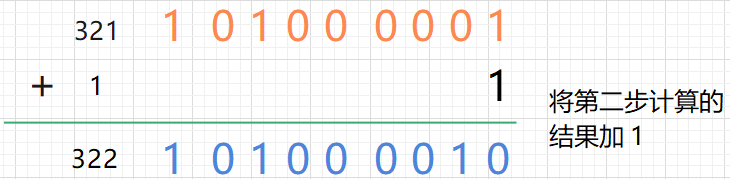
第四步,将第三步的结果最高位取反,相当于减去了256:

这样就最终得出了我们想要的结果:66,整个过程虽然采用了两次减法,但是在二进制看来,根本没有使用减法。
二,为什么采用补码来存储整数
但是,上面这个电路还有局限性,它只能计算被减数大于减数的运算,而且不能表示负数,我们想要的结果是使用现有的电路,让它能够计算加法、减法、还有负数,换句话说,让所有的运算都按照加法来实现,该如何实现呢?
这时候,补码运算就登场了。
首先,计算机为了区分整数与负数,规定了符号位,规定最高位为「符号位」,0代表正数,1代表负数,剩下的才是「数字位」。例如对于两个字节 short 类型数字 1 在计算机内部是这样表示的:

而整数 -1 的表示方法是这样的,只是符号位变为了 1:
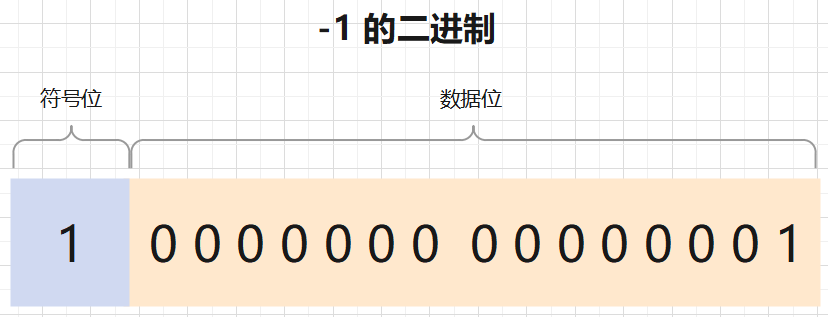
但这样做是有代价的,意味着我们数据位的表示实际上是少了一位,导致我们原本能表示的数字没那么大了。例如单字节原本能表示 0 ~ 255 之间的数字,但是因为符号位占据了 1 位,实际我们表示数据的位数变为了 7 位,最大只能表示 127.
这时候,我们引出反码还有补码这个概念:正数的反码补码都是其原码,而复数的反码比较特殊,符号位不变,数据位取反就是反码,反码加 1 就是补码:
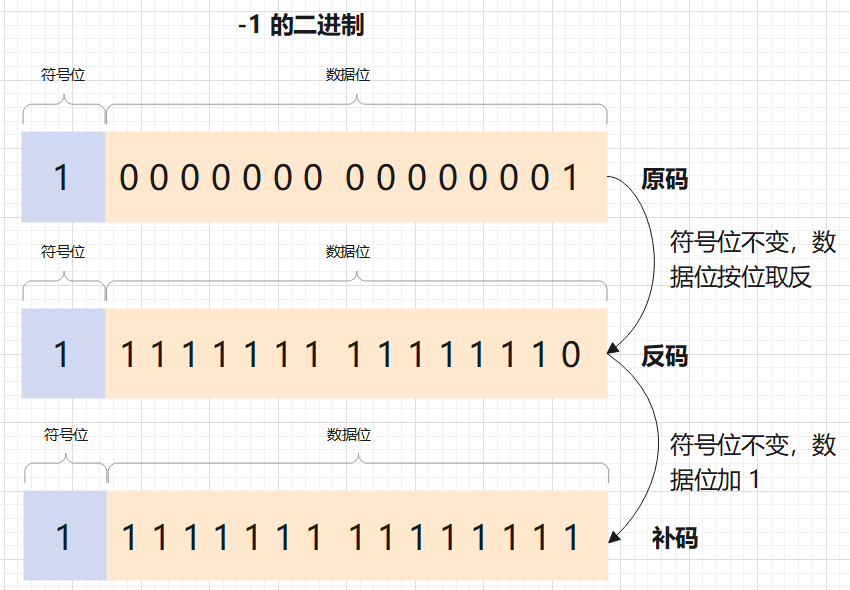
计算机内部所有的运算都采用补码的形式,那么为什么要这样呢?
我们先来看如果采用原码的形式进行计算,假设我们要计算 1 - 3,实际上就是1+(-3):

这样得出的结果竟然是 1 + (-3) = -4,结果显然是不正确的
那么如果我们采用反码进行计算,会怎样呢?

这样得出的结果就是正确的,与我们预期的一样,但是如果我们计算 3-1 会怎么样呢,再试试:

最后居然得出 3+(-1)=1 的结果,这说明采用反码运算,小数减大数没问题,但是大数减小数结果就出了问题,直觉告诉我们,结果差了1.
随后,人们想出了补码这种神奇般的操作,我们看一下它的结果是怎样的:

这样计算的结果就与我们期待的一样,是正确的。
再细品一下,为什么补码运算会正确呢,我们仔细分析一下:
当大数减去小数的时候,结果一定是正数。而之前我们采用的反码运算,结果总是少了1,如果采用补码来计算的话,负数从反码转为补码要加上1,在计算出结果后,因为正数的补码与反码相同,所以不用再减去,所以刚好相当于把结果加了1. 妙,不可言;
当小数减去大数的时候,结果一定是负数。如果采用补码运算,负数从反码转化为补码要加上1,而恰恰,结果是负数,这个负数从补码转为原码又要减去1, 刚好抵消,结果不受影响。妙,不可言。
补码的发明,彻底简化了我们的硬件电路,不必为减法设计额外的电路,让我们仅仅通过加法电路就能计算减法,真是太神奇了。
看到这里,你有没有惊呼开头那两句话:
卧槽,还有这种操作!
卧槽,这么简单我怎么没想到!
