【机器学习】Mean Shift原理及代码
Mean Shift介绍
Mean Shift (均值漂移)是基于密度的非参数聚类算法,其算法思想是假设不同簇类的数据集符合不同的概率密度分布,找到任一样本点密度增大的最快方向(最快方向的含义就是Mean Shift) ,样本密度高的区域对应于该分布的最大值,这些样本点最终会在局部密度最大值收敛,且收敛到相同局部最大值的点被认为是同一簇类的成员。
Mean Shift的原理
均值漂移聚类的目的是发现一个平滑密度的样本点。它是一种基于质心的算法,其工作原理是将质心的候选点更新为给定区域内的点的平均值。然后在后处理阶段对这些候选点进行过滤,以消除近似重复点,形成最终的一组质心。给定一个候选质心xi和迭代次数t,按照以下的等式进行更新:
Mean Shift算法的流程可被理解为:
计算每个样本的平均位移
对每个样本点进行平移
重复(1)(2),直到样本收敛
收敛到相同点的样本可被认为是同一簇类的成员
## Mean Shift算法的优缺点
不需要设置簇的个数也可以处理任意形状的簇类,同时算法需要的参数较少,且结果较为稳定不需要像K-means的样本初始化。但同时Mean Shift对于较大的特征空间需要的计算量非常大,而且如果参数设置的不好则会较大的影响结果,如果bandwidth设置的太小收敛太慢,而如果bandwidth参数设置的过大,一部分簇则会丢失。
Mean Shift的代码实现
在Sklearn中实现了MeanShift算法,其算法使用方法如下:
sklearn.cluster.MeanShift(*, bandwidth=None, seeds=None, bin_seeding=False, min_bin_freq=1, cluster_all=True, n_jobs=None, max_iter=300)
其中最主要的参数是bandwidth,这个参数是用于RBF kernel中的带宽。参数seeds是用于初始化核的种子,如果不指定则会使用sklearn.cluster.estimate_bandwidth进行估计。
使用示例:
from sklearn.cluster import MeanShift
import numpy as np
X = np.array([[1, 1], [2, 1], [1, 0],
[4, 7], [3, 5], [3, 6]])
clustering = MeanShift(bandwidth=2).fit(X)
Mean Shift的应用
# 导入相关模块和导入数据集
import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets import make_blobs
# 生成样本数据
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)
es_bandwidth = estimate_bandwidth(X,quantile=0.2, n_samples= 500)
'''
estimate_bandwidth()用于生成mean-shift窗口的尺寸,
其参数的意义为:从X中随机选取500个样本,
计算每一对样本的距离,然后选取这些距离的0.2分位数作为返回值
'''
MS = MeanShift(bandwidth=es_bandwidth)
MS.fit(X)
labels = MS.labels_
cluster_centers = MS.cluster_centers_
uni_labels = np.unique(labels)
n_clusters_ = len(uni_labels)
import matplotlib.pyplot as plt
from itertools import cycle
# 对算法聚类结果进行可视化
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
my_members = labels == k
cluster_center = cluster_centers[k]
plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=14)
plt.show()
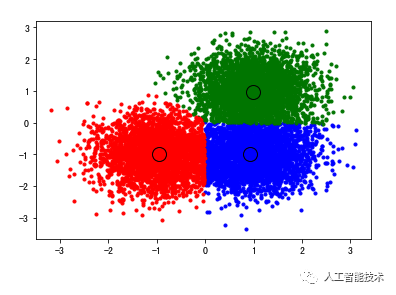
Mean Shift的实际应用
Mean Shift是聚类中常见的算法,以下展示了该算法在实际中的部分应用:
1. 简单聚类
mean shift用于聚类就有些类似于密度聚类,从单个样本点出发,找到其对应的概率密度局部极大点,并将其赋予对应的极大点,从而完成聚类的过程
2. 图像分割
图像分割的本质也是聚类,不过相对与简单聚类,图像分割又有其特殊性。mean shift通过对像素空间进行聚类,达到图像分割的目的。

3. 图像平滑
图像平滑和图像分割有异曲同工之妙,同样是对每一个像素点寻找其对应的概率密度极大点,主要区别在于:
a. 迭代过程不用深入,通常迭代一次即可;
b. 找到概率密度极大点后,直接用其颜色特征覆盖自身的颜色特征。

4. 轮廓提取
同样,轮廓提取与图像分割也是类似的,或者具体地说,轮廓提取可以基于图像分割进行。首先使用mean shift 算法对图像进行分割,然后取不同区域的边缘即可得到简单的轮廓

- EOF -
往期精彩回顾
适合初学者入门人工智能的路线及资料下载 (图文+视频)机器学习入门系列下载 机器学习及深度学习笔记等资料打印 《统计学习方法》的代码复现专辑 机器学习交流qq群955171419,加入微信群请扫码
