图像降维之MDS特征抽取方法
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
MDS,中文名叫“多维缩放”,是一种经典的降维方法,同时也是数据可视化的一种手段。最早起源于当我们仅能获得物体之间的相似性矩阵时,如何由此来重构它们的欧几里得坐标,如对一个国家的许多城市而言,假如我们不知道它们的经纬度信息,却知道所有城市两两之间的距离,就可以通过MDS方法重现它们的空间信息。MDS的基本思想很简单,要求原始空间中样本之间的距离在低维空间中得到保持。下面我们将对MDS的原理进行学习。
章节目录
准备知识
算法推导
算法步骤
实验
总结
实对称矩阵的特征分解性质
任意的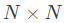 对称矩阵都有N个线性无关的特征向量,并且可以正交单位化。实对称矩阵A可被分解成:
对称矩阵都有N个线性无关的特征向量,并且可以正交单位化。实对称矩阵A可被分解成:
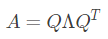
其中Q为正交矩阵,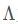 为实对角矩阵。
为实对角矩阵。
给定m个样本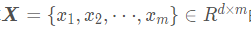 的距离矩阵
的距离矩阵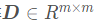 ,其中第i行第j列的元素
,其中第i行第j列的元素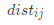 为样本
为样本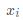 到
到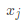 的距离。目标是获得低维表示
的距离。目标是获得低维表示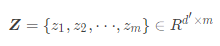 ,其中
,其中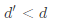 ,且保持任意两个样本在
,且保持任意两个样本在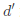 维空间的欧氏距离不变。
维空间的欧氏距离不变。
从已知的条件中,我们唯一能够得到降维后的样本与未降维前的样本之间的关系如下(1)式:
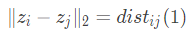
为了更清晰地观察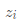 、
、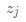 与
与 的关系,将(1)式左边平方,得(2)式:
的关系,将(1)式左边平方,得(2)式:
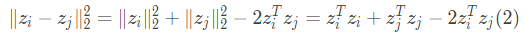
从(2)式可以看出,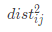 与
与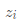 、
、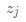 各自的模以及内积有关,为了能够统一表示这种关系,这里引入内积矩阵
各自的模以及内积有关,为了能够统一表示这种关系,这里引入内积矩阵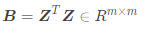 ,其中
,其中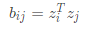 ,(2)式变换成(3)式:
,(2)式变换成(3)式:
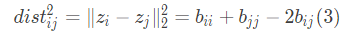
显然,我们接下来的目标是得到B中任一元素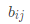 的解析解。在不影响结果正确性的前提下,为了方便后续计算,令降维后的样本Z被中心化,即
的解析解。在不影响结果正确性的前提下,为了方便后续计算,令降维后的样本Z被中心化,即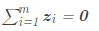 ,可以得到
,可以得到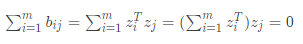 ,同理
,同理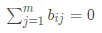 。则由(3)式可以得到式(4)(5)(6):
。则由(3)式可以得到式(4)(5)(6):
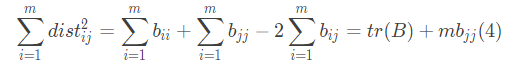
同理,
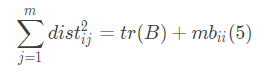
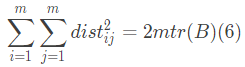
其中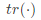 表示矩阵的迹(trace)。
表示矩阵的迹(trace)。
由(4)(5)(6)式得,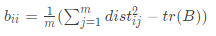 ,
,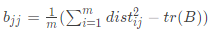 ,
,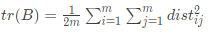 。
。
为了表述清晰,令
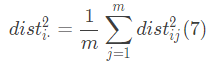
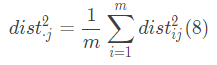
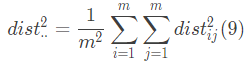
联合(3)和(4)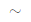 (9)式,得(10)式:
(9)式,得(10)式:
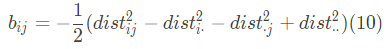
至此,已得到B和D的全部关系。接下来便是由B得到最终目标Z。
首先,我们可以判断出B是实对称矩阵,由实对称矩阵性质可知,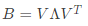 ,其中
,其中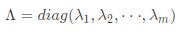 为特征值构成的对角矩阵,
为特征值构成的对角矩阵,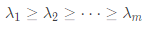 ,V是特征向量矩阵。
,V是特征向量矩阵。
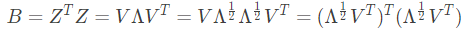
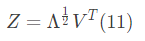
一般降维任务总是取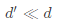 作为目标维度,所以取d'个最大特征值构成对角矩阵
作为目标维度,所以取d'个最大特征值构成对角矩阵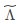 ,对应的特征向量矩阵为
,对应的特征向量矩阵为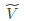 ,则
,则
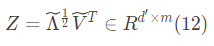
输入:距离矩阵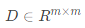 ,其元素
,其元素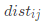 为样本
为样本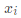 到
到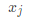 的距离;低维空间维数
的距离;低维空间维数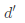 。
。
过程:
1: 根据(7)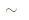 (9)式计算
(9)式计算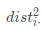 ,
, ,
,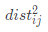 ;
;
2: 根据(10)式计算内积矩阵B;
3: 对B做特征值分解;
4: 取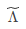 为
为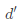 个最大特征值所构成的对角矩阵,
个最大特征值所构成的对角矩阵,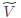 为相应的特征向量矩阵。
为相应的特征向量矩阵。
输出: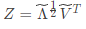
实验代码
"""
MDS : Multi-dimensional Scaling
Refercences :
[1]周志华.机器学习[M].清华大学出版社,2016:425.
[2]http://scikit-learn.sourceforge.net/dev/modules/generated/sklearn.manifold.MDS.html
Author : Ggmatch
Date : 2019/4/7
"""
from time import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter
from sklearn import manifold, datasets
# 制造样本
n_points = 1000
X, color = datasets.samples_generator.make_s_curve(n_points, random_state=0)
n_neighbors = 10
fig = plt.figure(figsize=(5, 5)) #画板
gs = fig.add_gridspec(1,2) #共2副子图
ax1 = fig.add_subplot(gs[0,0], projection='3d') #第一幅子图表示原始样本分布
ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
# MDS降维
n_components = 2
t0 = time() #计时开始
mds = manifold.MDS(n_components, max_iter=100, n_init=1) #建立MDS模型
Y = mds.fit_transform(X)
t1 = time() #计时结束
ax2 = fig.add_subplot(gs[0,1])
ax2.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral) #第2副子图表示降维后样本分布
ax2.set_title("MDS (%.2g sec)" % (t1 - t0))
ax2.xaxis.set_major_formatter(NullFormatter())
ax2.yaxis.set_major_formatter(NullFormatter())
plt.show()
实验效果
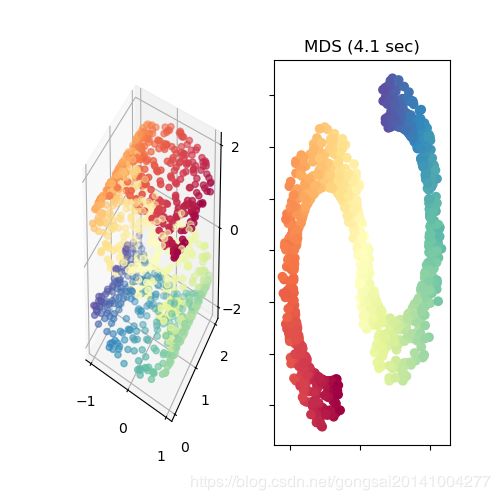
1)高维空间中对两个样本用欧式距离求直线距离,很多时候并不可取(如实验案例取得是流形空间),两点之间应该用“测地线”距离。改进算法为Isomap(Isomatric Mapping)。
2)MDS其实分为Metric MDS与Non-Metric MDS,本文讲述的是Metric MDS,通过样本之间的欧氏距离来近似代表相似度的思路,而Non-Metric MDS是通过点与点之间距离的单调映射来近似原有的距离。实际应用中,样本之间的距离越近,相似度越大,反之亦然。
References:
[1]https://baike.baidu.com/item/%E7%89%B9%E5%BE%81%E5%88%86%E8%A7%A3/12522621?fr=aladdin
[2]周志华.机器学习[M].清华大学出版社,2016:425.
[3]http://scikit-learn.sourceforge.net/dev/modules/generated/sklearn.manifold.MDS.html
[4]Cox, T.F., Cox, M.A.A. (2001). Multidimensional Scaling. Chapman and Hall.
[5]http://blog.sina.com.cn/s/blog_501162be0102v37l.html
交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~

