【特征工程】对比4大方法特征选择
特征选择能剔除和目标变量不相关(irrelevant)或冗余(redundant )的特征,以此来减少特征个数,最终达到提高模型精确度,减少运行时间的目的。
另一方面,筛选出真正相关的特征之后也能够简化模型,经常听到的这段话足以说明特征工程以及特征选择的重要性:
数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已
本文记录的是使用4种不同的方法来进行机器学习中特征的重要性排序,从而比较不同特征对目标变量的影响。4种方法是:
递归特征消除 线性模型 随机森林 相关系数
参考一篇博文:http://blog.datadive.net/selecting-good-features-part-iv-stability-selection-rfe-and-everything-side-by-side/
导入库
In [1]:
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
%matplotlib inline
from sklearn.feature_selection import RFE, f_regression
from sklearn.linear_model import (LinearRegression, Ridge, Lasso)
from sklearn.preprocessing import MinMaxScaler
from sklearn.ensemble import RandomForestRegressor
导入数据
In [2]:
house = pd.read_csv("kc_house_data.csv")
house
Out[2]:
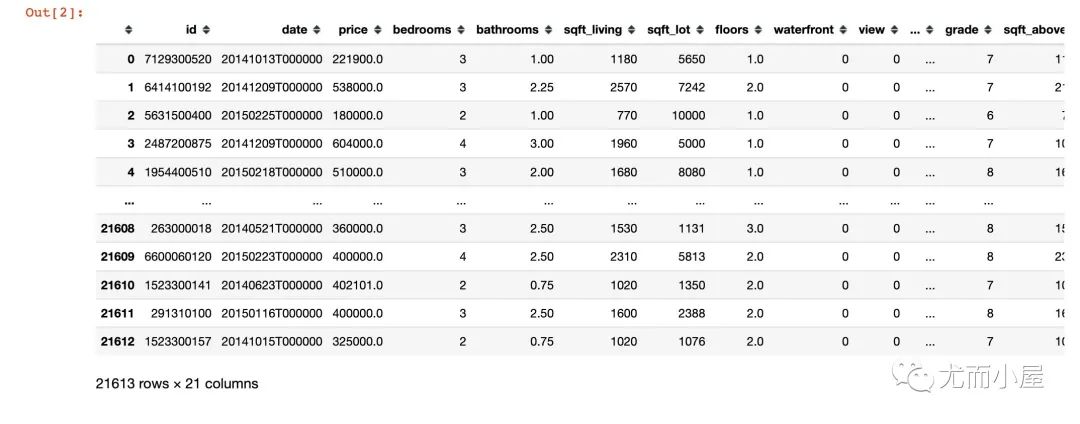
基本信息
In [3]:
# 数据shape
house.shape
Out[3]:
(21613, 21)
In [4]:
# 字段缺失值
house.isnull().sum()
Out[4]:
id 0
date 0
price 0
bedrooms 0
bathrooms 0
sqft_living 0
sqft_lot 0
floors 0
waterfront 0
view 0
condition 0
grade 0
sqft_above 0
sqft_basement 0
yr_built 0
yr_renovated 0
zipcode 0
lat 0
long 0
sqft_living15 0
sqft_lot15 0
dtype: int64
In [5]:
house.isnull().any() # 每个字段都没有缺失值
In [6]:
# 字段类型
house.dtypes
Out[6]:
id int64
date object
price float64
bedrooms int64
bathrooms float64
sqft_living int64
sqft_lot int64
floors float64
waterfront int64
view int64
condition int64
grade int64
sqft_above int64
sqft_basement int64
yr_built int64
yr_renovated int64
zipcode int64
lat float64
long float64
sqft_living15 int64
sqft_lot15 int64
dtype: object
删除无用字段
id和date两个字段直接删除掉:
In [7]:
house = house.drop(["id", "date"],axis=1)
Pairplot Visualisation
Pairplot中的plot就是成对、配对的意思,这种图形主要是显示变量两两之间的关系。
线性、非线性或者没有明显的相关性,都能观察到。下面的例子教你如何查看不同特征之间的关系:
In [8]:
fig = sns.pairplot(house[['sqft_lot','sqft_above','price','sqft_living','bedrooms']],
hue="bedrooms",
palette="tab20",
size=2
)
fig.set(xticklabels=[])
plt.show()
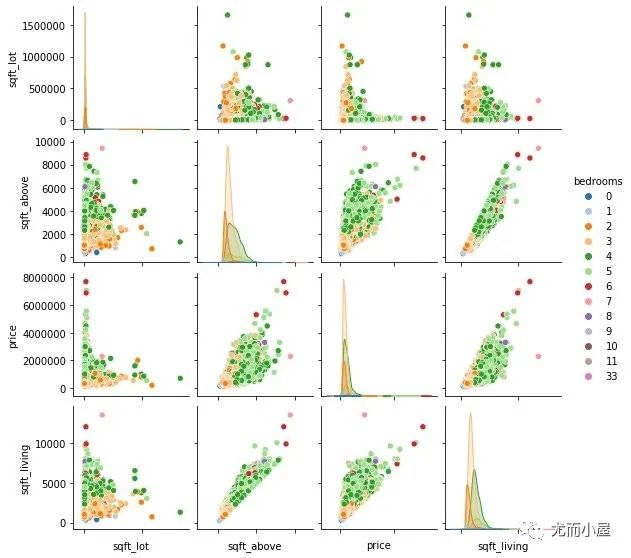
属性相关性热力图
属性之间的相关性只是针对数值型的字段,在这里我们先排除字符串类型的属性。
In [9]:
# # 方法1:寻找字符类型的属性
# str_list = []
# for name, value in house.iteritems():
# if type(value[1]) == str:
# str_list.append(name)
# str_list
In [10]:
# 方法2
# house.select_dtypes(include="object")
在这里我们直接取出非字符类型的属性数据:
In [11]:
house_num = house.select_dtypes(exclude="object")
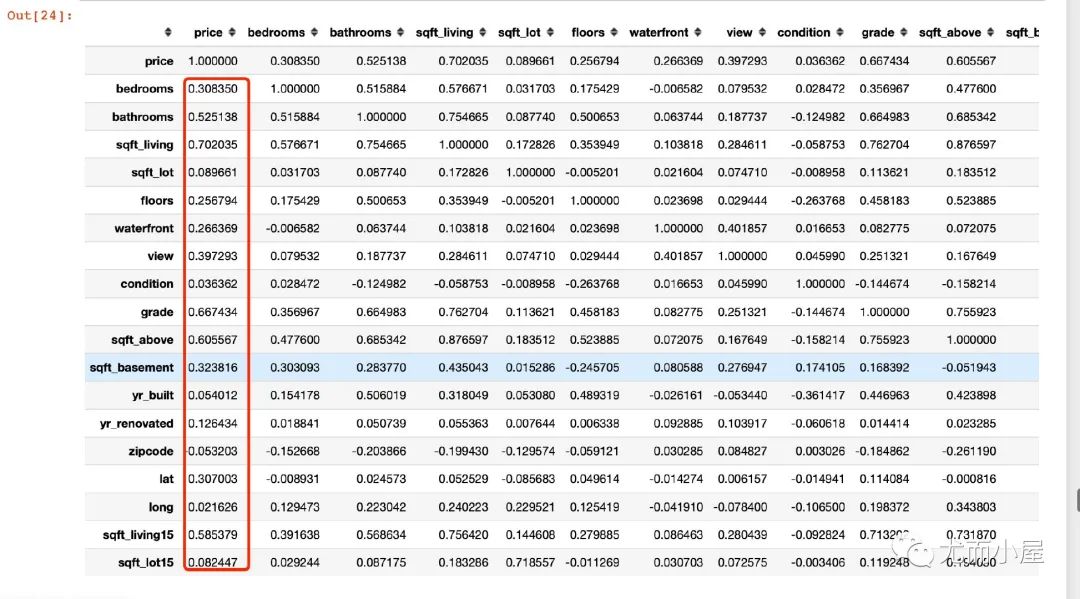
计算相关性和热力图:
corr = house_num.astype(float).corr()
# 绘制热力图
f, ax = plt.subplots(figsize=(16,12))
plt.title("Person Correlation of 19 Features")
sns.heatmap(corr, # 数据
linewidths=0.25, # 线宽
vmax=1.0, # 最大值
square=True, # 显示为方形
linecolor="k", # 线条颜色
annot=True # 注解;显示数据
)
plt.show()
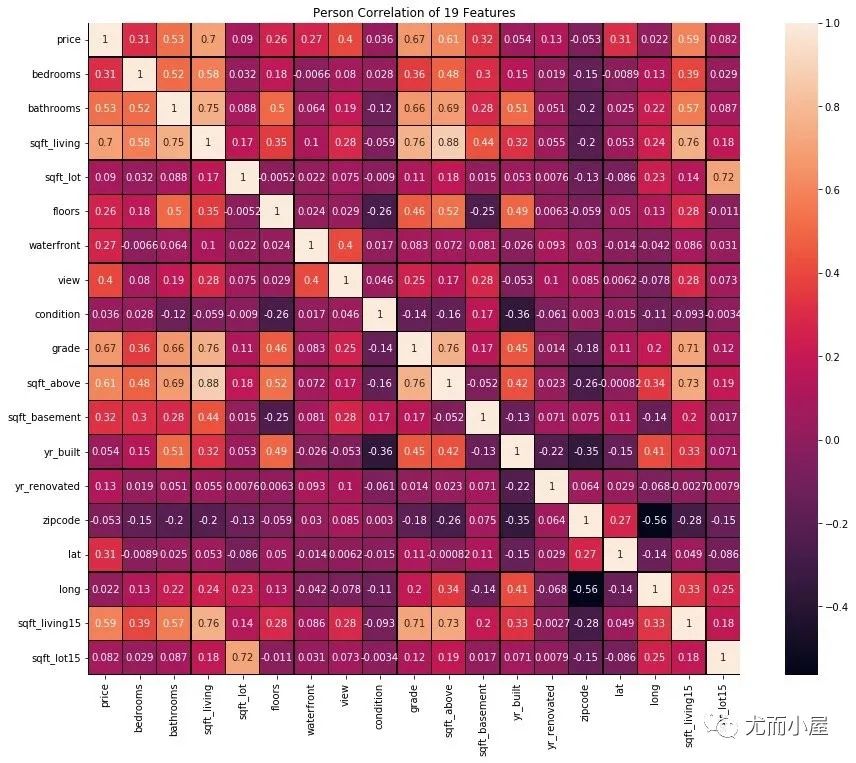
下面是用对其他3种方式进行特征的重要性进行探索,先实施数据的分割
数据分离
In [14]:
# 1、先提取目标变量
y = house.price.values # 目标变量
X = house.drop("price", axis=1) # 特征

计算特征的重要性
# 2、定义
ranks = {}
def ranking(ranks, names, order=1):
mm = MinMaxScaler() # 归一化实例
ranks = mm.fit_transform(order * np.array([ranks]).T).T[0]
ranks = map(lambda x: round(x,2), ranks)
return dict(zip(names, ranks))
基于RFE的特征排序
RFE:Recursive Feature Elimination,递归特征消除;
大致原理:通过反复地建立的线性回归或者SVM模型获得每个特征的coef_ 属性 或者 feature_importances_ 属性,并且对特征属性的重要性进行排序,从当前的特征集合中移除那些最不重要的特征,重复该过程。
Recursive Feature Elimination or RFE uses a model ( eg. linear Regression or SVM) to select either the best or worst-performing feature, and then excludes this feature
In [17]:
lr = LinearRegression(normalize=True)
lr.fit(X,y)
# 使用RFE的再次训练
rfe = RFE(lr, n_features_to_select=1,verbose=3)
rfe.fit(X,y)
ranks["RFE"] = ranking(list(map(float, rfe.ranking_)),
col_names,
order=-1
)
ranks # 特征和得分

上图显示的每个特征属性的得分;可以通过ranking_属性查看具体的排名:

基于线性模型的特征排序
下面尝试使用3种线性模型来进行特征排序
In [20]:
# 1、线性回归
lr = LinearRegression(normalize=True)
lr.fit(X,y)
ranks["LinReg"] = ranking(np.abs(lr.coef_), col_names)
# 2、岭回归
ridge = Ridge(alpha=7)
ridge.fit(X,y)
ranks["Ridge"] = ranking(np.abs(ridge.coef_), col_names)
# 3、Lasso回归
lasso = Lasso(alpha=0.05)
lasso.fit(X,y)
ranks["Lasso"] = ranking(np.abs(lasso.coef_), col_names)
ranks中新增的部分数据:

基于随机森林RandomForest的特征排序
随机森林主要是通过返回模型中的feature_importances属性来决定特征的重要性程度
In [22]:
rf = RandomForestRegressor(n_jobs=-1,
n_estimators=50,
verbose=3
)
rf.fit(X,y)
ranks["RF"] = ranking(rf.feature_importances_, col_names)
构造特征排序矩阵
将上面我们获取的每种方法的特征及其得分构造一个特征排序矩阵
生成特征矩阵
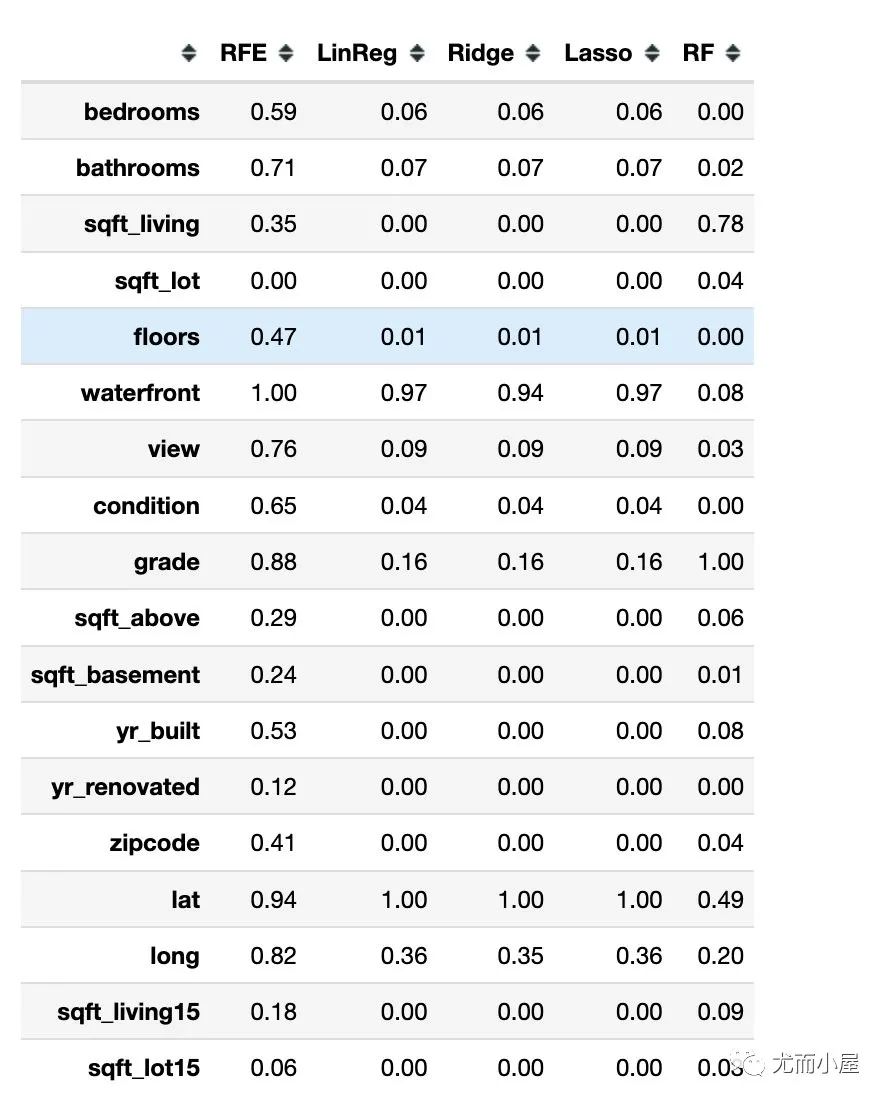
最后把特征和目标变量的相关系数添加进来一起对比:
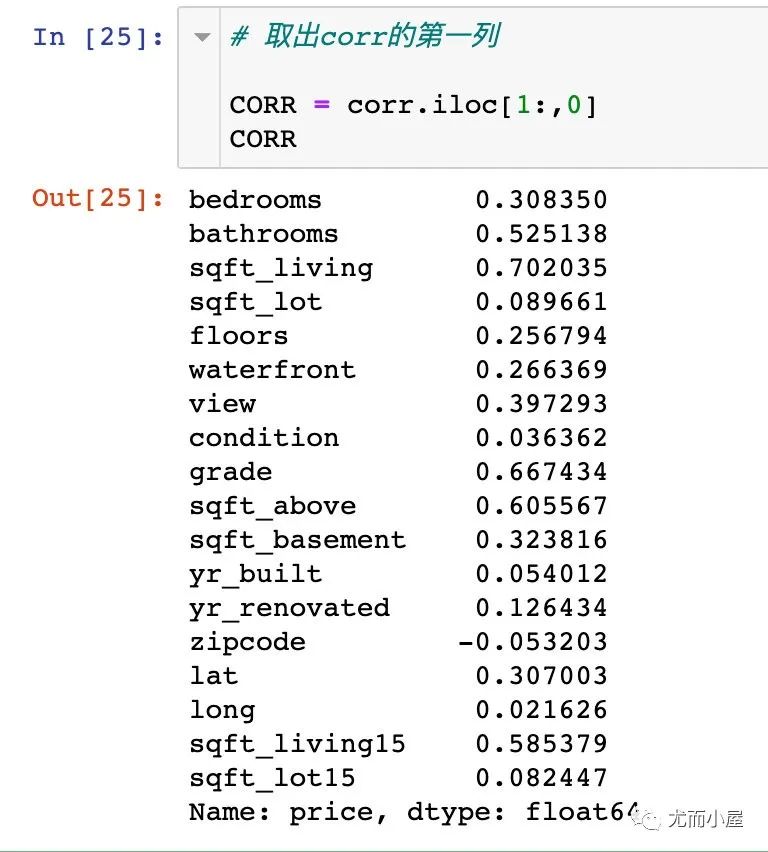
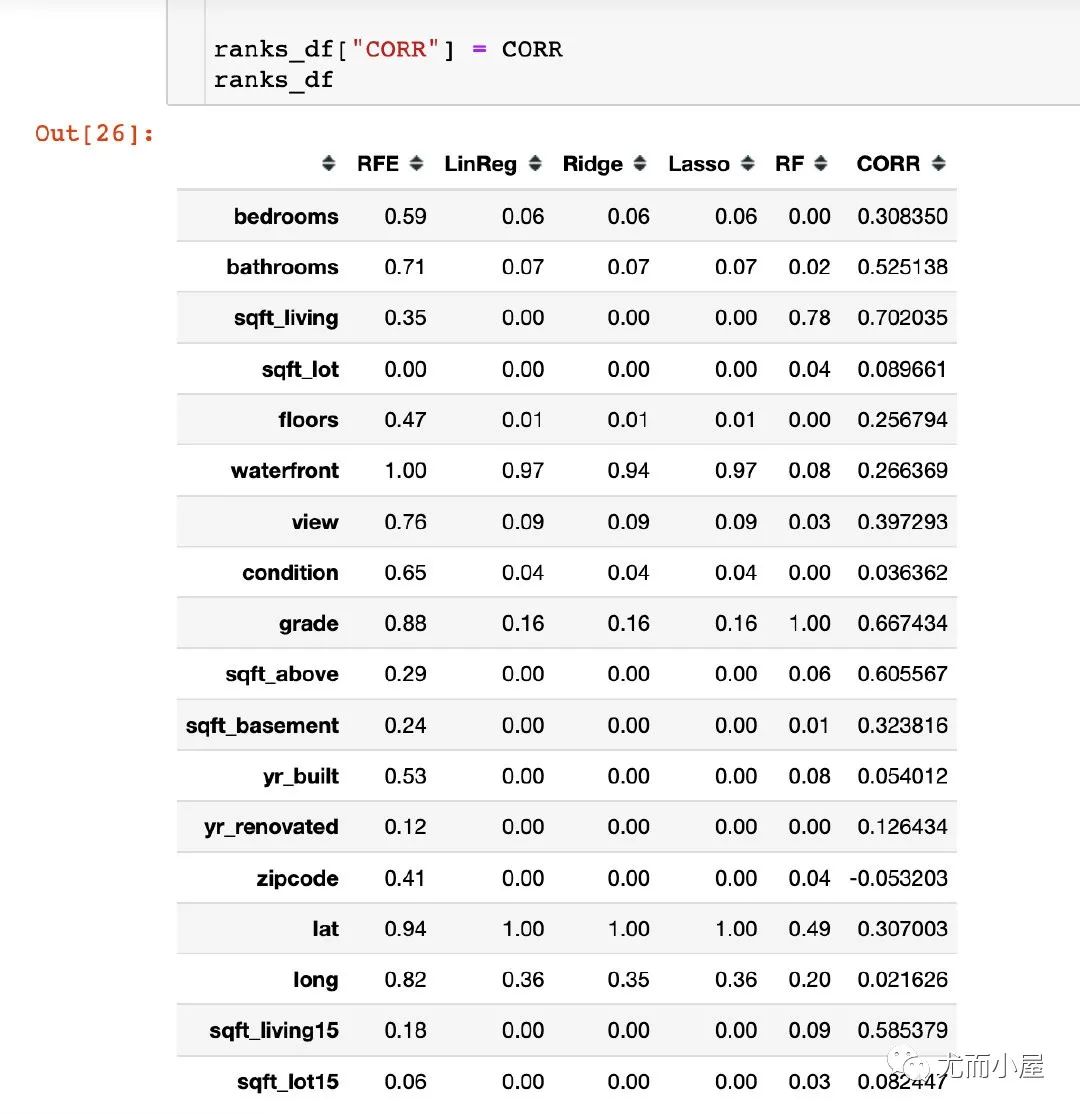
求出均值
求出所有方法下的均值:
In [27]:
ranks_df["Mean"] = ranks_df.mean(axis=1)
ranks_df
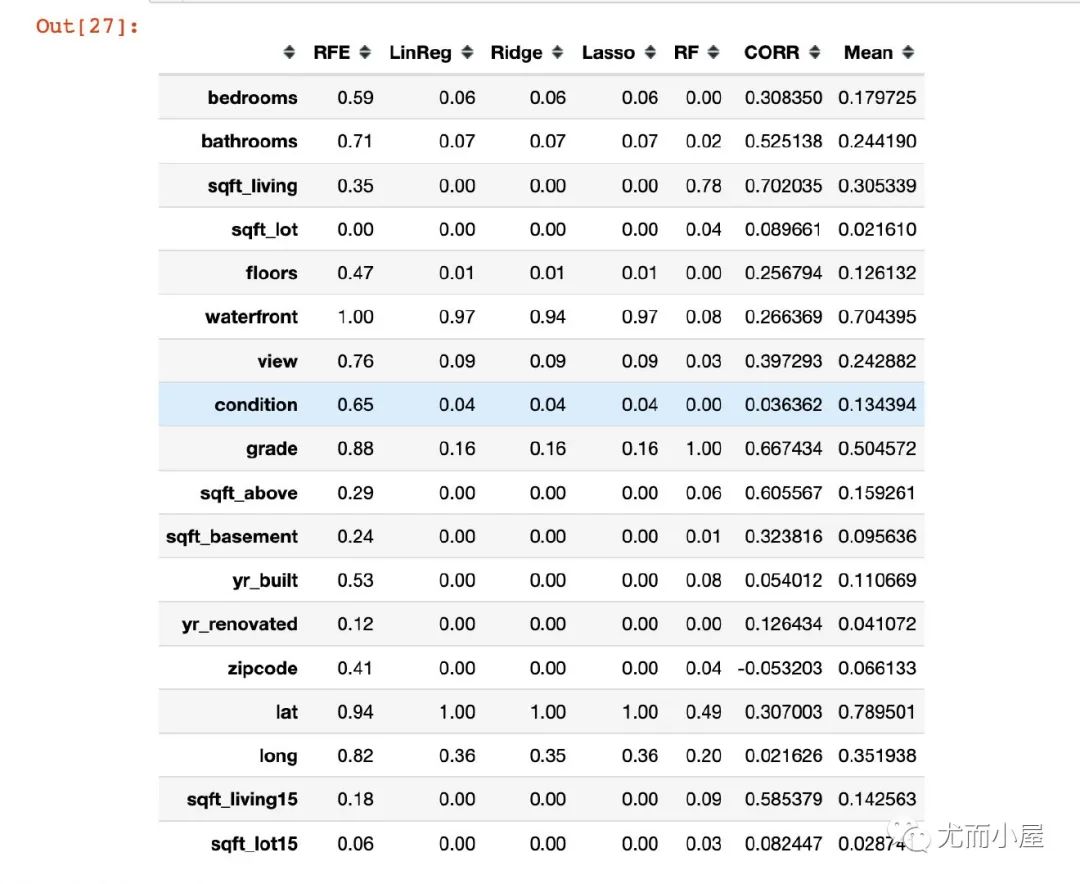
热力图显示
In [28]:
import seaborn as sns
cm = sns.light_palette("red", as_cmap=True)
s = ranks_df.style.background_gradient(cmap=cm)
s
Out[28]:
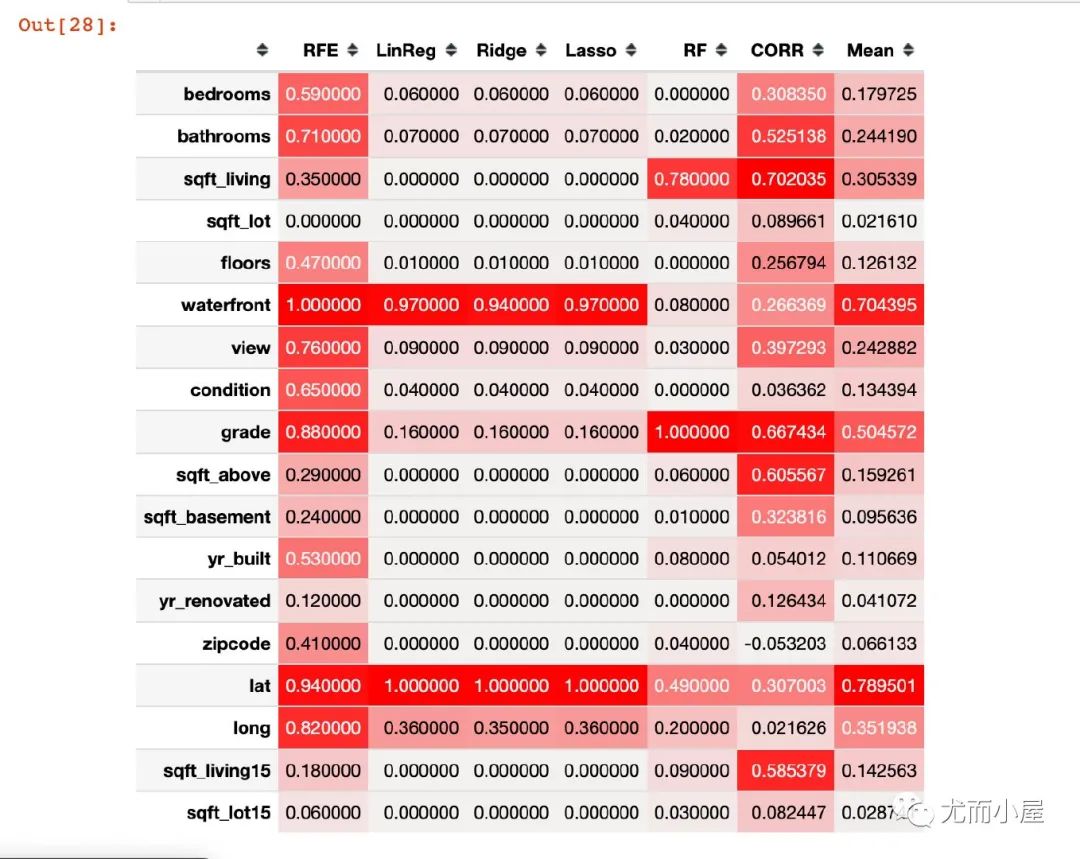
对比结果
RFE的重要性分数取值整体是偏高的;前两位是waterfront、lat 三种回归模型的得分比较接近,而且前两位和RFE是类型。可能原因是RFE选择的基模型是线性回归 随机森林模型最终得到3个特征的分数是比较高的:grade、sqft_living、lat 基于相关系数:得分排序的结果和随机森林接近
最后看看Mean的排名:
f = plt.figure(figsize=(12,8))
sns.barplot(y=df1.index.tolist(),
x=df1["Mean"].tolist()
)
plt.show()
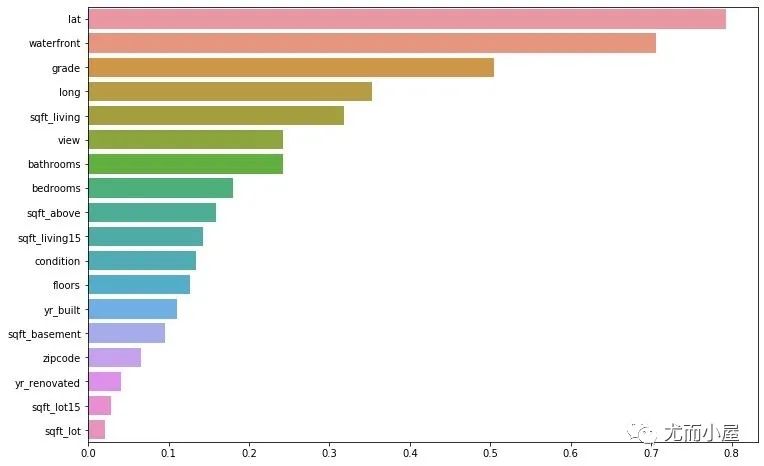
- END - 对比Excel系列图书累积销量达15w册,让你轻松掌握数据分析技能,可以点击下方链接进行了解选购:
