用 PCA 方法进行数据降维

在进行数据分析时，我们往往会遇到多维数据，多维数据在处理时由于维度较大计算起来非常麻烦，这时我们需要对数据进行降维。而在所有降维方法中，PCA是我们最常用的方法之一，其在使用时可以消除指标间的相互影响，同时也不用考虑数据的分布，而且降维效果非常明显，所以PCA可以在绝大多数情况下使用。而本文就是用python来解释一下如何用PCA方法进行降维。

首先对PCA进行一下简介。PCA全称是principal components analysis，即主成分分析。假设对某一事物的研究设计p个指标，分别用X1、X2、......、Xp表示，这p个指标构成的p维随机向量为X=(X1, X2, ..., Xp)’，设X的均值为μ，协方差矩阵为Σ。对X进行线性变换，可以形成新的综合变量，用Y表示，也就是说新的变量可以由原来的变量线性表示，即满足图1中的关系。

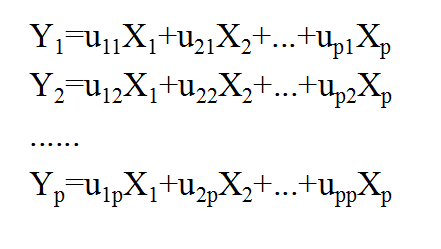
图1. PCA原理

import numpy as np 
import pandas as pd 
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

接下来读取相关数据集，这个数据集位于seaborn库当中。前8行数据如图2所示。

data = sns.load_dataset('iris')
data.head(8)

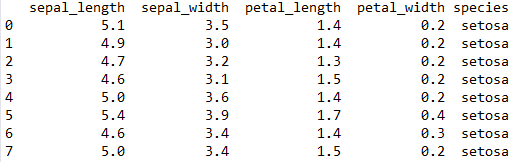
图2. 数据集样例

然后对数据做一个简单的处理，看一下各个维度之间的相关关系。所得结果如图3和图4所示。

values = data.iloc[:, :4] #读取前4列数据
correlation = values.corr() #列与列之间的相关系数
fig, ax = plt.subplots(figsize=(12, 10))
sns.heatmap(correlation, annot=True, annot_kws={'size':16}, cmap='Reds', square=True, ax=ax) #热力图
sns.pairplot(data, hue='species') #散点关系图

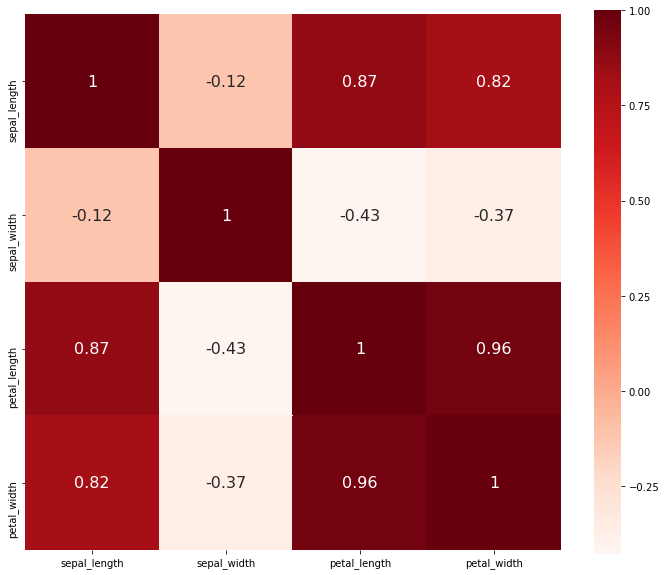
图3. 各维度之间的相关系数热力图

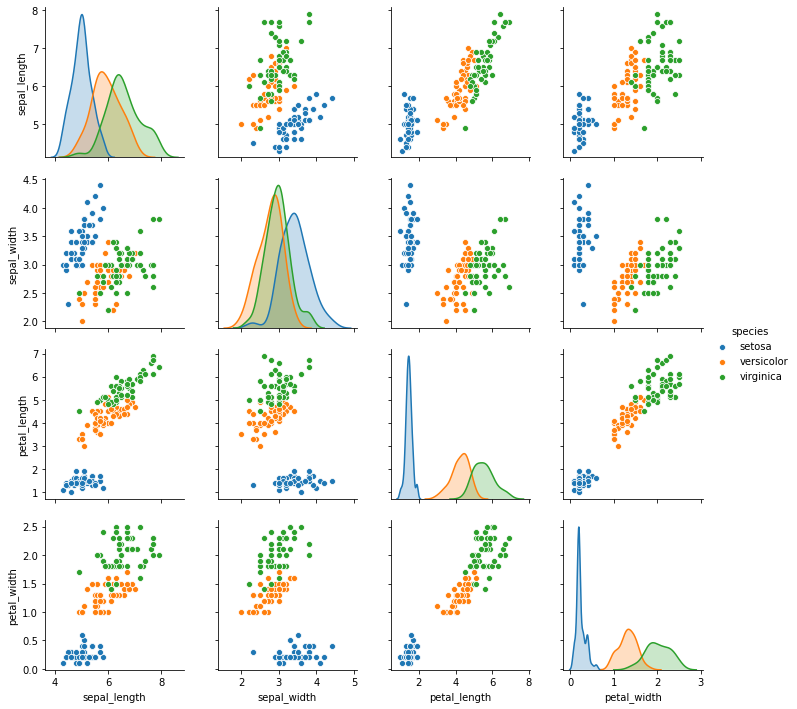
图4. 各维度之间的散点关系图

从图中可以大致看出，sepal_length和petal_length与petal_width都有较强的相关性，而petal_length和petal_width的相关性最强，达到0.96。下面我们来用PCA具体来分析一下该数据集，首先先看看该数据在选取4个主成分下的情况，这时候其主成分的数量和原数据的维度数相等。其结果如图5所示。

pca = PCA(n_components=4) #选取4个主成分
pc = pca.fit_transform(values) #对原数据进行pca处理
print("explained variance ratio: %s" % pca.explained_variance_ratio_) #输出各个主成分所占的比例
plt.plot(range(1, 5), np.cumsum(pca.explained_variance_ratio_)) #绘制主成分累积比例图
plt.scatter(range(1,5),np.cumsum(pca.explained_variance_ratio_))
plt.xlim(0, 5)
plt.ylim(0.9, 1.02)
plt.xlabel("number of components")
plt.ylabel("cumulative explained variance");

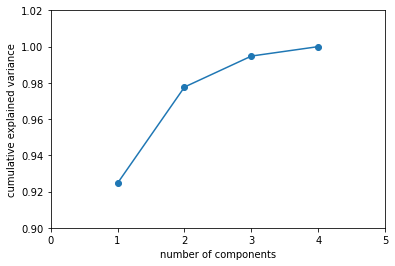
图5. 各主成分累加结果

我们可以看到pca.explained_variance_ratio_的结果是[0.92461872 0.05306648 0.01710261 0.00521218]，而图5中也显示前两个主成分之和就已经接近所有主成分的98%，所以在只考虑前两个主成分的情况下，我们就能够将数据的损失控制在很小的范围内。这里我们就只用前两个主成分来做分析。接下来我们就只用前两个主成分来分析原数据，将两个主成分的数据转换成dataframe格式，然后再加上一列原数据中species的数据，代码如下，结果如图6所示。

pca1 = PCA(n_components=2) #选取2个主成分
pc1 = pca1.fit_transform(values) 
pc1_df = pd.DataFrame(pc1, columns=['pc_1', 'pc_2'])
pc1_df['species'] = data['species'] #加上一列species
pc1_df.head(8)

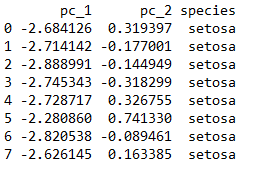
图6. 只有两个主成分的数据样例

接下来我们来看一下这两个主成分的组成。

print(pca1.components_)

结果如下。

[[ 0.36138659 -0.08452251  0.85667061  0.3582892 ]
 [ 0.65658877  0.73016143 -0.17337266 -0.07548102]]

用这个结果来验证一下前面的数据。按照图1中的原理来计算，pca1.components_第一行的数据和values第一行数据对应项相乘的和，应该等于pc1_df中pc_1列第一个数据-2.684126，即图6中第一行第一列数据。即有下列代码。

print(np.dot(pca1.components_[0], values.iloc[0]))

按照上式计算，结果是2.8182395066394683。很多人看到这里，认为是不是算错了，其实我们在计算方法上都没有错，只是在这里有一个隐含条件没有满足，就是sklearn在进行PCA计算时，数据要进行“中心化”，即每个数据减去这组数据的平均值，这样做主要是为了后续方便计算。所以我们要把上述代码改为下面这样。

print(np.dot(pca1.components_[0], values.iloc[0]-values.mean(axis=0)))

其得到的结果是-2.684125625969536，这就和前面的-2.684126对应起来了（这里排除小数点精度问题）。接下来就是用我们降维后的数据来作图。我们将原先的数据从4维降为2维，这正好方便绘制二维图，代码如下。结果如图7所示。

setosa = pc1_df[pc1_df['species']=='setosa'] #找出setosa对应的主成分数据
virginica = pc1_df[pc1_df['species']=='virginica']
versicolor = pc1_df[pc1_df['species']=='versicolor']
fig, ax = plt.subplots(figsize=(10, 8))
plt.scatter(setosa['pc_1'], setosa['pc_2'], alpha=0.7, color = 'red', label='Setosa') #绘制Setosa的散点图
plt.scatter(virginica['pc_1'], virginica['pc_2'], alpha=0.7, color = 'green', label='Virginica')
plt.scatter(versicolor['pc_1'], versicolor['pc_2'], alpha=0.7, color = 'blue',  label='Versicolor')
plt.legend(loc='best')
plt.xlabel('principal component 1')
plt.ylabel('principal component 2')

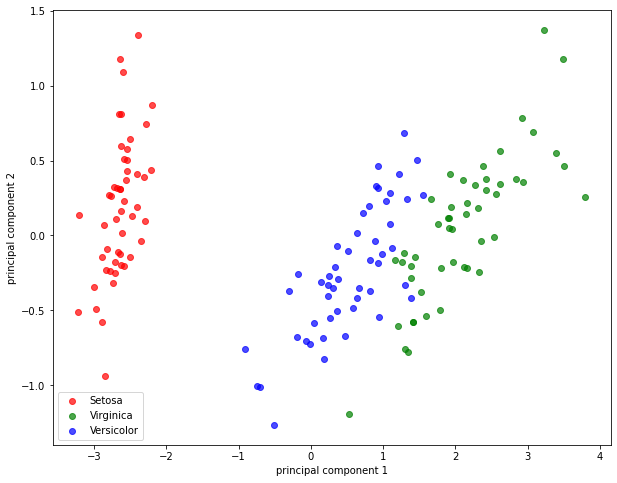
图7 . 降维后的散点图

主成分分析这种方法虽然简单易用，但其也有自身的缺点，比如对降维最终得到数目，不能很好地估计，同时PCA对于维度之间非线性的依赖关系不能得到很好的结果。此外本例中笔者没有对原数据进行标准化，因为标准化可能会损失一定信息，这个问题业界也争论了很长时间，到底是否对数据进行标准化需要根据实际情况来判断，因为本例中各维度之间的数据差异不大，所以笔者并未进行标准化。所以针对PCA的使用，大家还是要根据数据的要求来进行判断。

作者简介：Mort，数据分析爱好者，擅长数据可视化，比较关注机器学习领域，希望能和业内朋友多学习交流。

Python中文社区作为一个去中心化的全球技术社区，以成为全球20万Python中文开发者的精神部落为愿景，目前覆盖各大主流媒体和协作平台，与阿里、腾讯、百度、微软、亚马逊、开源中国、CSDN等业界知名公司和技术社区建立了广泛的联系，拥有来自十多个国家和地区数万名登记会员，会员来自以工信部、清华大学、北京大学、北京邮电大学、中国人民银行、中科院、中金、华为、BAT、谷歌、微软等为代表的政府机关、科研单位、金融机构以及海内外知名公司，全平台近20万开发者关注。