3D数学基础(二)| 向量
共 1701字，需浏览 4分钟
·
2021-12-29 21:14
前言3D数学基础：图形与游戏开发
这是白玉无冰记录3D数学第二篇章，向量！往期目录如下：
在写之前，白玉无冰一直在思考如何去讲述向量，思来想去，还是以实际问题例子出发，去讲这个神奇的向量！
本文不打算讲过多的定义和推导，更多地以例子出发去探讨。如果需要更深入地理解，可参考文末给出的参考书籍与资料。
开始基本定义
向量(vector)描述了方向和大小。向量也有自己的运算规则，向量的加减法与数乘的意义见下图。
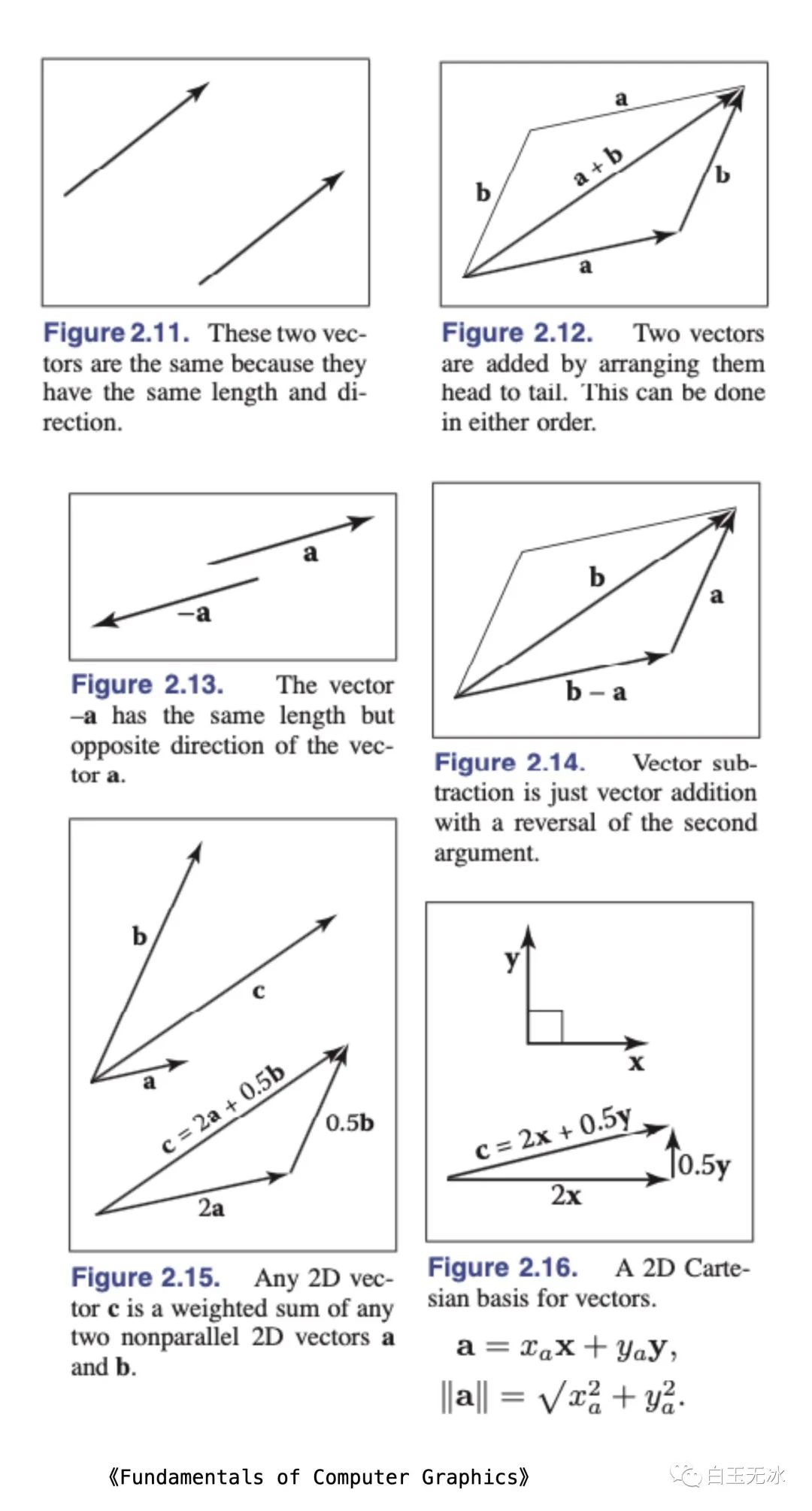向量加法与数乘除了向量间的加法，向量之间还存在着两种乘法：
- 点乘(Dot Product)
- 叉乘(Cross Product)
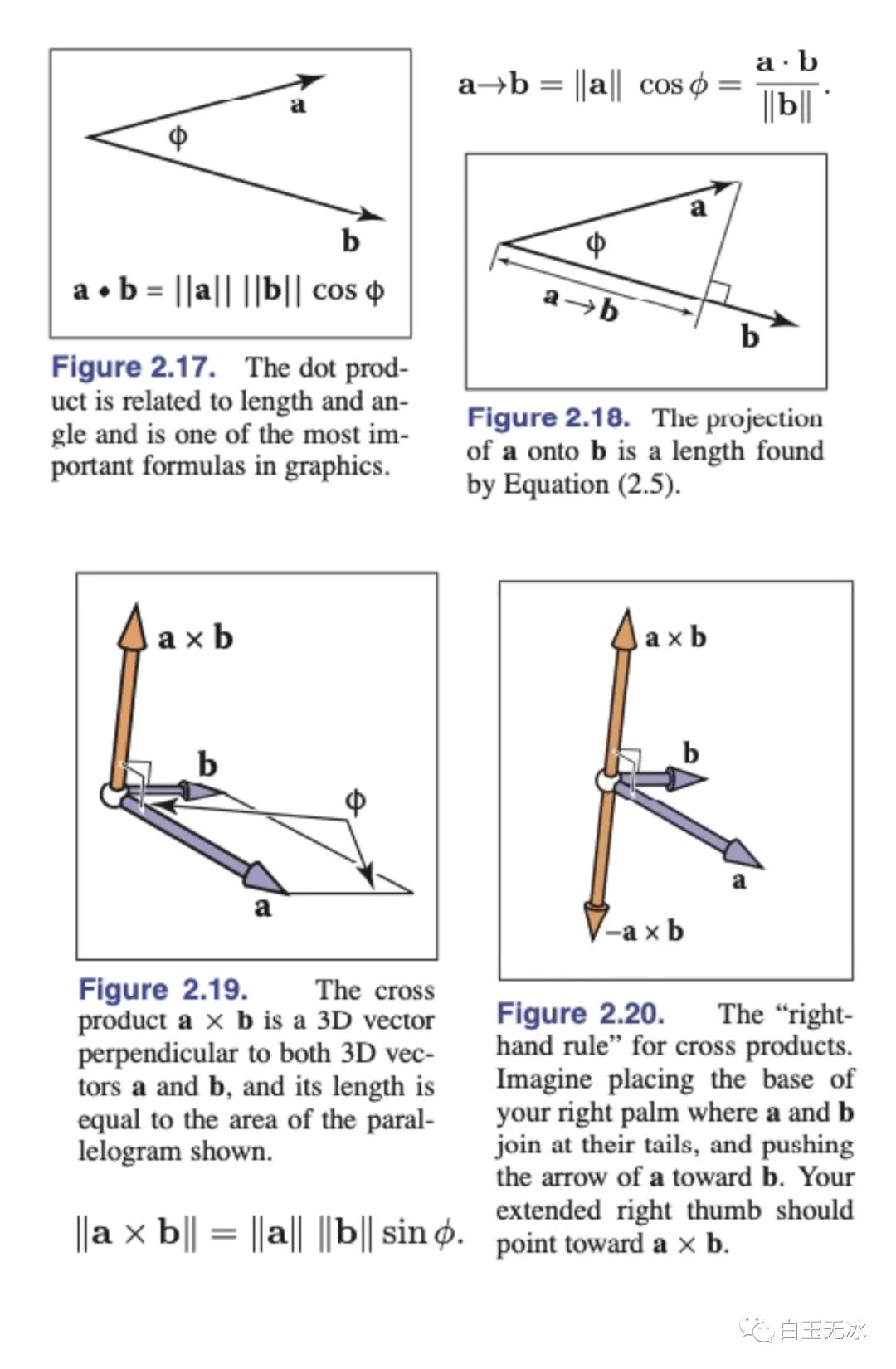向量点乘与叉乘向量反射
已知：
- 入射向量
- 单位法线量
- 入射角与反射角相同
求:
- 反射向量
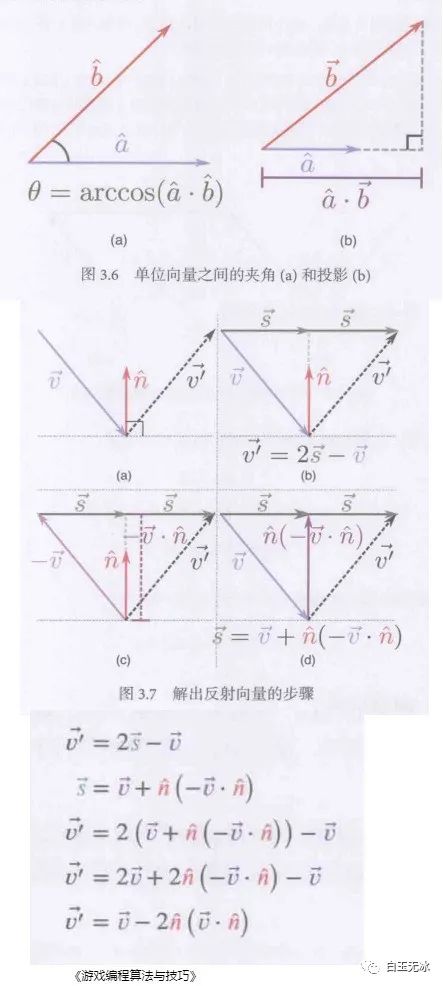向量反射在反复横跳的瞄准线这篇文章也用到了反射向量的计算。
反复横跳的瞄准线旋转2D角色
已知：
- 角色位置和朝向
- 目标位置
求:
- 角色往哪个方向旋转多少度可朝向目标位置
旋转2D角色概况来说，求角度用点乘，求旋转方向用叉乘。
旋转2D角色求解在 Cocos Creator 中的 Vec2 使用 signAngle 的逻辑也是如此。
// class Vec2
/**
* @en Get angle in radian between this and vector with direction.
* @zh 获取当前向量和指定向量之间的有符号角度。
* 有符号角度的取值范围为 (-180, 180]，当前向量可以通过逆时针旋转有符号角度与指定向量同向。
* @param other specified vector
* @return The signed angle between the current vector and the specified vector (in radians); if there is a zero vector in the current vector and the specified vector, 0 is returned.
*/
public signAngle (other: Vec2) {
const angle = this.angle(other);
return this.cross(other) < 0 ? -angle : angle;
}
判断多边形凹凸点
已知：
- 多边形的顶点坐标（逆时针，简易多边形）
求：
- 判断每个点的凹凸性
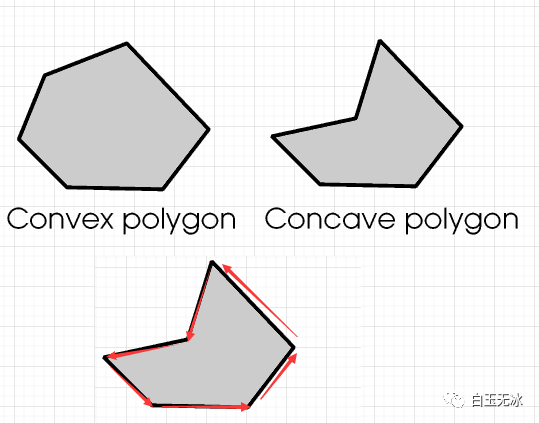凹凸多边形巧用向量叉乘即可求解。
在多边形裁剪图片中的切耳法用到了这个判断。
判断三角形内的点
已知：
- 三角形三个点
- 其中一个共面的点
求：
- 该点是否在三角形内
判断点是否在三角形内，可以通过叉乘计算点与线的位置关系判断出。
点是否在三角形内在 GAMES 103-02 中提到，也可用法向量判断。
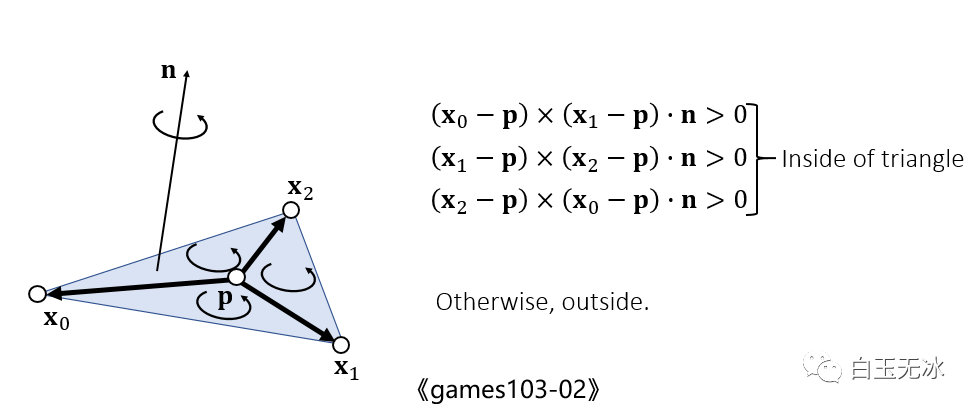点是否在三角形内前后左右
已知：
- 各个飞机的坐标和黑色飞机的朝向。
求：
- 其他飞机与黑色飞机前后左右的关系？
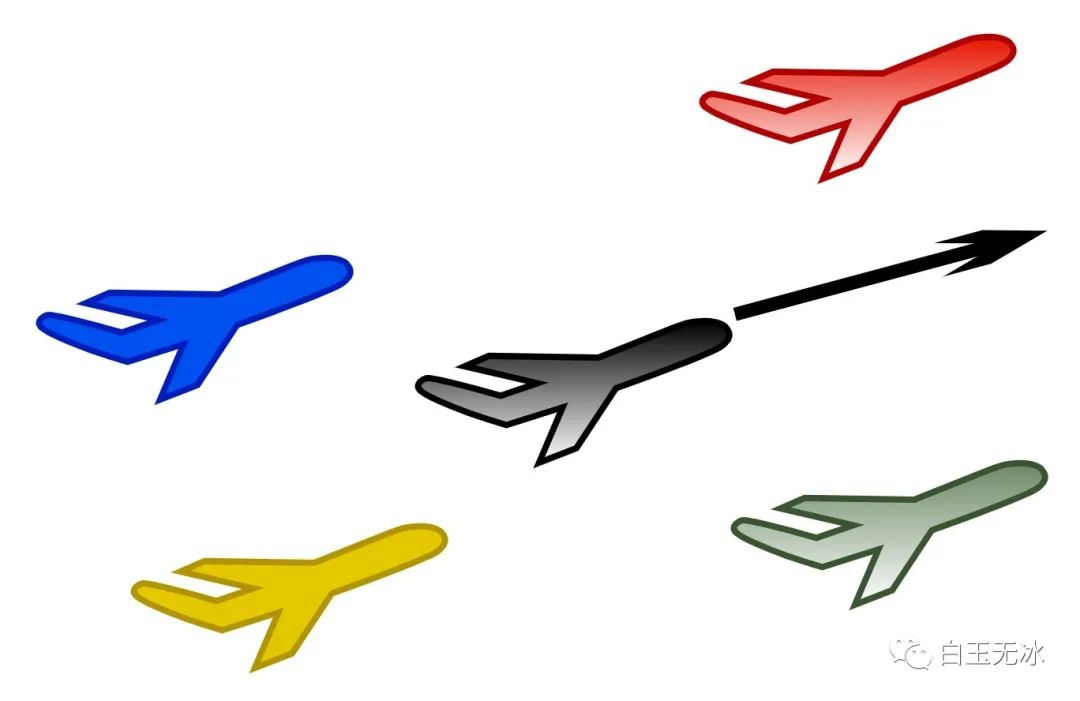前后左右解答：
- 点乘 -> 前后
- 叉乘 -> 左右
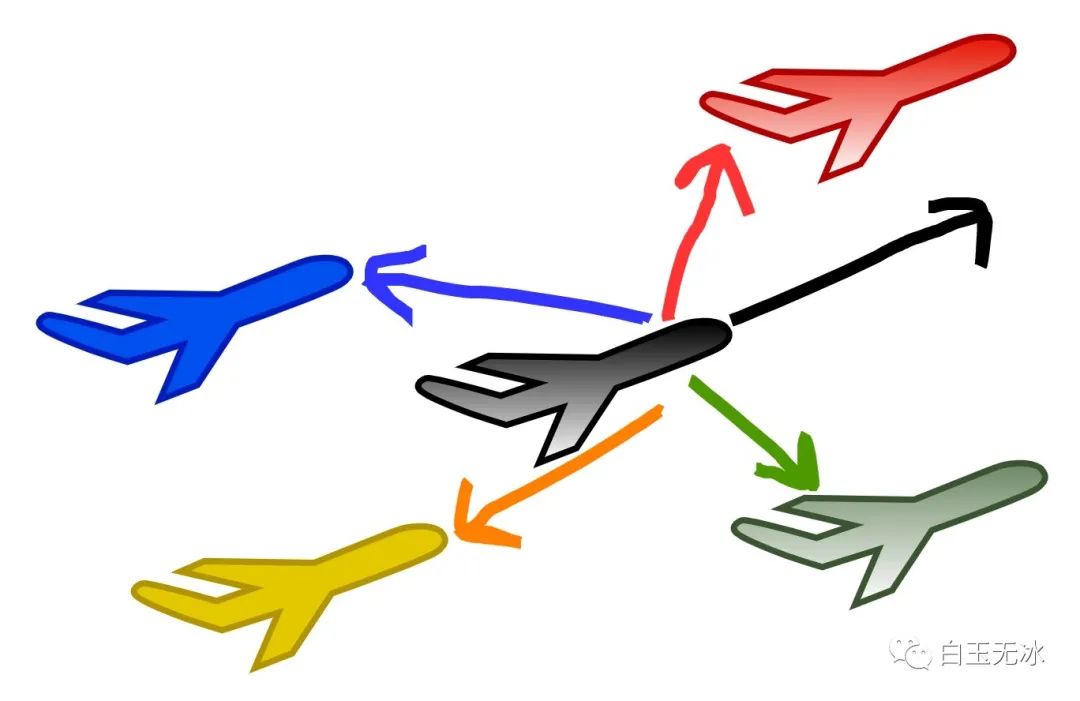前后左右折纸效果
在【折纸效果！(2D)】中也涉及一些向量计算，这里搬运过来，详细讲解可点击文章链接查看。
折纸效果分割多边形的点。向量间的点积正好可以帮助我们判断夹角问题。
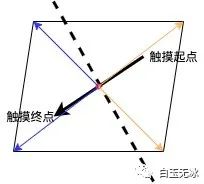分割求对称点同样可以运用向量计算。
- 求出该顶点与中点的向量
- 求出该点在触摸方向的单位向量的投影(点乘)，这正好是距离的一半
- 求出对称点坐标（距离乘方向向量+起始点坐标）
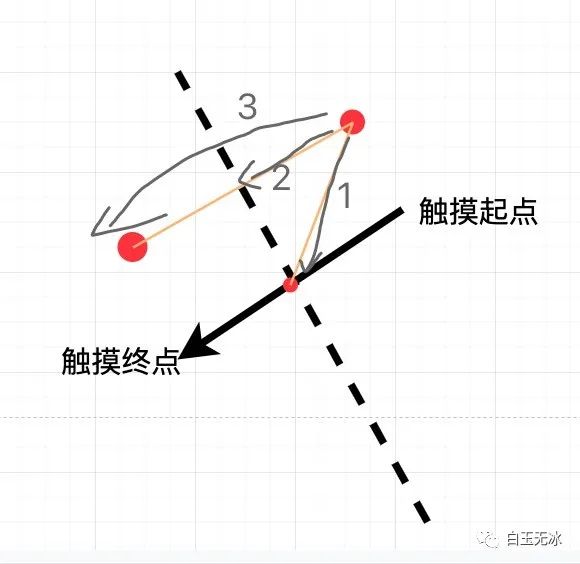求对称点在【3D折纸效果】同样也使用到向量相关的知识。
效果预览使用向量叉乘判断网格点在触摸轴的左边还是右边。
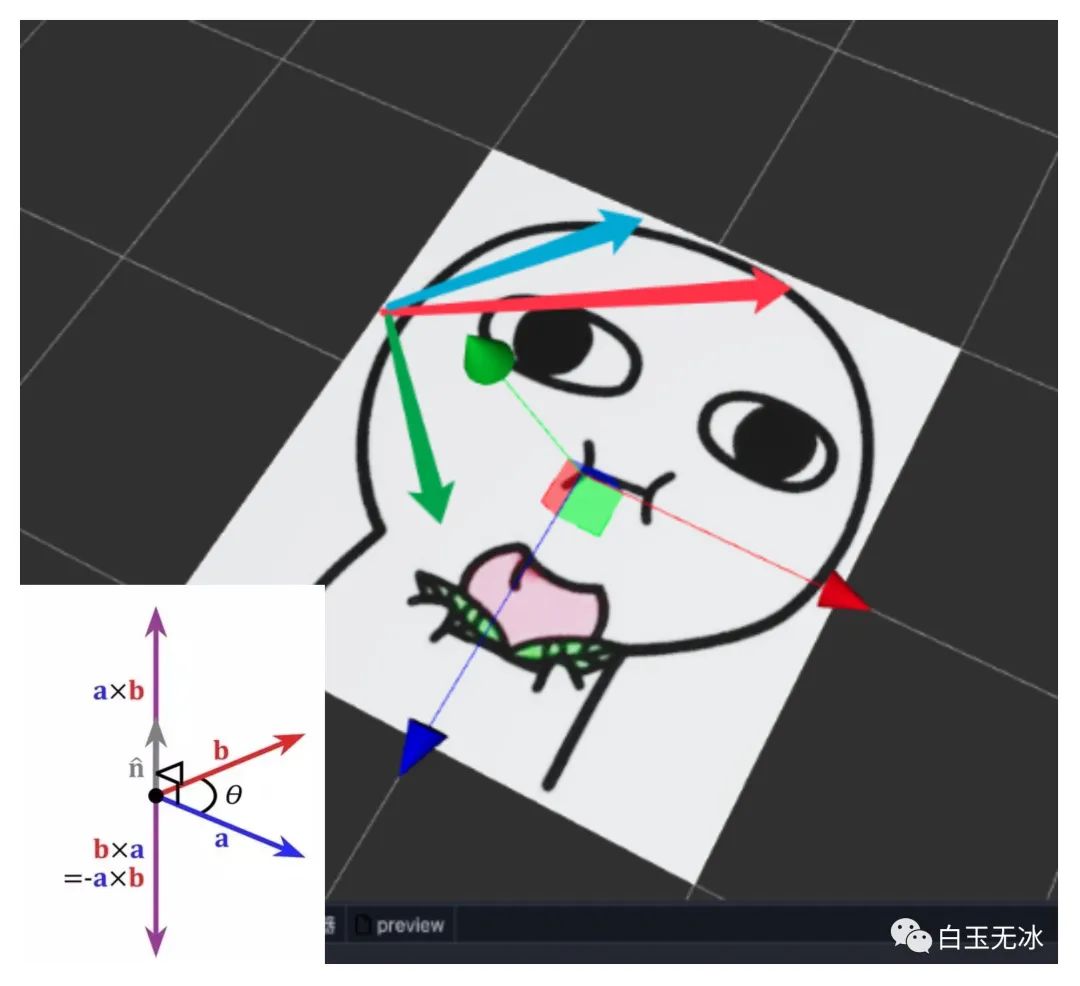向量叉乘矢量和平面
本段摘自《游戏编程精粹2》中的2.2章节。
已知：
- 起点 终点
- 平面单位法线向量 和面上的一个点
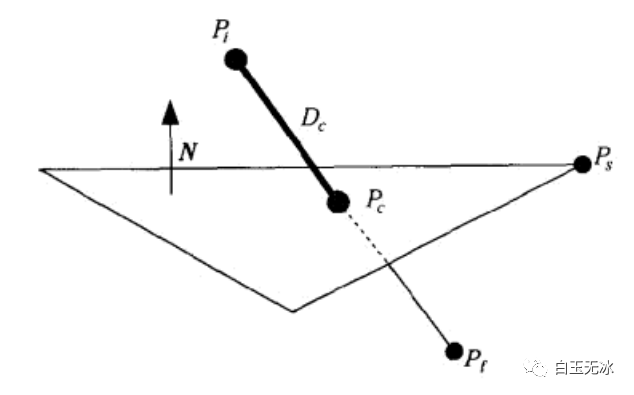矢量和平面求：相对于面的高度（点乘）
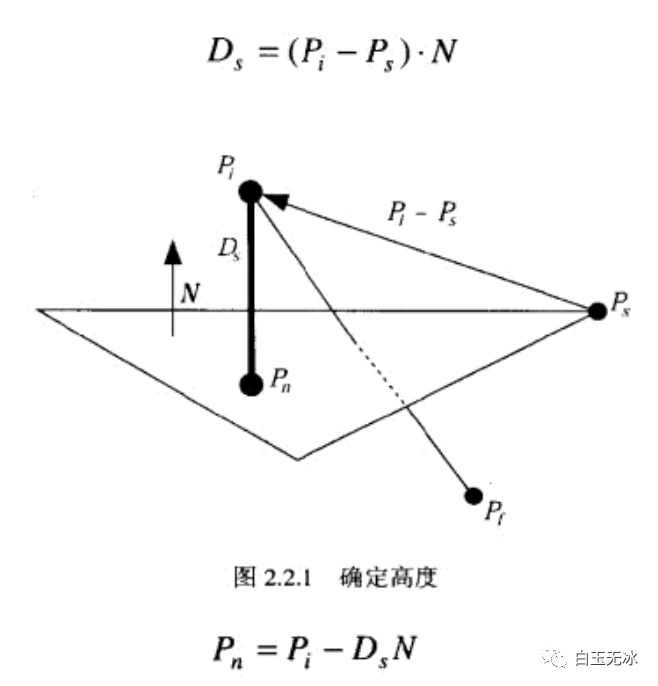相对于面的高度求：直接与平面相交点（投影到法向量，相似三角形）
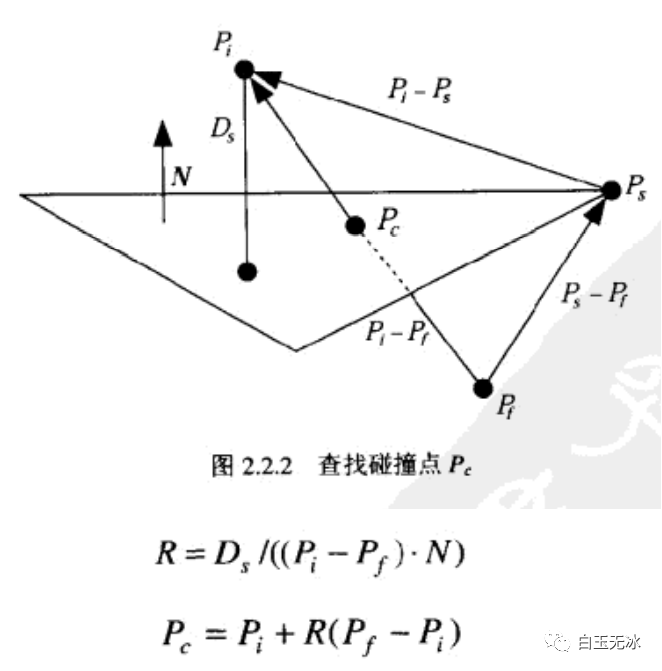直接与平面相交点求：到交点的距离（两种方法）
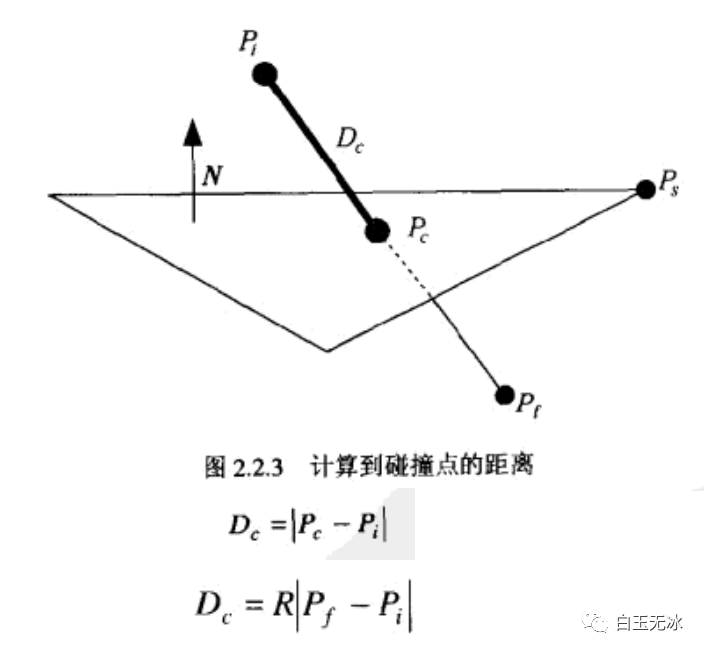到交点的距离计算反射点
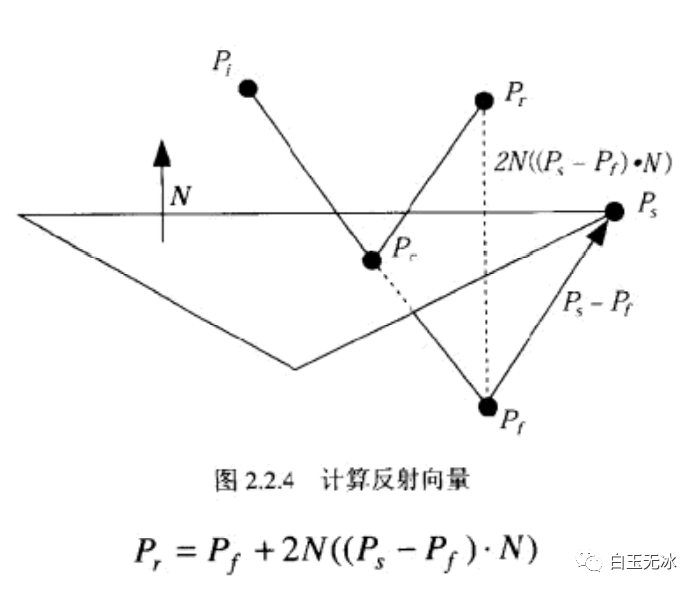计算反射点向量空间
本部分内容摘自《3D游戏与计算机图形学中的数学方法》1.4节，记录是为了更好的忘记。
向量空间向量的基
向量的基加上相互垂直条件，正交基
正交基再加上单位长度限制，正交规范基。
正交规范基自然数
讲到向量，这里再扯点其他和向量相关的。
自然数也可以分解成正交基向量表示。互质的自然数，正好与向量垂直对应。
自然数分解结束预期白玉无冰下一篇记录关于矩阵的笔记📒。
参考资料
- 《3D数学基础：图形与游戏开发》
- 《Fundamentals of Computer Graphics, Fourth Edition》
- 《游戏编程算法与技巧》
- http://games-cn.org/
- 《游戏编程精粹2》
- 《3D游戏与计算机图形学中的数学方法》
- 《数学女孩2》
更多精彩欢迎关注微信公众号
往期系列：