八十六、从拓扑排序探究有向图-技术圈

「@Author：Runsen」

关于排序，其实还有很多，比如常见的希尔排序，桶排序，计数排序和基数排序，由于要过渡到数据结构有向图，因此需要了解拓扑排序和邻接矩阵概念。

拓扑排序

拓扑排序本身并不是一个排序，排序是指一个数组数据，而且数据之间是没有任何联系的。

拓扑排序是从拓扑学引出来的概念，所谓的拓扑学(Topology)，是一门研究拓扑空间的学科，主要研究空间内，在连续变化（如拉伸或弯曲，但不包括撕开或粘合）下维持不变的性质。其实我也是一个半懂又不是很懂得状态。

下面先来看一个生活中的拓扑排序的例子，例子来源王争的算法专栏。

我们在穿衣服的时候都有一定的顺序，我们可以把这种顺序想成，衣服与衣服之间有一定的依赖关系。比如说，你必须先穿袜子才能穿鞋，先穿内裤才能穿秋裤。

假设我们现在有八件衣服要穿，它们之间的两两依赖关系我们已经很清楚了，那如何安排一个穿衣序列，能够满足所有的两两之间的依赖关系？

拓扑排序的原理非常简单，下面是一个牛客关于拓扑排序的选择题，好像是2017滴滴校招的笔试题，其实就是送分题。

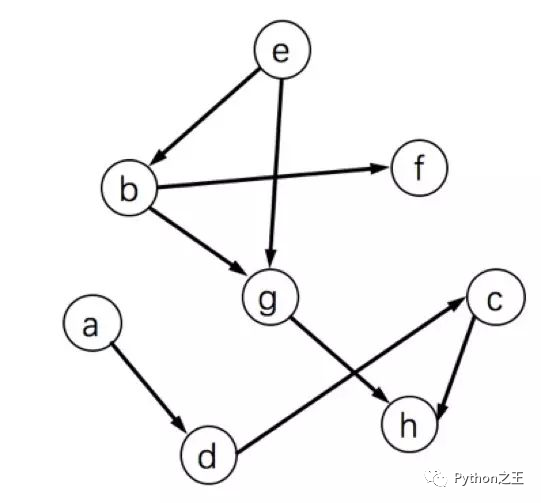
下面哪个序列不是上图的一个拓扑排序？

A. ebfgadch
B. adchebfg
C. aebdgfch
D. aedbfgch

答案是B，因为H不可能出现在中间，它是拓扑序的末尾，最多只能出现F前面。拓扑序定义如下：对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。

图

图是一个比树还有复杂的数据结构。

树中的元素我们称为节点，图中的元素我们就叫做顶点（vertex）。图中的一个顶点可以与任意其他顶点建立连接关系。我们把这种建立的关系叫做边（edge）。

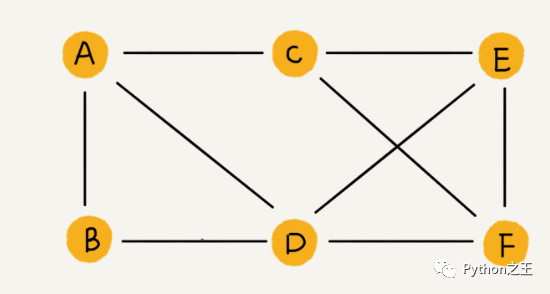
争哥把图比作成微信的好友关系，其实非常的形象。比如，上面图中的顶点都代表一个微信的用户。

整个微信的好友关系就可以用一张图来表示。其中，每个用户有多少个好友，对应到图中，就叫做顶点的度（degree），就是跟顶点相连接的边的条数。

至于有向图，争哥比喻成微博的社交关系，微博只允许单向关注，也就是说，用户 A 关注了用户 B，但用户 B 可以不关注用户 A。对于不玩微博的我，关于微博这种单向关注现在才知道。

如果用户 A 关注了用户 B，我们就在图中画一条从 A 到 B 的带箭头的边，来表示边的方向。如果用户 A 和用户 B 互相关注了，那我们就画一条从 A 指向 B 的边，再画一条从 B 指向 A 的边。我们把这种边有方向的图叫做“有向图”。

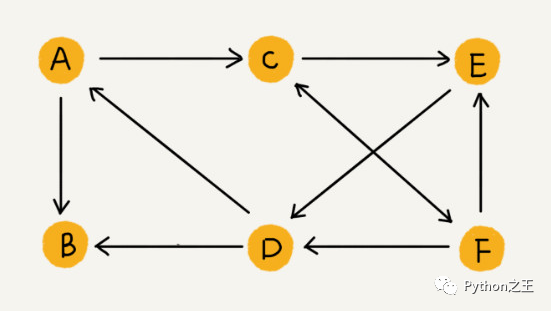
在有向图中，把度分为入度（In-degree）和出度（Out-degree）。对应到微博的例子，入度就表示有多少粉丝，出度就表示关注了多少人。

在带权图中，每条边都有一个权重（weight），我们可以通过这个权重来表示 QQ 好友间的亲密度。

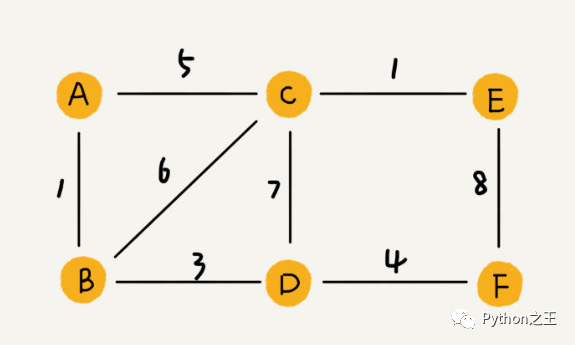
在图中，有一个非常重要的概念，叫「邻接矩阵」。

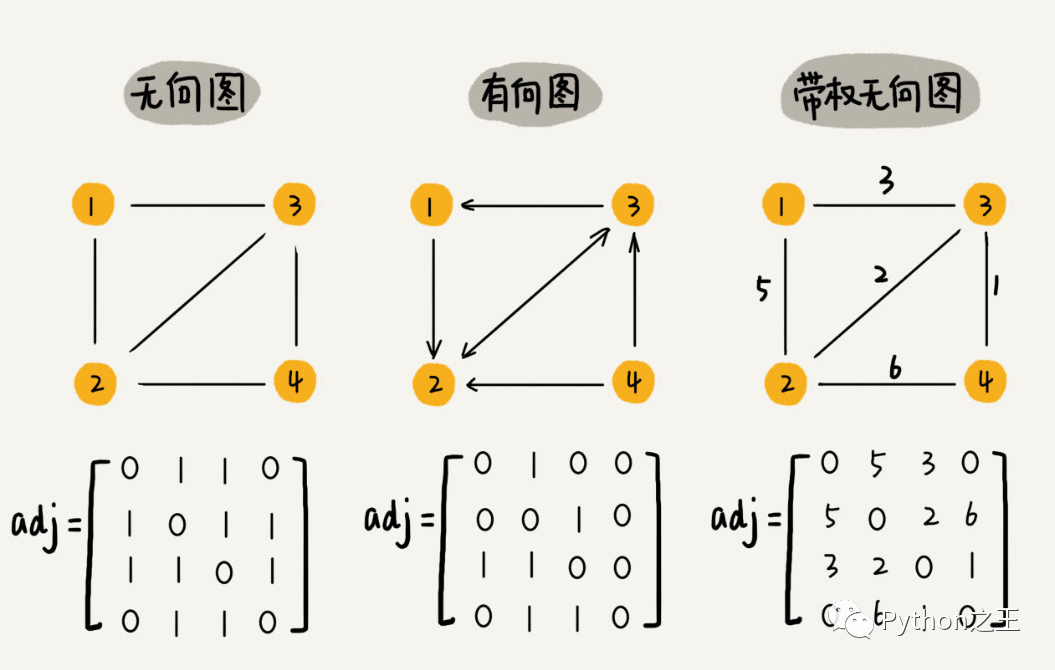
邻接矩阵的底层依赖一个二维数组。对于无向图来说，如果顶点 i 与顶点 j 之间有边，我们就将 A[i][j]和 A[j][i]标记为 1；对于有向图来说，如果顶点 i 到顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，那我们就将 A[i][j]标记为 1。同理，如果有一条箭头从顶点 j 指向顶点i 的边，我们就将 A[j][i]标记为 1。对于带权图，数组中就存储相应的权重。

有向无环图(Direct Acyclic Graph或DAG)是近些年来区块链项目的技术热点之一。搞Go方面的区块链，一上来就是有向无环图。

其实有向无环图也好理解的，“有向”指的是有方向，准确的说应该是同一个方向，“无环”则指够不成闭环，像上面例子的图。很多时候有向图，多指的是有向无环图。

「备注：上面文字和图片均来源王争算法专栏」

课程表

对于拓扑排序，在Leetcode比较有印象的是Leetcode第207 课程表

你这个学期必须选修 numCourse 门课程，记为 0 到 numCourse-1 。

在选修某些课程之前需要一些先修课程。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们：[0,1]

给定课程总量以及它们的先决条件，请你判断是否可能完成所有课程的学习？

示例 1:

输入: 2, [[1,0]] 
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

示例 2:

输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

这道题剥去包装的外衣后，其实是「有向图检测是否有环问题」，有环则代表修完全部课程不能实现。

对于判断拓扑排序是否有环，，其实是一种搜索算法的实现，因此我们很容易想到深度优先搜索和广度优先搜索。

广度优先搜索

首先说一下，BFS广度优先搜索的算法过程。

广度优先搜索可以以一种向四周发散的方式找到出口，即不是深度优先的。那么当我们走到一个点时就给该点打上标记，然后如果后面又走到了这个点，那么我们便发现这个迷宫存在着一条路径永远也走不出去，这样就可以看作是找到了一个有向环。

拓扑排序中最前面的节点，一定不会有任何入边，也就是它没有任何的先修课程要求。如果进入了队列中，那么就代表着这门课可以开始学习了。然后不断地将没有入边的节点加入队列中，直到队列中包含所有的节点（得到了一种拓扑排序）或者重新出现了之前入边的节点（图中包含环）。

算法流程：

统计课程安排图中每个节点的入度，生成入度表indegrees和邻接矩阵adjacency，入度表indegrees默认全是零的数组，而邻接矩阵adjacency是一个二维数组，也可以把邻接矩阵adjacency叫做课程安排图。
遍历传入的拓扑排序的必备条件，在这里是传入的prerequisites，学习当前课程，入度表对应的值需要置换成1，学习完之前课程就可以学习矩阵就要添加下一个要学习的课程。
借助一个队列 queue，将所有入度为0的节点入队。一开始如果queue为空，绝对存在环，直接判断numCourses == 0。
当 queue 非空时，依次将队首节点出队，在课程安排图中删除此节点 pre：

但并不是真正从邻接表中删除此节点 pre，而是将此节点对应所有邻接节点 cur 的入度 -1，即 indegrees[cur] -= 1。
当入度 -1后邻接节点 cur 的入度为 0，说明 cur 所有的前驱节点已经被 “删除”，此时将 cur 入队。

在每次 pre 出队时，执行 numCourses--；

若整个课程安排图是有向无环图（即可以安排），则所有节点一定都入队并出队过，即完成拓扑排序。换个角度说，若课程安排图中存在环，一定有节点的入度始终不为 0。
因此，拓扑排序出队次数等于课程个数，返回 numCourses == 0 判断课程是否可以成功安排。

具体广度优先搜索判断拓扑排序是否有环，具体的代码如下所示。

'''
@Author：Runsen
@WeChat：RunsenLiu 
@微信公众号：Python之王
@CSDN：https://blog.csdn.net/weixin_44510615
@Github：https://github.com/MaoliRUNsen
@Date：2020/12/27
'''
class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        # 记录要学习 index 表示的课程前得学习多少其他课程
        indegrees  = [0 for _ in range(numCourses)]
        # 邻接矩阵：记录学完 index 表示的课程后可学习的课程的集合
        adjacency = [[] for _ in range(numCourses)]

        for cur, pre in prerequisites:
            # 表示学习 cur 课程前得学习 indegrees [cur] 个课程
            indegrees[cur] += 1
            # 学习完 pre 课程就可以学习 adjacency[pre] 集合中的课程了
            adjacency[pre].append(cur)

        queue = []

        for course in range(numCourses):
            if indegrees [course] == 0: # 学习 course 课程不需要先学习其他课程
                queue.append(course)

        while queue:
            course = queue.pop(0)
            # 学习完了一个课程
            numCourses -= 1 
            for next_course in adjacency[course]:
                # next_course 的前置课程数量减少一个，因为 course 学完了
                indegrees [next_course] -= 1 
                if indegrees [next_course] == 0: # 表示学习 next_course 不需要先学习其他课程了
                    queue.append(next_course)
        return numCourses == 0

深度优先遍历

对于深度优先遍历DFS，个人觉得不好想。需要借助一个标志列表 flags，用于判断每个节点 i （课程）的状态：

未被 DFS 访问：i == 0；
已被其他节点启动的 DFS 访问：i == -1；
已被当前节点启动的 DFS 访问：i == 1。

深度优先遍历思路：「对numCourses个节点依次执行DFS，判断每个节点起步DFS是否存在环，若存在环直接返回 False。」

DFS流程的终止条件：

当 flag[i] == -1，说明当前访问节点已被其他节点启动的DFS访问，无需再重复搜索，直接返回 True。
当 flag[i] == 1，说明在本轮DFS搜索中节点 i 被第 2次访问，即课程安排图有环，直接返回False。

下面将当前访问节点 i 对应 flag[i] 置 1，即标记其被本轮 DFS 访问过；递归访问当前节点 i 的所有邻接节点 j，当发现环直接返回 False；

当前节点所有邻接节点已被遍历，并没有发现环，则将当前节点 flag 置为 -1并返回 True。

若整个图 DFS 结束并未发现环，返回 True。

DFS的操作步骤如下（递归方式）：1，初始化每个节点，令其访问标志为0 2，对初识节点调用DFS访问，只要p不空即（即边表不空)，如该节点没被访问过就递归调用DFS来访问，访问过以后标志记为1，否则p=p->next找下一个相邻节点 3 循环遍历，对每个节点执行相同的操作，直到全部访问完。

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        def dfs(i, adjacency, flags):
            if flags[i] == -1: return True
            if flags[i] == 1: return False
            flags[i] = 1
            for j in adjacency[i]:
                if not dfs(j, adjacency, flags): return False
            flags[i] = -1
            return True

        adjacency = [[] for _ in range(numCourses)]
        flags = [0 for _ in range(numCourses)]
        for cur, pre in prerequisites:
            adjacency[pre].append(cur)
        for i in range(numCourses):
            if not dfs(i, adjacency, flags): return False
        return True

参考链接：https://leetcode-cn.com/problems/course-schedule/solution/course-schedule-tuo-bu-pai-xu-bfsdfsliang-chong-fa/

本文已收录 GitHub，传送门~^[1] ，里面更有大厂面试完整考点，欢迎 Star。

参考资料

[1]

传送门~: https://github.com/MaoliRUNsen/runsenlearnpy100

更多的文章

点击下面小程序

- END -