旋转目标检测表征新方法

简单介绍前段时间一个工作的思想：Optimization for Arbitrary-Oriented Object Detection via Representation Invariance Loss。讨论的是旋转目标表征的问题，发表在IEEE Geoscience and Remote Sensing Letters上。

论文地址：https://ieeexplore.ieee.org/document/9555916

arxiv扩展版：https://arxiv.org/abs/2012.04150

代码：https://github.com/ming71/RIDet

1. Motivation

主流的旋转目标表征方式分为两种：旋转矩形（OBB）和四边形（QBB）。这两种表征方式都存在边界越界问题和周期性问题（参考CSL论文或者下面的示意图）。

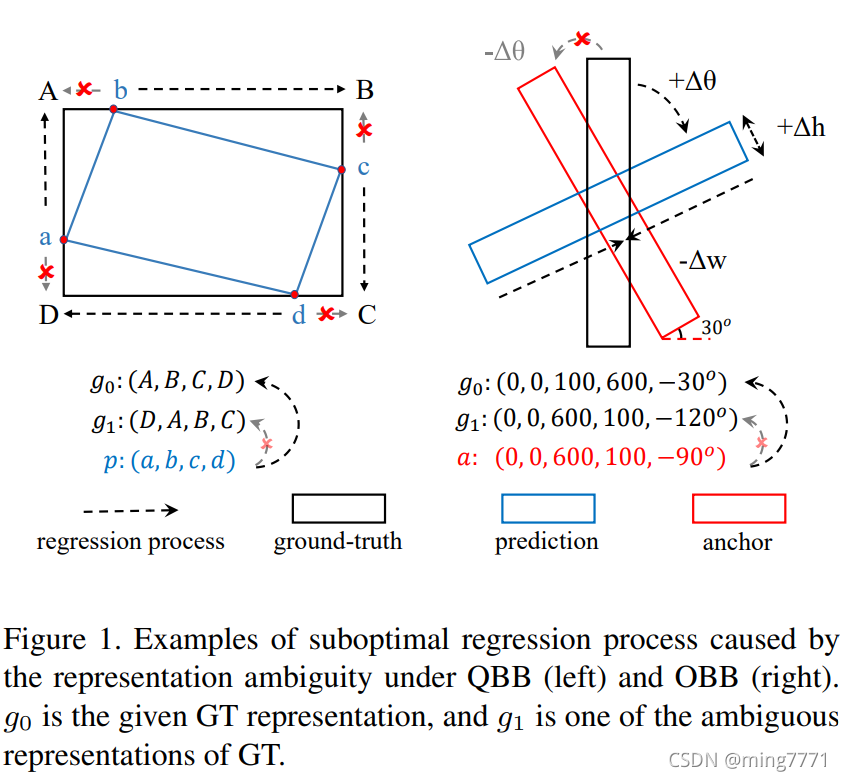
以QBB表征为例，对于一个凸的四边形而言（大多能用四边形表示的目标都是凸的），4个顶点有种组合方式，他们能表示唯一的凸四边形，这24种表示方式是等价的局部最优解。但是实际回归时，损失只能指定一种情况学习，损失向唯一的全局最小优化。

也就是说，one-to-one match的损失函数会导致次优的回归过程，损失可能震荡，收敛速度相对慢。这些多余的表征方式导致的次优学习问题本文称之为“模糊表征”问题。

同样的问题在OBB中也是存在的。之前在旋转目标检测的SCRDet，GWD等论文中提到的旋转目标表征的角度周期性（），边角互换性，实际上也是当前损失函数无法匹配到这些等价的局部极小导致的，这里就不赘述了。

2. Method

2.1 Analysis

“模糊表征”带来的旋转目标表征的歧义性在一些之前的论文中有被提到。例如SCRDet采用IoU-smoothL1损失用IoU加权来抑制越界的角度；GWD采用高斯分布的椭圆拟合来近似表征旋转矩形；或者直接把角度回归转为分类来避开这个问题。

但是这些方法都是把“模糊表征”视作旋转目标检测的一个“问题”。

实际上根据定义来看，他们同样是有效的表征方式，等价的局部极小点，直接抑制多样表征来规避问题不是最可取的。

宜疏不宜堵，更好的办法是直接让损失函数能够同等地对待这些局部极小进行更好的优化，就能够将这个问题转化为加速收敛的工具，这也是本文的初始想法。

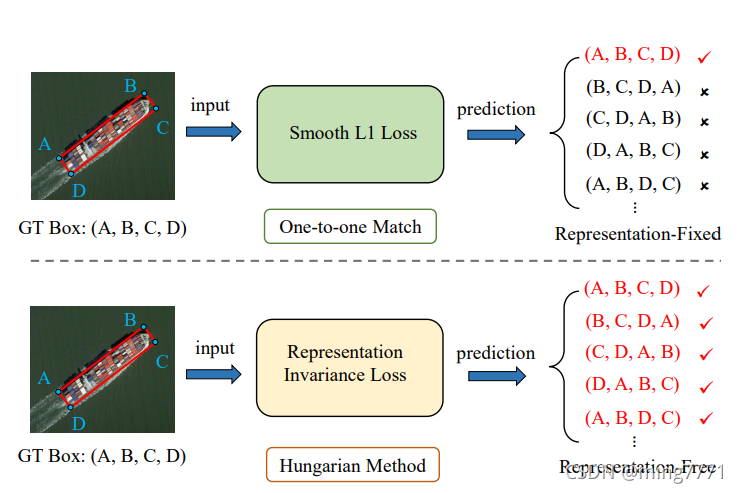
首先想到的就是匈牙利算法。匈牙利匹配很早之前就提出了，最近在DETR中又火了起来。在DETR中他解决的是prediction set和gt set之间的损失计算问题。

那么同样在这里也可以迁移过来，只要predict能够匹配到等价表征的GT set中的某一个元素即可认为成功。

基于这个思路，利用匈牙利损失，将定位过程视作集合之间的匹配即可优化回归。

2.2 RIL for QBB

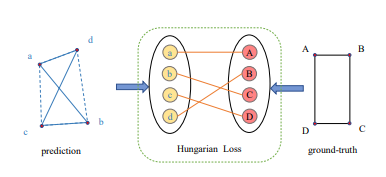
首先是用于多边形匹配的表征不变性损失。上面的思路就是按照QBB举例展开的，因此不难理解，直接将GT的四个点的组合视为GT set，然后让预测的固定四个点和其匹配即可。公式表示如下：

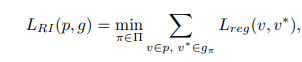
2.3 RIL for OBB

OBB中由于边角的交换性和角度的周期性，依然存在模糊表征的问题，所以同样可以将这些等价表征集视为学习的目标。

但是由于角度的周期性，这个GT set是无穷大的，实际操作中肯定不能直接匹配。因此需要对其进行优化。

这里将角度的偏离映射为类似IoU的一种度量，摆脱了周期性的问题，从而能够用到匈牙利匹配算法。如下图所示：

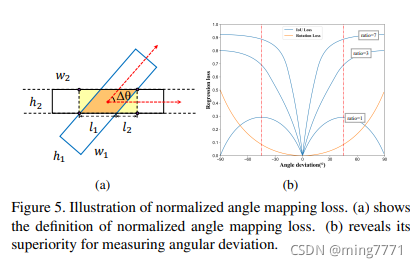
则角度损失可以转化为：

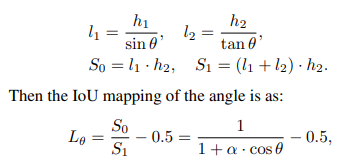
实际使用时发现这个新角度损失对其加权系数比较敏感，导致参数不好调。为了归一化不同变量之间的影响，同时对距离和尺度（即中心点和宽高的偏移）变量也做了归一化：

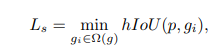
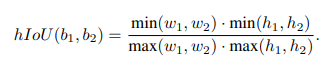
3. Experiment

本文采用了两个遥感的数据集，实际上完整版的论文采取了四个数据集：三个遥感数据集DOTA，HRSC2016，UCAS-AOD和两个个文本检测数据集ICDAR2015，MSRA-TD500。

GRSL篇幅只有5页，很多实验没展开，包括DOTA数据集的完整对比结果也没有给上，可以参考arxiv版本的获取更详尽的数据和实验。

采用的baseline模型是自己搭建的一个带refine的retinanet以获得好点的效果，避免又被喷为什么ablation性能不能吊打sota，模型如下所示：

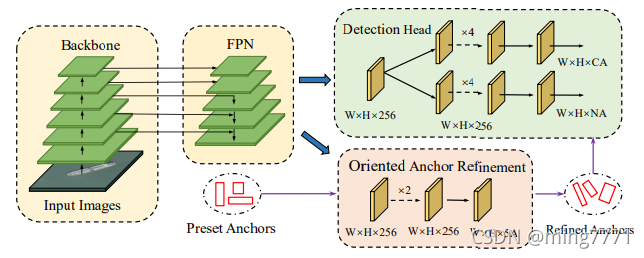
3.1 Ablation Study

3.1.1 Evaluation of normalized rotation loss for OBB

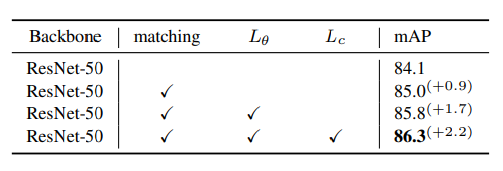
这里分别做了的实验三部分的实验：匹配策略、角度归一化、以及中心距离的归一化。

首先只有匹配策略的时候角度是无穷的，按照上文说的没法穷举所有的 可能极值，所以这里只做了2pi内的约束，相当于加了几个近的等价极小值，取得小幅度的提升。

然后是加了角度归一化的损失，进一步性能提升了1.7。看上去好像是这个角度映射挺好使的，实际上他的增益是为匹配策略服务的。证据就是单独使用这玩意的时候不好调，性能有时候还下降。

最后是中心约束能够获得更好的效果，这一点在很多相似的工作中也有得到证明。

3.1.2  Evaluation on different models

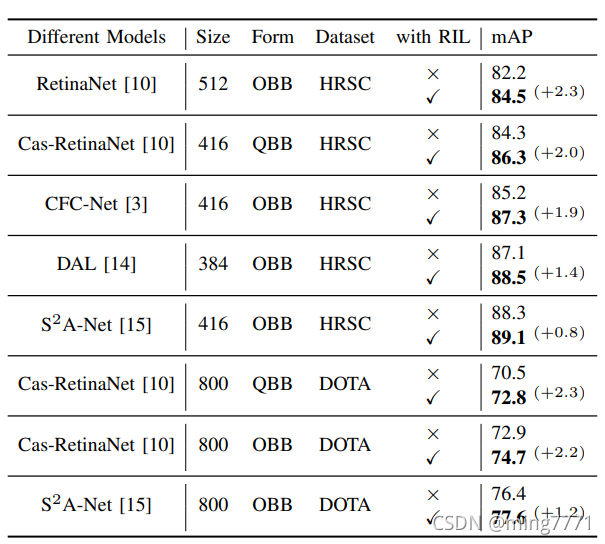这部分的实验在HRSC和DOTA上进行，切换了不同的模型可以证明方法的稳定提点，有的模型去掉了部分增强trick进行实验。

代码实现上一个是自己写的，还基于s2anet迁移上去了，为了在更多的方法上实验以及得到更好的效果。

值得一提的是，RIL对于高精度的检测性能提升比较好，这点在table中没有展现出来。

此外，相同的epoch下，使用了RIL的模型的收敛速度更快，如下图可视化结果所示。还画过一个mAP曲线也能印证这一点。

3.2 Main Results

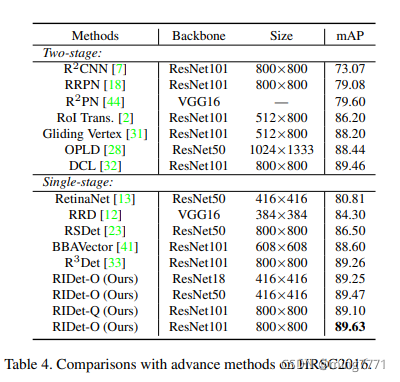
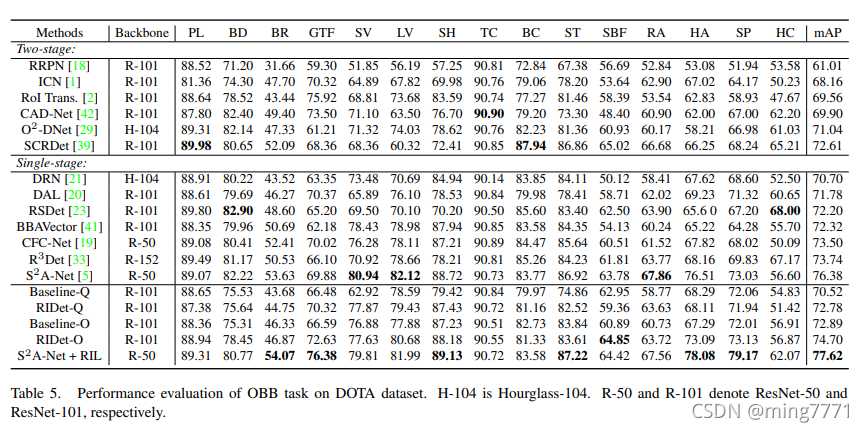
由于论文篇幅的原因没给出DOTA的详细数据，这里附上HRSC和DOTA实验结果的全表：

然后附上一些检测结果：

代码和权重都已经开源在github，有问题欢迎通过issue或者邮件联系我。