围棋中的数学原理
共 2285字，需浏览 5分钟
·
2020-07-28 15:52
日期：2020年07月26日
正文共：2030字4图
预计阅读时间：6分钟
来源：算法与数学之美
围棋一向被誉为是人类大脑智慧的专利，围棋的走法，几乎和宇宙中原子数量相同，甚至更多，每回合有250种可能，一盘棋可以长达150个回合，共有1后面再加360个0种下法，这样的计算量，对计算机来说叫暴力计算，非常残忍而且很难实现（对数字不敏感的直接看下面的GIF图更直观。但正是因为这种深度和复杂，所以几乎每个中国人都听到的话就是，围棋可以锻炼数学思维和逻辑能力。别急，至少让我们先看看围棋中有哪些数学原理。很认真的。
围棋的思维图
围棋，起源于中国，可以说是最早产生的一种棋类。相传围棋为尧所造，已经有4000年的历史。最初围棋可能与天文有联系，后来逐步变为纯粹的策略游戏。围棋的规则很简单，可以理解为双方抢占棋盘上的空间，对弈双方谁围起的空间越大谁就获得胜利。这与如今的市场经济体系是有相似之处的。
博弈论是二人在平等的对局中各自利用对方的策略变换自己的对抗策略，从而达到取胜目的理论与方法。其最早期的研究对象就是象棋，桥牌，赌博等。所以也可以用博弈论中的方法来研究围棋。
在围棋的一些基本概念，如死活，围空，实地与势中都蕴含着数学的原理。我们来细细看过。
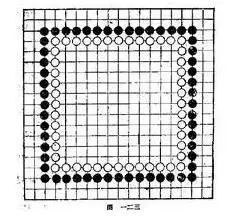
有一句棋彦叫“多子围空方胜扁”，其意思是用多颗棋子围空的时候，棋型要尽量走成方形，也就是要有立体感，要把棋子的效率最大化，这样能围城大空。扁的棋型所占目数少，子效很低，弹性小。这其实是一个约束条件下的最优化数学问题。
下棋时我们总是希望用尽量少的子围出尽量大的空。当所用的子数一样时，围空越大越好。可以近似的把这个问题抽象为一个条件极值问题：矩形周长C为定值，求矩形面积S的最大值。
即求：
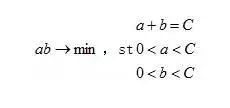
构造拉格朗日函数，
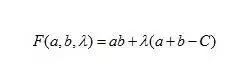
则可以列出方程：
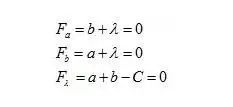
解得：
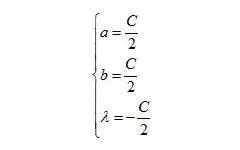
由于空的最大值在区间内一定存在，所以易得：
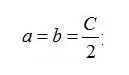
就是最大值取得的条件,也就是说矩形为正方形时围空的效率最高。有经验的棋手布局时就会注意这一点，将子下得高低错落有致，这样易于高效的围出空来，不至于下出扁平的臃肿的所谓“愚形”。
当然，关于围空效率的问题，还有很多的棋彦，比如“金角银边草肚皮”，“莫压四路，休爬二路”，“七子沿边活也输”等等，这些道理都较易明白，这里就不再赘述了。
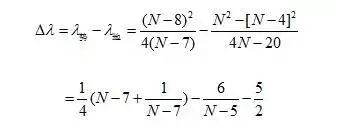
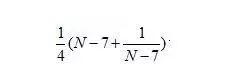
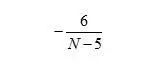
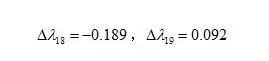
— THE END —
