图解 RNN 背后的数学原理

0引言

这篇文章的目的是对循环神经网络的功能、结构提供一个直观的认识。

一个神经网络通常取自变量 （或一组自变量）和因变量 ，然后它学习 和 之间的映射（我们称之为训练），一旦训练完成，当给定一个新的自变量，就能预测相应的因变量。

但如果数据的顺序很重要呢？想象一下，如果所有自变量的顺序都很重要呢?

让我来直观地解释一下吧。

只要假设每个蚂蚁是一个独立变量，如果一个蚂蚁朝着不同的方向前进，对其他蚂蚁来说都没关系，对吧？但是，如果蚂蚁的顺序很重要怎么办？

此时，如果一只蚂蚁错过或者离开了群体，它将会影响到后面的蚂蚁。

那么，在机器学习空间中，哪些数据的顺序是重要的呢?

• 自然语言数据的词序问题
• 语音数据
• 时间序列数据
• 视频/音乐序列数据
• 股市数据
• 等等

那么 RNN 是如何解决整体顺序很重要的数据呢？我们用自然文本数据为例来解释 RNN。

假设我正在对一部电影的用户评论进行情感分析。

从这部电影好（This movie is good） — 正面的，再到这部电影差（This movie is bad） — 负面的。

我们可以通过使用简单的词汇袋模型对它们进行分类，我们可以预测（正面的或负面的），但是等等。

如果影评是这部电影不好（This movie is not good），怎么办?

BOW 模型可能会说这是一个积极的信号，但实际上并非如此。而 RNN 理解它，并预测它是消极的信息。

1RNN 如何做到的呢?

1各类 RNN 模型

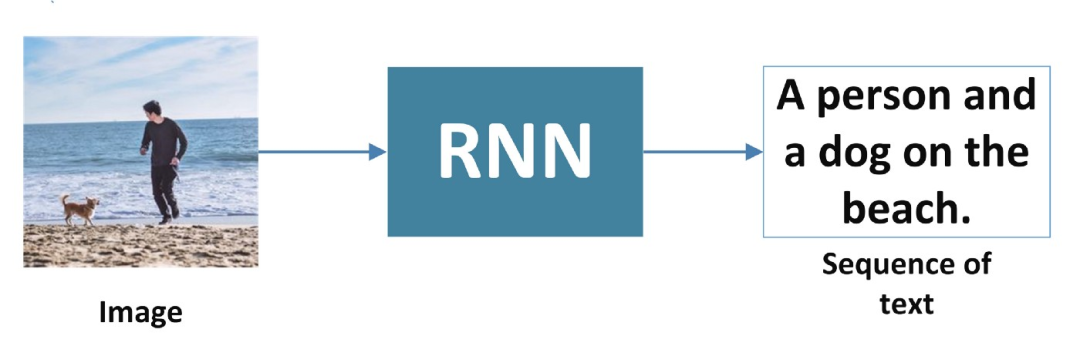
1、一对多

RNN 接受一个输入，比如一张图像，并生成一个单词序列。

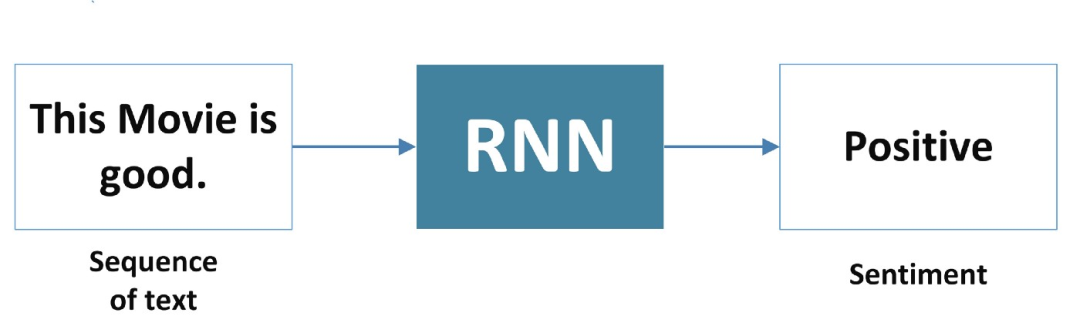
2、多对一

RNN 接受一个单词序列作为输入，并生成一个输出。

3、多对多

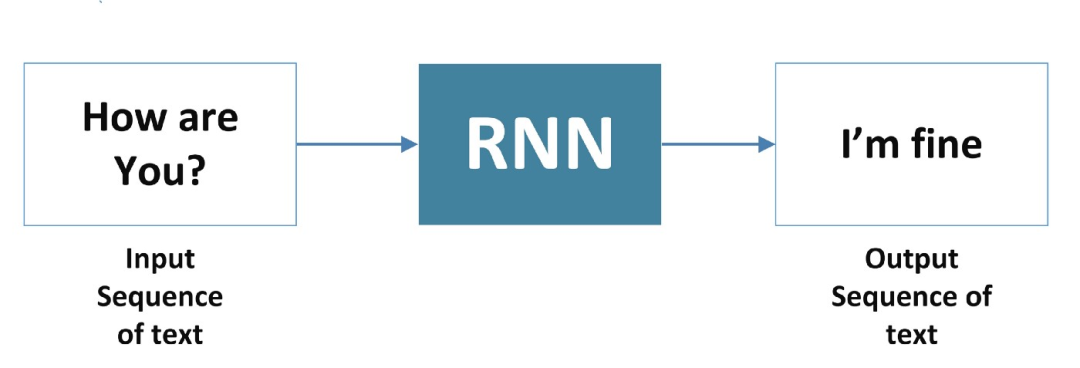
接下来，我们正专注于第二种模式多对一。RNN 的输入被视为时间步长。

示例: 输入(X) = [" this ", " movie ", " is ", " good "]

this 的时间戳是 x(0)，movie 的是 x(1)，is 的是 x(2)，good 的是 x(3)。

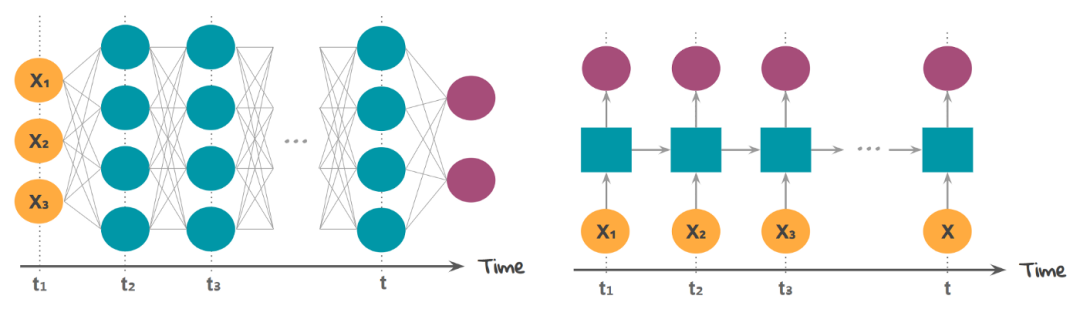
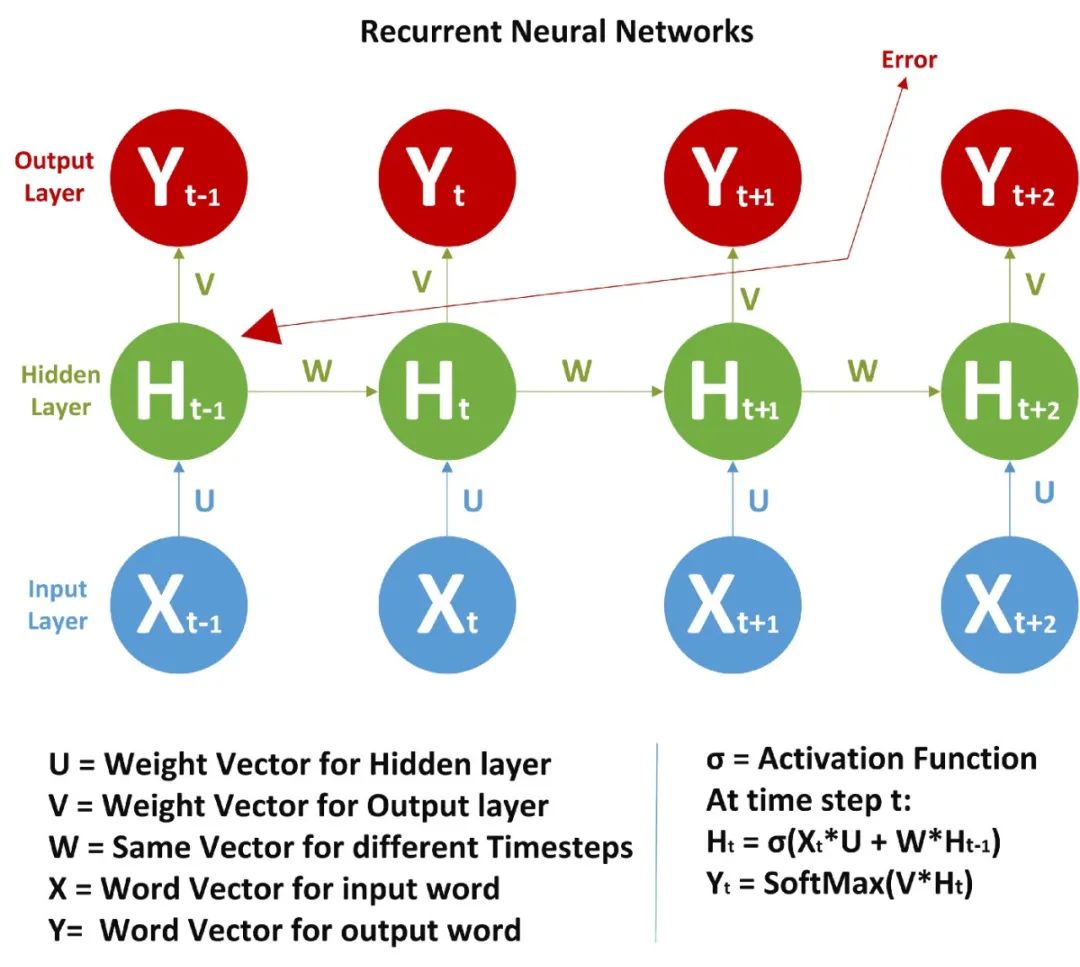
2网络架构及数学公式

下面让我们深入到 RNN 的数学世界。

首先，让我们了解 RNN 单元格包含什么！我希望并且假设大家知道前馈神经网络，FFNN 的概括，

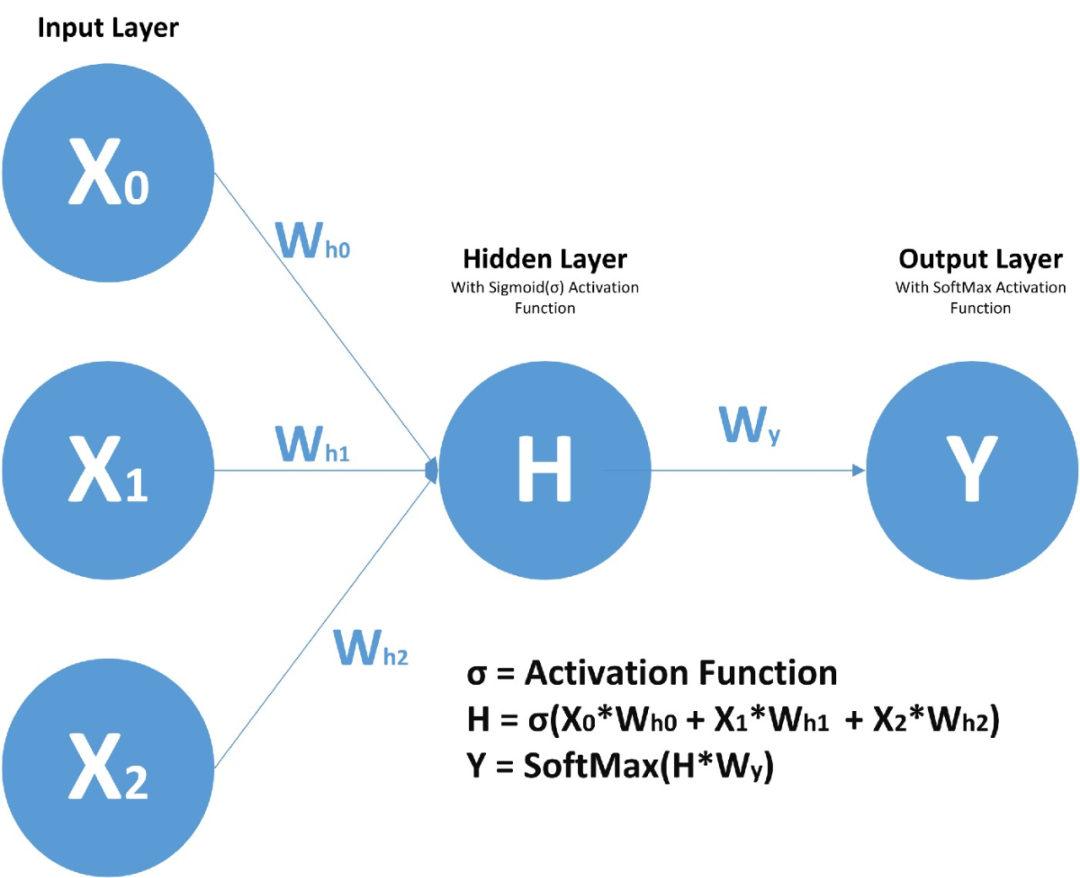
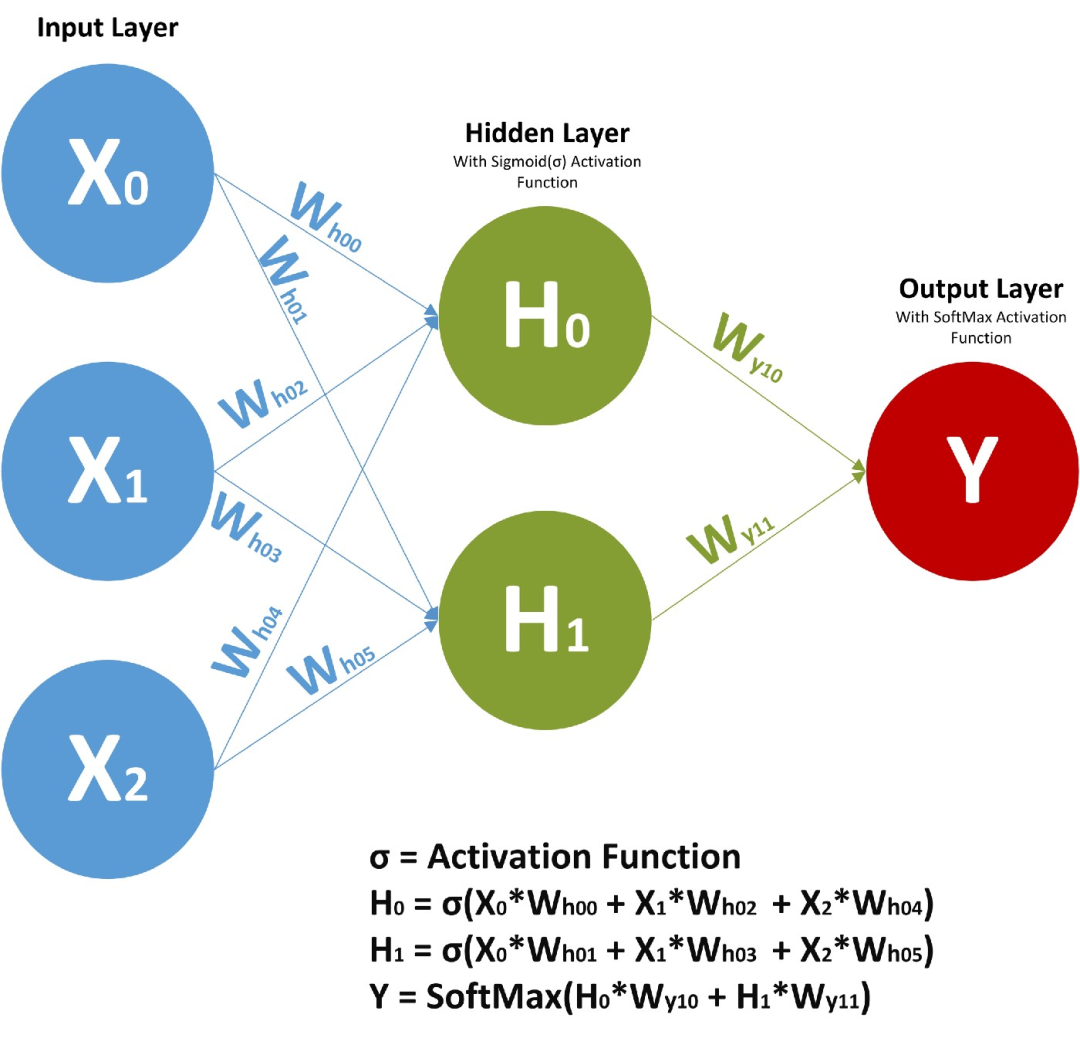
在前馈神经网络中，我们有 X（输入）、H（隐藏）和 Y（输出）。我们可以有任意多的隐藏层，但是每个隐藏层的权值 W 和每个神经元对应的输入权值是不同的。

上面，我们有权值 Wy10 和 Wy11，分别对应于两个不同的层相对于输出 Y 的权值，而 Wh00、Wh01 等代表了不同神经元相对于输入的不同权值。

由于存在时间步长，神经网络单元包含一组前馈神经网络。该神经网络具有顺序输入、顺序输出、多时间步长和多隐藏层的特点。

与 FFNN 不同的是，这里我们不仅从输入值计算隐藏层值，还从之前的时间步长值计算隐藏层值。对于时间步长，隐藏层的权值（W）是相同的。下面展示的是 RNN 以及它涉及的数学公式的完整图片。

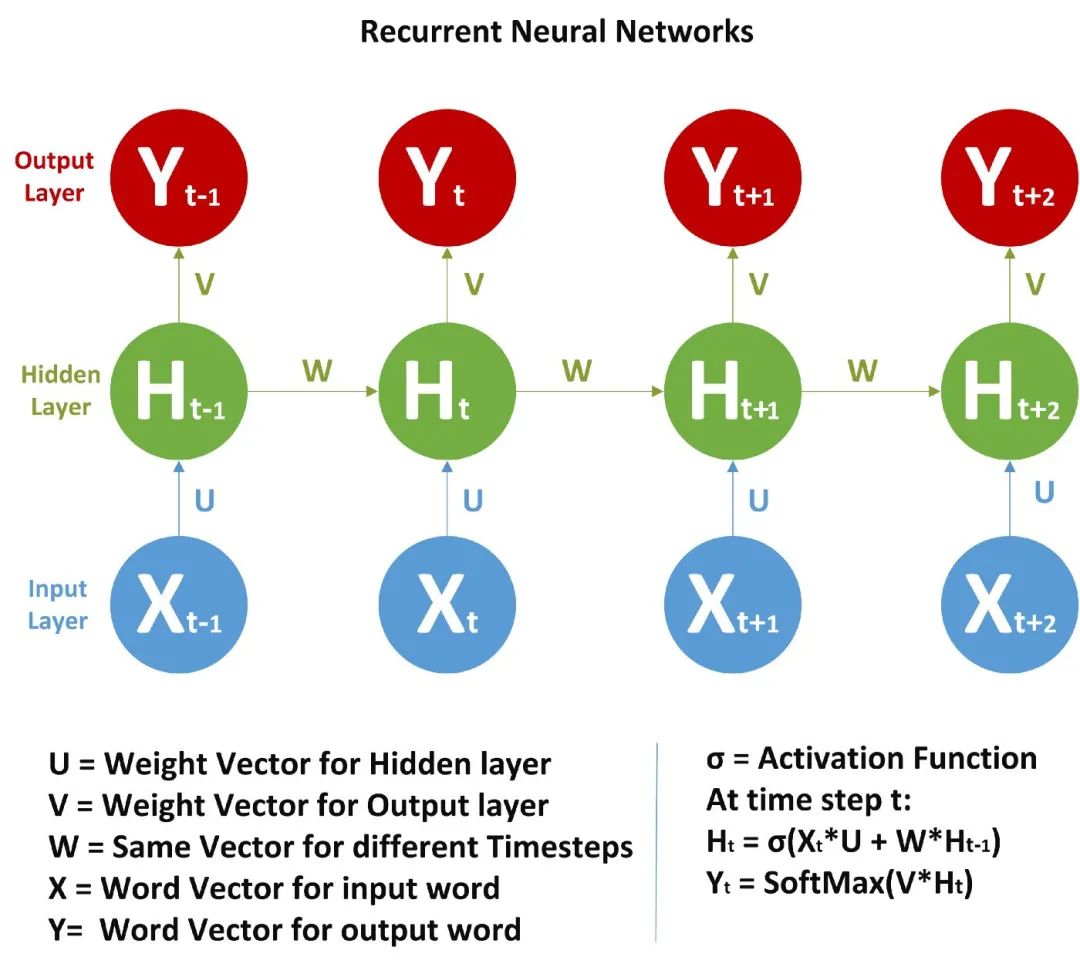
在图片中，我们正在计算隐藏层的时间步长 t 的值:

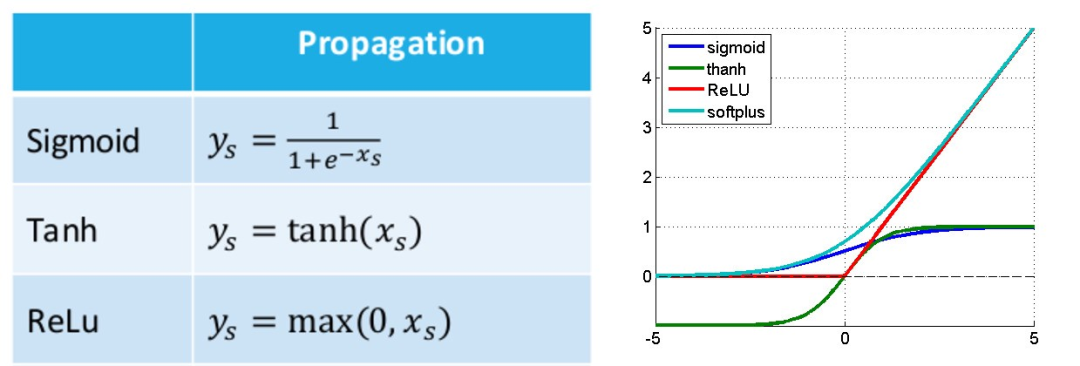
• 是之前的时间步长。我说过 W 对所有时间步长来说都是一样的。激活函数可以是 Tanh、Relu、Sigmoid 等。

上面我们只计算了 Ht，类似地，我们可以计算所有其他的时间步长。

步骤:

• 1、从 和 计算 

• 2、由 和 计算 

• 3、从 、、 和 计算 

• 4、由 和 计算 ，依此类推。

需要注意的是:

• 1、 和 是权重向量，每个时间步长都不同。

• 2、我们甚至可以先计算隐藏层（所有时间步长），然后计算 值。

• 3、权重向量一开始是随机的。

一旦前馈输入完成，我们就需要计算误差并使用反向传播法来反向传播误差，我们使用交叉熵作为代价函数。

2BPTT（时间反向传播）

如果你知道正常的神经网络是如何工作的，剩下的就很简单了，如果不清楚，可以参考本号前面关于人工神经网络的文章。

我们需要计算下面各项，

• 1、相对于输出（隐藏和输出单元）的总误差如何变化？
• 2、相对于权重（U, V, W）的输出如何变化？

因为 W 对于所有的时间步长都是一样的，我们需要返回到前面，来进行更新。

记住 RNN 的反向传播和人工神经网络的反向传播是一样的，但是这里的当前时间步长是基于之前的时间步长计算的，所以我们必须从头到尾遍历来回。

如果我们运用链式法则，就像这样

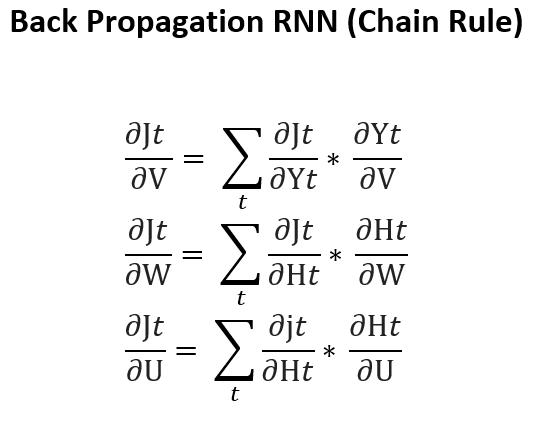
在所有时间步长上的 W 都相同，因此按链式法则展开项越来越多。

在 Richard Sochers 的循环神经网络讲座幻灯片^[1]中，可以看到一种类似但不同的计算公式的方法。

• 类似但更简洁的 RNN 公式:

• 总误差是各时间步长 t 对应误差的总和:

• 链式法则的应用:

所以这里， 与我们的 相同。

、、 可以用任何优化算法来更新，比如梯度下降法。

2回到实例

现在我们回过头来谈谈我们的情感分析问题，这里有一个 RNN，

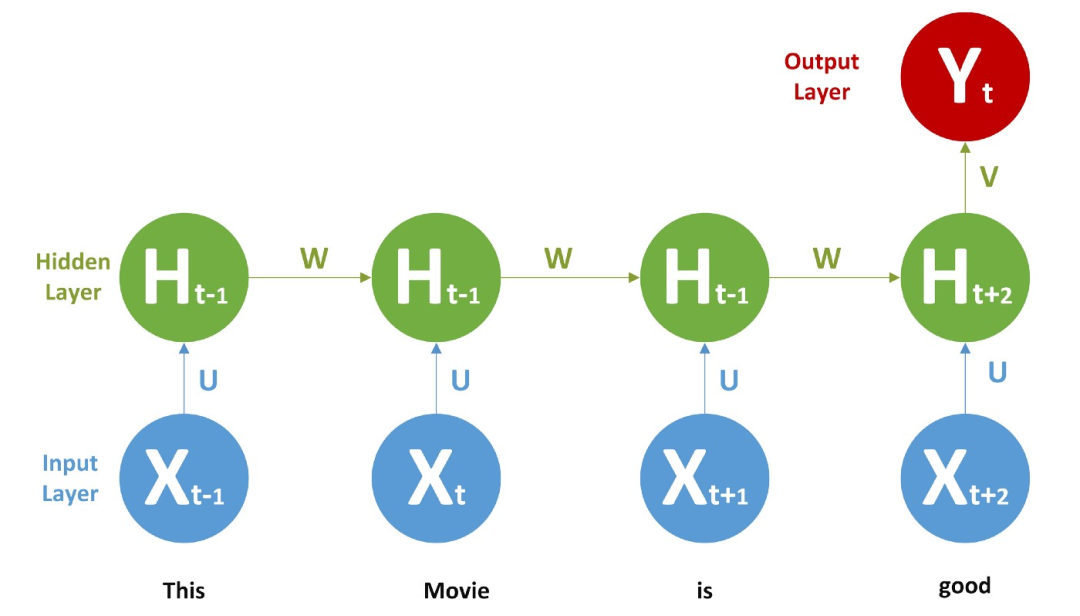
我们给每个单词提供一个词向量或者一个热编码向量作为输入，并进行前馈和 BPTT，一旦训练完成，我们就可以给出新的文本来进行预测。它会学到一些东西，比如不+积极的词 = 消极的。

RNN 的问题 → 消失/爆炸梯度问题

由于 W 对于所有的时间步长都是一样的，在反向传播过程中，当我们回去调整权重时，信号会变得要么太弱要么太强，从而导致要么消失要么爆炸的问题。为了避免这种情况，我们使用 GRU 或 LSTM，将在后续文章中介绍。

⟳参考资料⟲