【机器学习基础系列】聚类算法优缺点、使用小结
k-means
原理
优点
缺点
sklearn 调参
凝聚聚类
原理
优点
缺点
DBSCAN
原理
优点
缺点
sklearn 调参
高斯混合聚类
原理
优点
缺点
MeanShift
原理
调参
很多时候,我们在开展业务时,会很明确的知道需要挖掘哪种类型的目标客户:是否会购买产品的客户、是否会潜在流失的客户、是否是投诉用户、是否是欺诈用户等,然后针对性的做营销等。
例如,当发现某类群体是初生母亲,那么向这类群体推广母婴用品,再合适不过了。很多电商后台系统都具有类似的筛选标签功能,以精准定位待管理的用户。
实际工作中,客户往往会直接丢一堆无标签的数据过来,让你分析这堆数据的(潜在)用户有什么特征或群体属性,这时候,聚类算法就有用武之地了。
所谓物以类聚,人以群分,聚类就是要把“臭味相投“的数据(人/物)聚在一起。
聚类算法的常见应用场景:
1、客群划分:高价值客户,一般客户,易流失客户等,以使用不同的运营策略
2、推荐系统:给相似用户推荐相似商品,如”购买过该商品的用户还浏览了xxx“
3、异常点检测:即离群点判别,如金融反欺诈、网络攻击等场景;异常的数据暗示了异常的行为
聚类算法和分类预测算法的建模流程大同小异,都包括数据清洗、特征工程、模型构建、效果评估,由于聚类算法没有label作为参照物,在特征工程、效果评估上面会相对分类预测模型就显得更加麻烦,但更有意思。
下面,我对项目中经常用到的一些聚类算法做个简单的总结。
k-means
原理
k-means 可以说是最简单的聚类算法了(但是看sklearn里面的k-means算法源码实现发现并不简单orz)。
算法首先随机选取K个质心,对每一个样本,分别计算该样本到这K个质心的距离,然后将该样本归到距离最短的簇(群)中。将簇中所有样本的均值作为新的质心,再将每个样本分配到最近的簇中,一直迭代直至达到指定的迭代次数或者质心不在发生变化时,算法结束。
优点
简单直接高效 收敛贼快:算法运行效率高,(业界用的多不是没有原因的) 结果可解释性较强(效果好的情况下)
缺点
基于样本中心作为质心注定了k-means会对异常值、噪声敏感:比如一个超大个的体重拉高了群体的体重 追求类(群)内平方和最小也决定了其只能处理凸型数据,对复杂形状的数据无能为力,大多数时候聚类结果还是比较粗糙的。 无法处理离散型数据 需要指定聚类的个数(很多时候并不知道数据应该分成几类/簇/群才是最好的) 需要指定初始点(初始点的选定对聚类结果影响较大)
类/簇(cù)/群,根据上下文,指的是一个意思
sklearn 调参
class sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='deprecated',
verbose=0, random_state=None, copy_x=True, n_jobs='deprecated', algorithm='auto')
sklearn 里的kmeans 比较重要的参数有两个,n_clusters(聚类个数) 和 init(质心初始化方法)。
n_clusters的选定需要把业务和数据结合起来调整,或者你觉得这个数据大概可以分成10个类,可以从5-15类都试下,挑个效果最好的。
但有时效果最好的其业务解释性并不一定好,还有的时候将数据分成6类效果是最好的,但业务部门说了我就要5类...
init的值其实对聚类结果影响蛮大的,初始值选的不好可能无法得到有效的聚类结果。
kmeans 对init的初始化有三种方法:random,k-means++,或者传入一个ndarray向量,默认是使用k-means++方法来初始化质心,其核心思想是:初始化的聚类中心之间的相互距离要尽可能的远,一般选择默认参数就行。
凝聚聚类
class sklearn.cluster.AgglomerativeClustering(n_clusters=2, *, affinity='euclidean', memory=None, connectivity=None,
compute_full_tree='auto', linkage='ward', distance_threshold=None)
原理
凝聚聚类是一种自底向上的聚类方法:首先将每个样本当做一个聚类,然后合并距离最近或者最相似的两个类,直到满足某种停止准则。
从单个样本多个群向上聚类到几个群的过程,形象化表述为自底向上
最核心的点是在如何衡量两个类的距离或者相似度。找了些相关资料,发现定义相似度的方法还是蛮多的,这里列举几个。
单链:两个不同的簇中,离得最近的两个点之间的距离作为簇间的距离,取距离值最小的两个簇进行合并,即MIN()
全链:两个不同的簇中,离得最远的两个点之间的距离作为簇间的距离,取距离值最小的两个簇进行合并,即MAX()
平均链:每个簇中所有点之间的平均距离,取点平均距离值最小的的两个簇进行合并,即AVERAGE
方差:使得所有簇中的方差增加最小的方式合并,这通常会得到大小差不多相等的簇(对应sklearn中的ward)
优点
能够处理具有复杂形状(非凸型)的数据 无需指定聚类的个数(sklearn 中的 AgglomerativeClustering 将聚类的数量作为算法的停止准则)
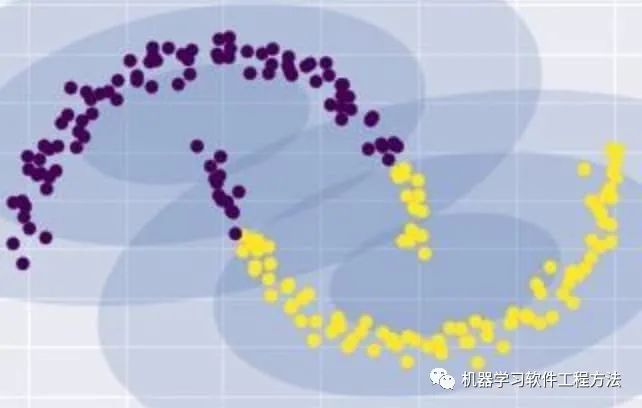
缺点
每次只合并两个簇,计算复杂度高,不适用于大数据量的聚类 只能基于已有的数据聚类,无法对新的数据进行预测,只做当前数据的观察
DBSCAN
原理
DBSCAN(density-based spatial clustering of applications with noise),翻译过来就是:具有噪声的基于密度的空间聚类应用。
它能够学习和识别数据密集区域,并将密度高的区域划分为簇,密度低的区域作为簇间的分隔。
class sklearn.cluster.DBSCAN(eps=0.5, *, min_samples=5, metric='euclidean',
metric_params=None, algorithm='auto', leaf_size=30, p=None, n_jobs=None)
优点
无需指定聚类的个数 可以处理复杂形状的数据 抗噪声,能够识别噪声点
缺点
簇之间的密度不均匀时,聚类效果可能不好。(比如某个簇,密度较大,另一个簇密度较稀疏,当调大邻域内最小样本点时,密度较稀疏的簇会变化较快。) 跟凝聚聚类一样,无法对新的数据进行预测
sklearn 调参
该算法在大多数数据集上面都能够获得不错的效果,但是调参过程有时非常坎坷。关键是目前对复杂形状的聚类评估效果并不理想。关注参数:eps,min_samples。
高斯混合聚类
class sklearn.mixture.GaussianMixture(n_components=1, *, covariance_type='full', tol=0.001, reg_covar=1e-06, max_iter=100,
n_init=1, init_params='kmeans', weights_init=None,
means_init=None, precisions_init=None, random_state=None, warm_start=False, verbose=0, verbose_interval=10)
原理
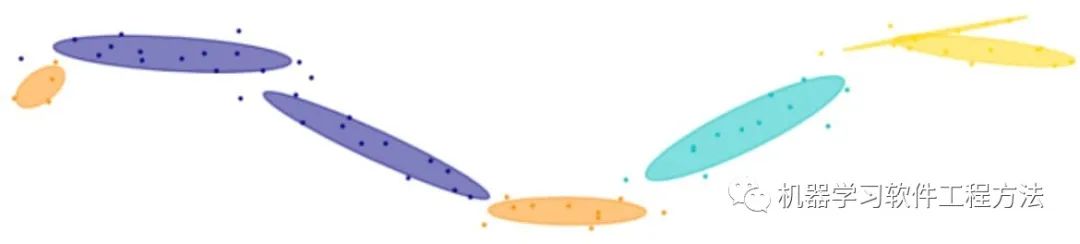
算法假定每个聚类的簇都符合高斯分布(正态分布),样本数据呈现的分布就是各个聚类的分布的叠加,所以称为高斯混合。
该算法首先指定高斯混合成分个数K(这里K就是要聚类的个数),随机给每一个分布的均值和方差(协方差)赋初始值。对每一个样本,计算其在各个高斯分布下的后验概率(EM中的E步),再根据最大似然估计,将每个样本对该高斯分布的概率作为权重来计算加权均值和方差(协方差)(EM中的M步),用更新之后的值替换原来的初始值,直至模型满足停止条件(比如迭代次数),算法结束。
优点
只要给定的成分个数足够多,理论上可以任意逼近任何连续的概率分布
缺点
计算量较大 其实真实数据好多不服从正太分布,对于一些复杂数据出现偏差的可能性还是挺高。
MeanShift
class sklearn.cluster.MeanShift(*, bandwidth=None, seeds=None, bin_seeding=False,
min_bin_freq=1, cluster_all=True, n_jobs=None, max_iter=300)
原理
MeanShift是一种非参数聚类算法,无需指定聚类的数目。主要涉及两个概念Mean(均值)、Shift(偏移)。
其算法思想很简单,首先随机选取初始迭代点,将该点到附近区域内所有点分别组成向量求和取平均偏移量,移动该点至平均偏移向量末端,作为新的迭代点,不断移动,直至满足指定条件,算法结束。
调参
MeanShift这个算法有稍微尝试了下,但是好像效果相对其他聚类算法不突出,用的不多。
高维可视化PCA、TSNE
很多时候,即使非常熟悉业务,也做了很多的数据探索,你也很难判断应该选择哪种聚类模型。
如果每个模型都试一遍的话,时间成本太高,而将(高维)数据可视化,则能指导我们选择聚类模型的方向。
数据可视化首先是将高维数据降到低维(一般二维),然后基于低维数据进行可视化,常用的方法有两种:PCA 和TSNE。
PCA是一种被广泛应用的数据压缩、数据降维方法,该方法以方差最大的方向作为坐标轴方向对数据旋转以保留主要信息,旋转后的特征在统计上不相关。
这里以sklearn里的iris数据集为例,数据属性为:花萼长度、花萼宽度、花瓣长度、花瓣宽度四个特征,将这四个特征标准化处理后用PCA降维得到下图:
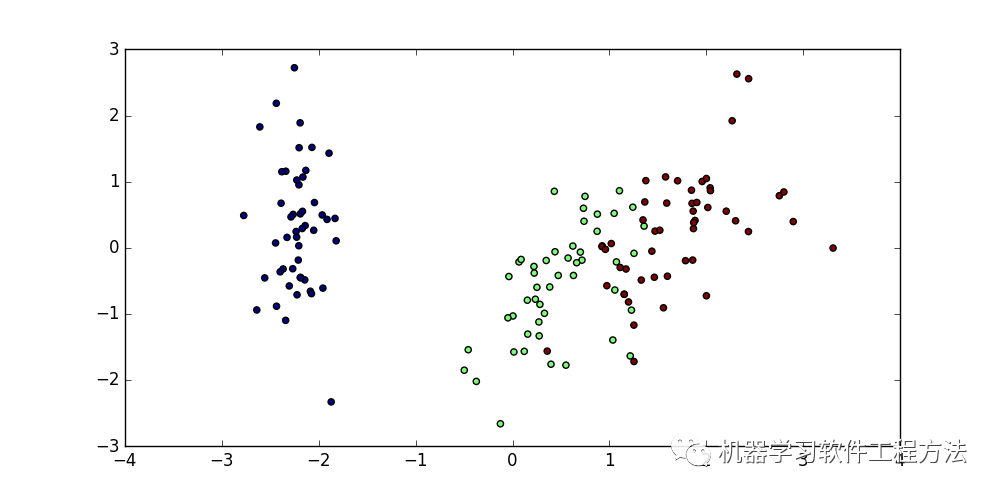
PCA在旋转时没有用到任何类别信息,降维后的数据相对于原数据相当于新的数据变换,一般很难对图中的两个轴做出解析。
还有一类用于可视化的算法称为流式学习算法,TSNE是其中的一种,降维效果奇好,其思想是找到数据的一个二维表示,尽可能地保持原数据点之间的距离,让在原始特征空间中距离较近的点更加靠近,相距较远的点更加远离。
t-SNE重点关注距离较近的点,而不是保持距离较远的点之间的距离。换句话说,它试图保存那些表示哪些点比较靠近的信息,这里同样使用iris数据进行可视化:
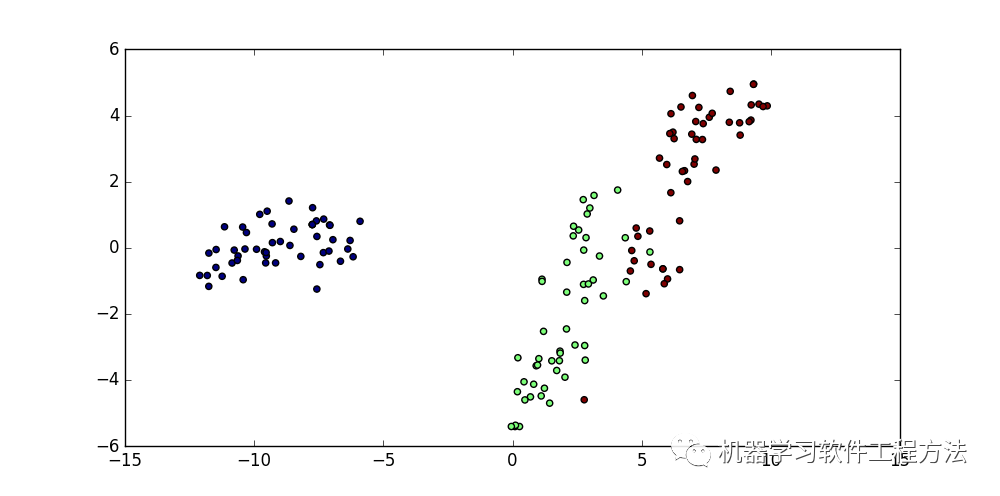
t-SNE在稍大数据量的时候效率很低。
如果要聚类的数据比较大,可以考虑抽样可视化。
如果数据形状复杂,这时候基于指标的效果评估并不好,可以考虑基于抽样数据聚类,然后基于聚类结果建立分类模型。
这里pca和tsne可视化iris数据的效果区分度不是很明显,其实从使用经验来看,数据量在千以上的情况下,同一份数据使用tsne进行可视化,数据的区分度比pca要好很多,这是因为pca需要对数据进行标准化处理,使得大部分数据都集中在一个很小的范围内,但是数据量越大tsne的处理速度越慢,很无奈。
无监督模型的特征选择
无监督模型的特征选择,sklearn上还没有相关的API,其实挺麻烦的:应该使用何种评判标准来认为这个特征是对聚类算法有效的?[本身就是无监督]
网上有一些方法,比如基于遗传算法、模式相似性判断、复相关系数之类的,也有提到可以参考有监督学习的wrapper方法进行特征选择,感觉还蛮有意思,感兴趣的可自行查找相关资料。
效果评估
聚类结果的效果评估的核心原理都基本一样,通过类内距离和类间距离判断,类内距离越小,类间距离越大说明聚类效果越好,如轮廓系数(Silhouette Coefficient)。
但不能盲目相信指标,尤其是针对任意形状的簇,虽然指标效果很差,但是实际未必。很多时候,你用某个指标评估聚类效果,如果指标值非常好,那说明模型用对了,如果指标值表现很差,那很有可能是评估方法选错了。
目前没看到靠谱的实践方法。
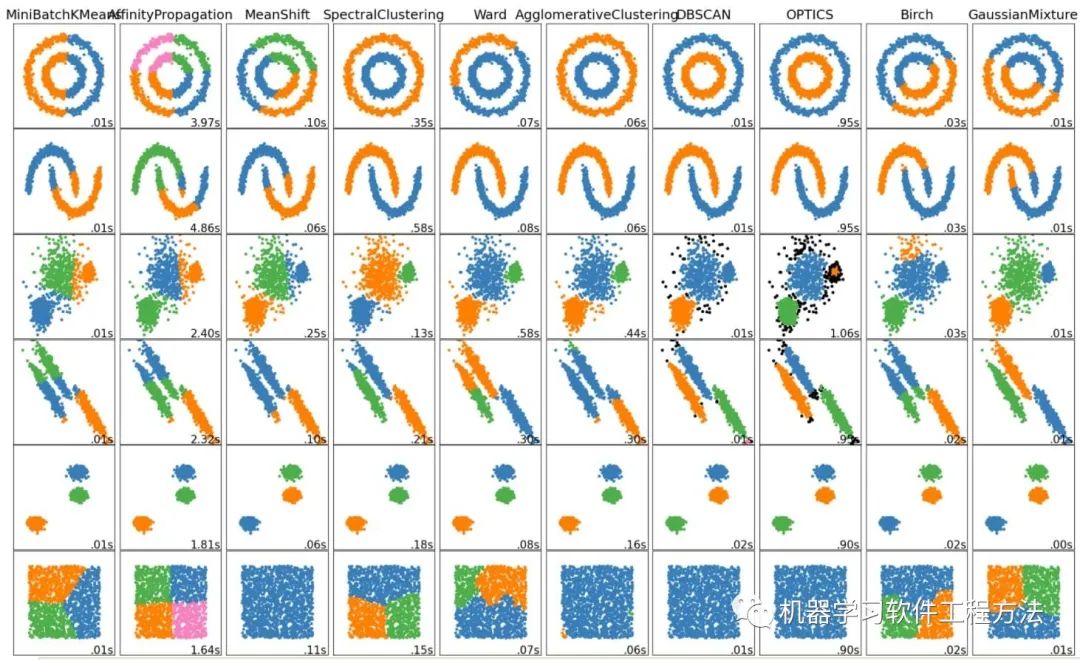
总结
参考各种算法,对聚类的效果示意图: