【机器学习基础】机器学习的损失函数小结
本文为机器学习基础 第一篇
2020这个充满变化的不平凡的一年过去了,孕育着希望和机遇的2021即将到来,在此祝愿所有朋友幸福美满,蒸蒸日上,心想事成,欢喜如意,新年快乐!
最近比较忙,好长时间没更新了,也感谢所有读者们长期以来的支持,你们的一次次阅读、分享和点赞是对我们精神上最大的鼓励和认同!技术分享不但是一种和大家知识的交流,也是一种督促自己不断进行学习的动力。通过阅读的分享和整理,能使我们对所学的知识去理解得更为深刻,也能锻炼逻辑思维的清晰度和论述叙说的准确性。所以,欢迎大家来投稿,记录自己的学习历程~
之前的预训练语言模型专题连载了十八篇,记录了当前比较热门的一些PLM的进展,之后随着学术界的发展和我们的阅读,也会继续扩充专题的规模。因为前段时间有在梳理机器学习基础,所以本期想来重温和整理一下,从损失函数开始,用三四篇文章来一起回顾机器学习的必要知识。虽然这个在网上讲得已经很多了,但还是想在公众号上搬运和汇总一下,新年第一篇,希望大家也能有所收获~
什么是损失函数
机器学习,准确地说监督学习的本质是给定一系列训练样本(xi, yi),尝试学习x -> y 的映射关系,使得给定一个新的x ,即便这个x不在训练样本中,也能够使模型的输出
损失函数是用来估量模型的输出
常见的损失函数
让我们来看一下常用的一些损失函数
0-1损失函数(Zero-One Loss)
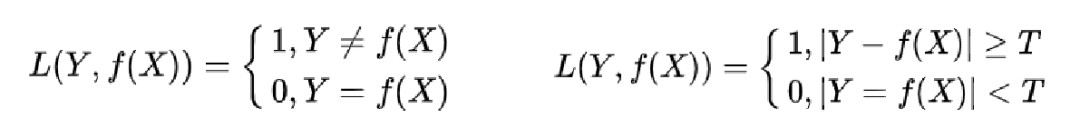
若绝对值在T以下,损失函数为0,否则为1。它是一个非凸函数不太适用
合页损失(Hinge Loss)
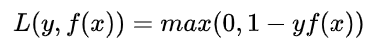
如果被分类正确,损失为0,否则损失就为
适用于 maximum-margin 的分类,支持向量机Support Vector Machine (SVM)模型的损失函数,本质上就是Hinge Loss + L2正则化
指数损失函数 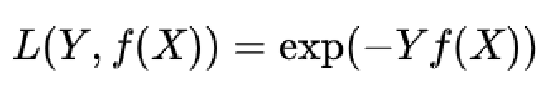
对噪声点,离群点非常敏感。
平均绝对误差损失(Mean Absolute Error Loss)
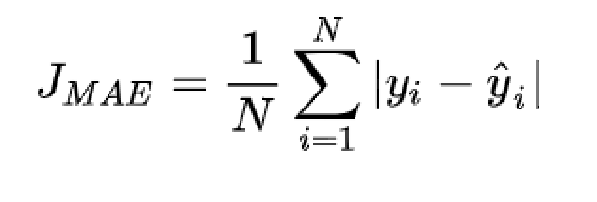
计算预测值和目标值差的绝对值,也称为MAE Loss, L1 Loss
平均平方误差损失 (Mean Square Error Loss) 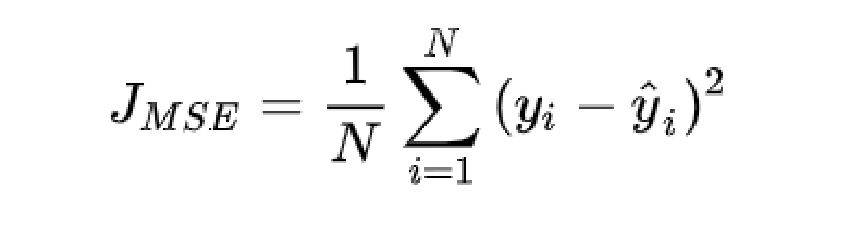
计算预测值和目标值差的平方,也称均方误差损失,MSE Loss,L2 Loss
机器学习、深度学习回归任务中最常用的一种损失函数
交叉熵损失 (Cross Entropy Loss) 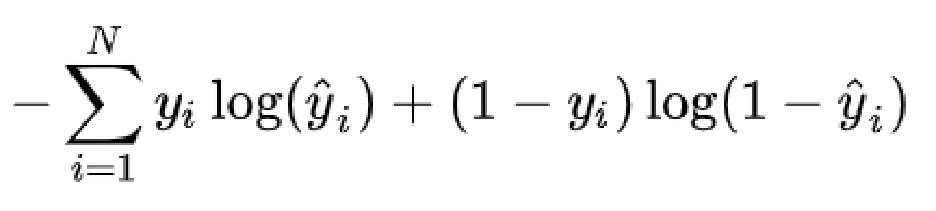
机器学习、深度学习分类任务中最常用的一种损失函数
Focal Loss 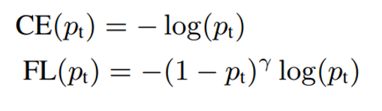
以交叉熵为基础,使模型更关注较难的样本,我们前几期有介绍过这一损失函数 Triplet Loss
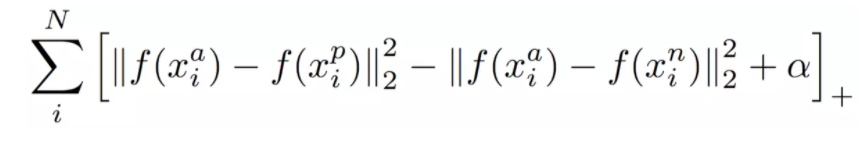
a: anchor,p: positive,n: negative
整体优化目标是拉近a, p的距离,拉远a, n的距离,达成分类效果
为什么回归任务常用均方误差损失
我们可以发现,在深度学习的回归任务中,常常会用到均方误差损失函数,这是为什么呢?
一般在生活中,如果没有系统误差,那么我们对一个数值进行估计或测量,很多情况下估计值和真值之间的误差是服从高斯分布的。我们一个模型对于目标标签的估计也可以这么认为。我们可以假设高斯分布的均值为0,方差为1。第i个样本的输入为xi , 模型的输出为yi^, 而它的标签为yi , 那么我们估计的yi的条件概率密度函数如下图所示。
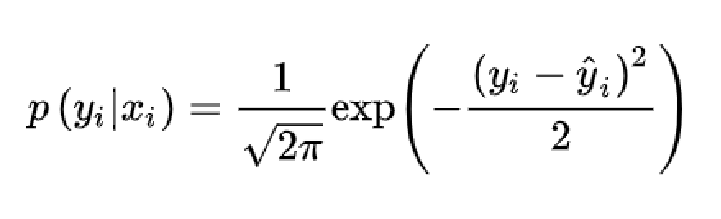
对于所有样本来说,我们可以计算出它的似然函数,我们对模型的训练就是要极大化这个似然函数。
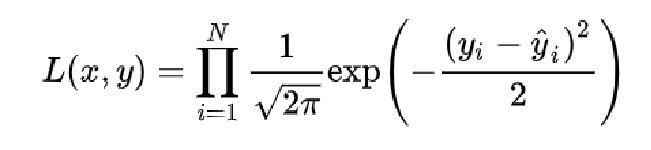
常用的做法是通过log来将比较难处理的连乘形式似然函数转换成连加形式的对数似然函数,其单调性不变。
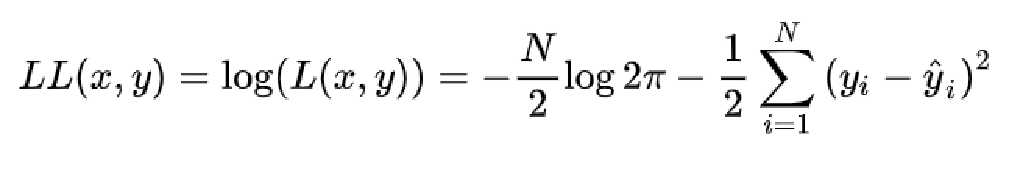
可以看到对数似然函数是负号的形式,而且第一项是一个常数,所以我们通过进一步的改写将最大化以上的对数似然函数变化为最小化以下的负对数似然函数。
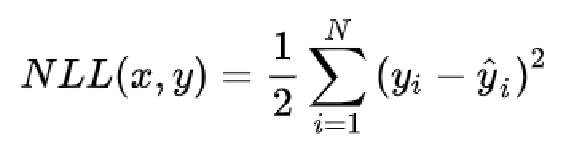
大家应该注意到了,这不就跟均方损失函数的形式几乎一样吗?正是如此,最大化似然函数和最小化均方损失函数是等价的。所以,在回归任务中,估计值和真值误差服从高斯分布的假设下,我们以均方误差作为损失函数来训练模型是合理的。
为什么分类任务用交叉熵作为损失函数
交叉熵损失函数是我们在分类任务中经常用到的损失函数,我们可以来做类似的分析。我们将要求解的问题简化为二分类,即我们使用一个模型来预测某个样本是属于分类0还是分类1,一般做法我们会去预测一个在0到1内的值yi^=p,如果大于0.5那么就是分类1,小于0.5就是分类0。
那么,在其中我们常常已经做了一个假设,即我们期望模型的输出服从一个伯努利分布。模型的输出就是预测分类为1的概率,即 P(y=1) = p, P(y=0) = 1 - p。我们将左边这个式子改写一下,在输入为x时,P(y|x) = py * ( 1 - p)(1-y)。对于所有的样本来说,将p替换成模型的预测yi^,那么其似然函数如下:
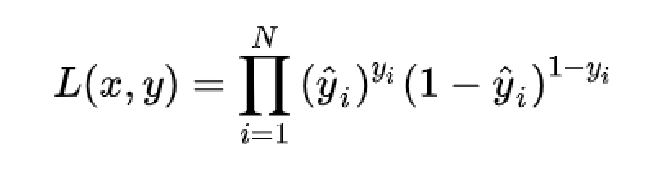
我们优化模型的过程就是极大化我们的似然函数,让模型的预测值出现的可能性最大。刚刚我们已经介绍过了,我们通过常规操作,可以将最大化似然函数的目标转化为最小化负对数似然函数。
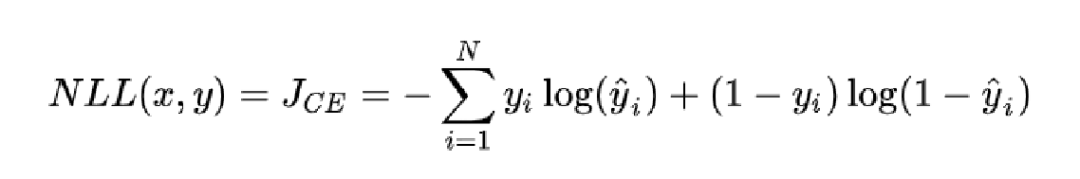
我们又能发现,这显然就是我们的交叉熵损失函数。所以,本质上对分类任务的极大似然估计和最小化交叉熵损失函数是一致的。所以,只要服从伯努利分布的假设,我们使用交叉熵处理分类任务就是很合理的。
总结
以上是我们从分布假设的角度来解释为什么回归和分类任务常常使用均方误差和交叉熵损失函数,其实我们还可以从任务的评价指标考虑来解释目标函数的合理性。但是反过来从根源上想,正是因为不同的任务有不同的分布性质和评价指标,人们才会去设计相应的损失函数去进行优化。
未完待续
本期的机器学习知识就给大家分享到这里,感谢大家的阅读和支持,下期我们还会带来新的分享,敬请期待!
欢迎关注朴素人工智能,这里有很多最新最热的论文阅读分享,也有人工智能的基础知识讨论和整理,有问题或建议可以在公众号下留言。
参考资料
1.https://zhuanlan.zhihu.com/p/58883095?utm_source=wechat_session&utm_medium=social&utm_oi=942087358187851776&utm_campaign=shareopn
2.https://zhuanlan.zhihu.com/p/97698386?utm_source=wechat_session&utm_medium=social&utm_oi=942087358187851776&utm_campaign=shareopn
往期精彩回顾
获取本站知识星球优惠券,复制链接直接打开:
https://t.zsxq.com/qFiUFMV
本站qq群704220115。
加入微信群请扫码:
