从零开始深度学习Pytorch笔记(8)—— 计算图与自动求导(上)
前文传送门：从零开始深度学习Pytorch笔记（1）——安装Pytorch从零开始深度学习Pytorch笔记（2）——张量的创建（上）从零开始深度学习Pytorch笔记（3）——张量的创建（下）从零开始深度学习Pytorch笔记（4）——张量的拼接与切分从零开始深度学习Pytorch笔记（5）——张量的索引与变换从零开始深度学习Pytorch笔记（6）——张量的数学运算从零开始深度学习Pytorch笔记（7）—— 使用Pytorch实现线性回归
在该系列的上一篇，我们介绍了使用Pytorch搭建线性回归模型，本文教会大家使用Pytorch时涉及的两个重要知识点——计算图和自动求导。什么是计算图呢？首先，在深度学习中有着图的概念，所以有边和节点，节点为张量，而边为计算过程，则为计算图，具体可以看图: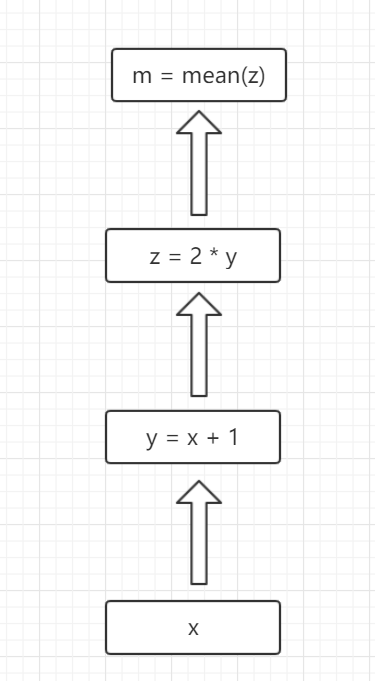
x、y、z、m 的计算关系如图所示，他们可构成一个计算图。说完计算图之后，我们来看看自动求导。
我们可以从这个计算图中看出，如果 x 为一个张量，则根据计算关系可以推出 y 也为一个张量，z 也为一个张量，而 m 是对 z 张量中的每个元素求均值，则 z 为一个标量。
当我们使用Pytorch时，经常会搭建各种神经网络结构模型，而在神经网络结构中的误差反向传播是很基础但又很实用的内容，在误差反传的时候需要求导计算，我们来看看Pytorch的自动求导。首先我们定义一个张量x，并初始化赋值。注意的地方时，我们加入了requires_grad=True这个参数，该参数使得x张量可以被求导操作。
import torch
x = torch.ones(2,3,requires_grad=True)
print(x)
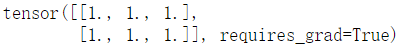然后我们通过x生成张量y。y = x + 1
print(y)
我们检查张量y，发现张量y可以求导。y.requires_grad我们来完整构建一个计算图（按照之前的计算图）。
x = torch.tensor([[1.,2.,3.],[4.,5.,6.]],requires_grad=True)然后我们m进行求导。
y = x+1
z = 2*y
m = torch.mean(z)
m.backward()然后看看m对x求导的结果，通过复合求导我们可以算出，m对x的导数为1/3的x，因为x是全1张量：
x.grad # m对x求导结果 结果为：1/3
发现计算结果和代码运行结果一致！如果我们使用中间变量z求导，如下所示。
z.backward()
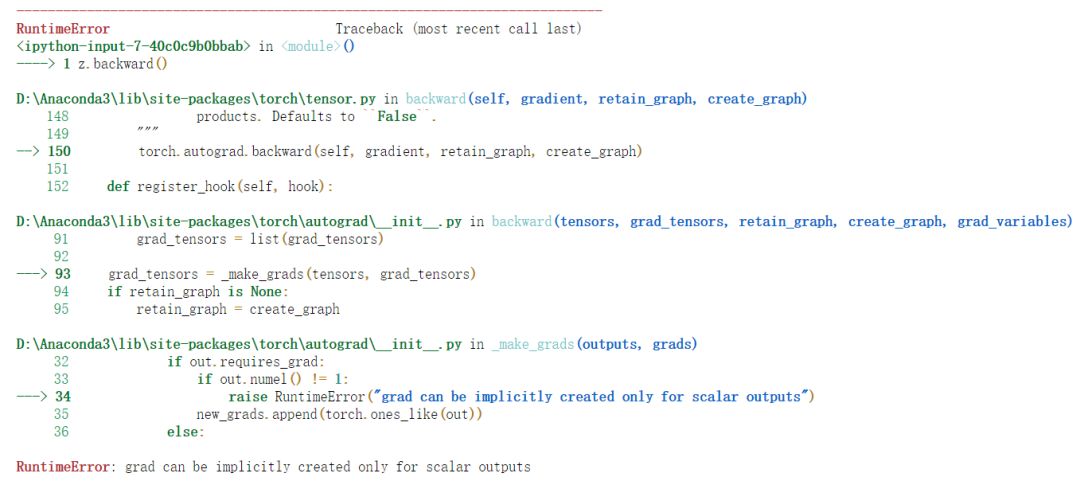结果会有异常，这是因为默认情况下，求导的操作只能是标量对标量求导，或者是标量对向量/矩阵求导！其实，也可以使用非标量（向量/矩阵）对其他张量求导，只需要研究backward的方法参数即可，但是一般的神经网络误差反传场景下，我们的误差通常是个标量，所以掌握标量的求导已经够用啦~还有一点比较重要的是，一个计算图默认情况下只能backward一次。
m.backward()#当我们尝试再次使用backward
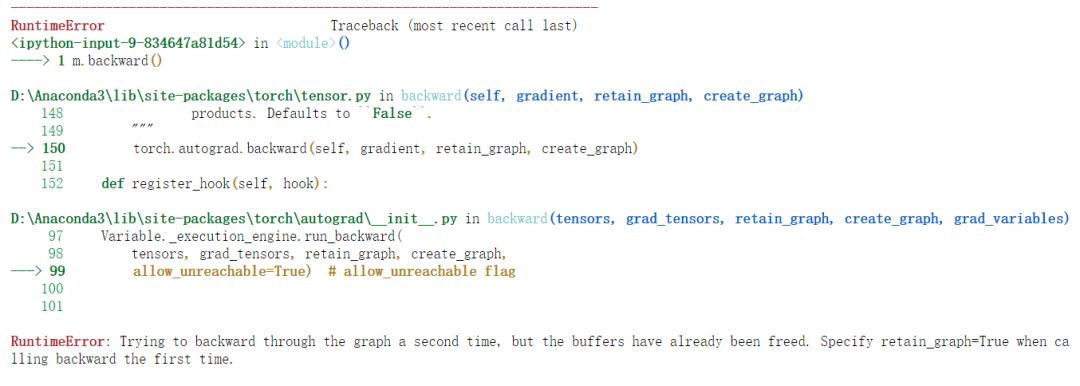仔细看抛出的异常：RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.大概意思是：你第二次再backward的时候，计算图已经销毁了，如果需要多次backward，你需要在第一次backward的时候，加上retain_graph=True的参数。所以反向求导会让计算图销毁，主要是为了节约内存，你想想，我们的深度学习网络这么复杂，训练时要在网络中不断正向和反向传播，会计算n多次求导，是不是会很占用内存呢？我们尝试重新建立计算图！x = torch.tensor([[1.,2.,3.],[4.,5.,6.]],requires_grad=True)这样在第二次backward求导就不会出问题啦~
y = x+1
z = 2*y
m = torch.mean(z)
m.backward(retain_graph=True)
m.backward()
喜欢记得点在看哦，证明你来看过~评论