引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不适用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。

本系列文章首发于微信公众号：JAVA&NLP

本文介绍自动求导的基础知识——计算图。

计算图

我们知道，反向传播是模型训练的途径。而反向传播是基于求导的，有没有想过像Keras和PyTorch这种工具是如何做到自动求导的。答案就是计算图，只要掌握了计算图的知识，我们就能自己开发一个自动求导工具。

计算图是一种描述函数的工具，可以可视化为有向图结构。其中节点为Tensor(向量/张量)，有向边为操作。

在深度学习中比较常见的例子是类似

x可以看成是输入，y可以看成是输出，中间经过了3次变换。

有时我们的函数有多个参数(比如乘法就有两个参数)，假设我们要计算，它的计算图如下：

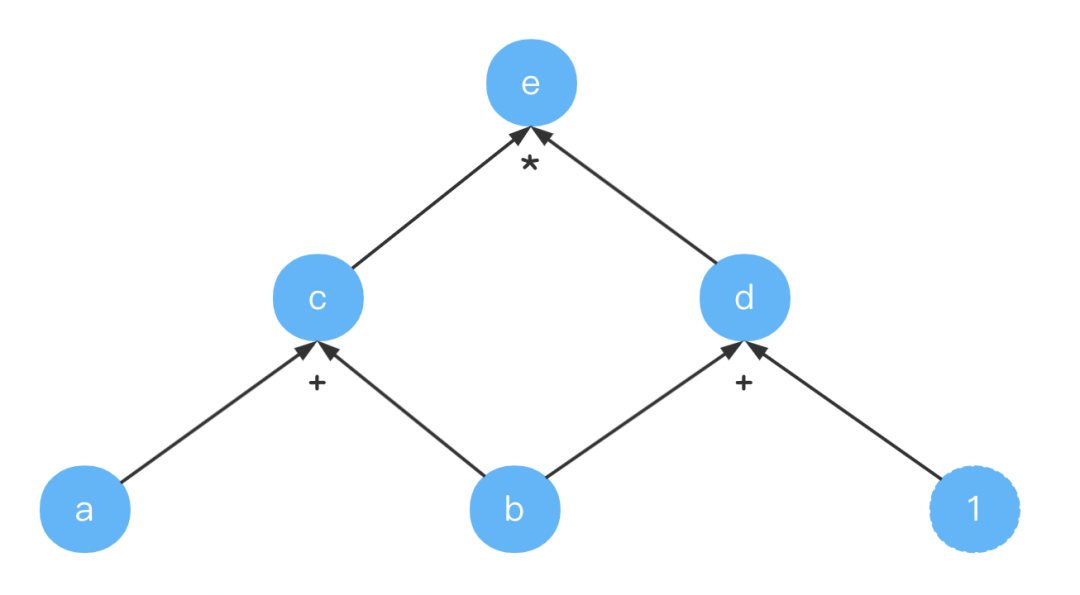
这里令，为了完整性，也画出了常量。

有了这个计算图，我们就就可以很容易的计算出的值。比如令

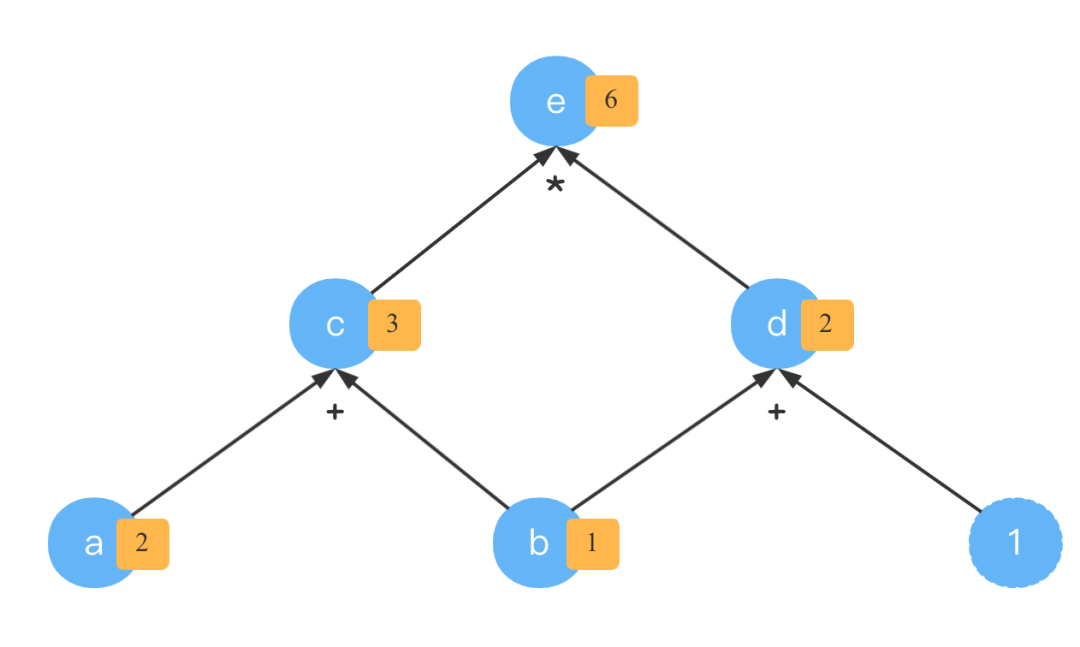
当然，我们这么辛苦的画出这个图，主要不是为了沿着箭头方向进行计算的。而是为了求导，也就是计算梯度。

计算图上的梯度

回顾一下链式法则

我们重点来看下多路径的链式法则，即上面说的全导数。

我们要计算中。

。

类似上图中的，也影响了两个因子。因此有

要计算偏导数，我们先把每个箭头的偏导数计算出来。

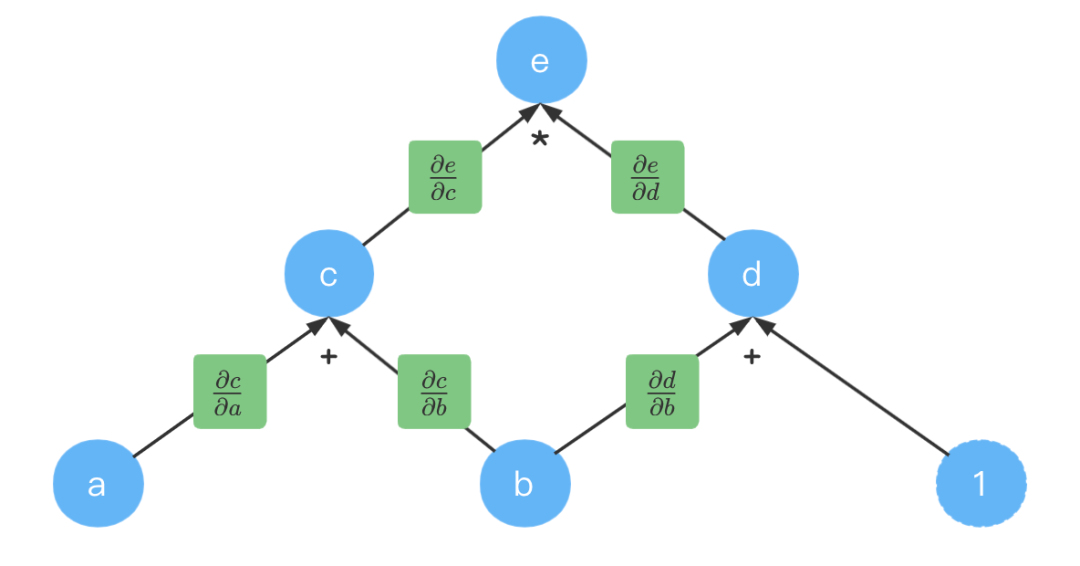
我们先填入计算出来的式子：

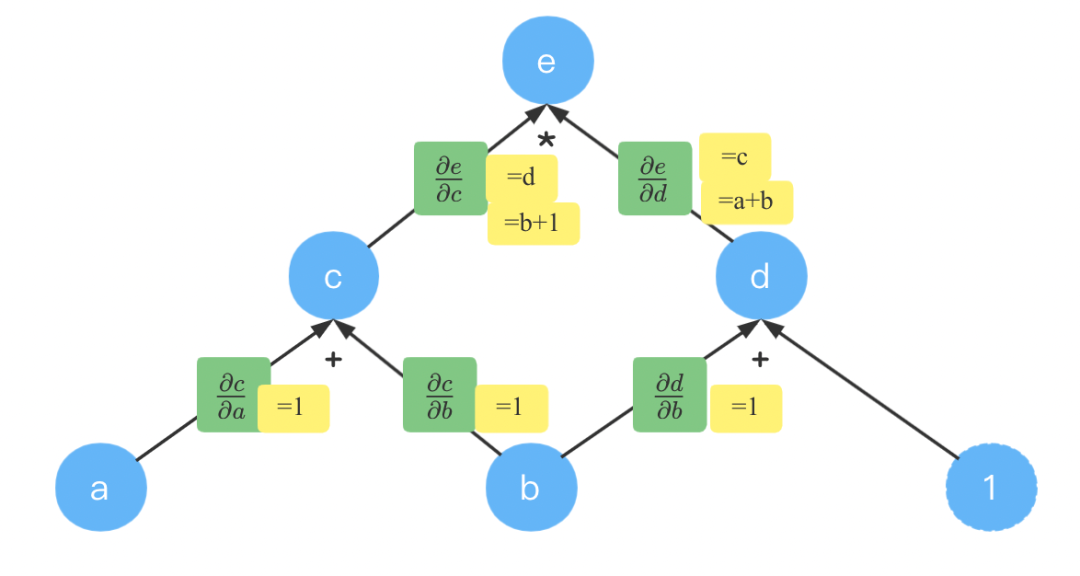
根据以及求导公式不难得到上面的结果。

此时，要计算，只需要找出所有从到到路径，然后把相同路径上的值相乘，不同路径上的值相加(连线相乘，分线相加)。

就可以得到：

此时，代入。

先计算出，再计算，所以

反向模式

如果要同时计算对和的偏导数，我们需要反向模式(Reverse mode)来同时计算它们。

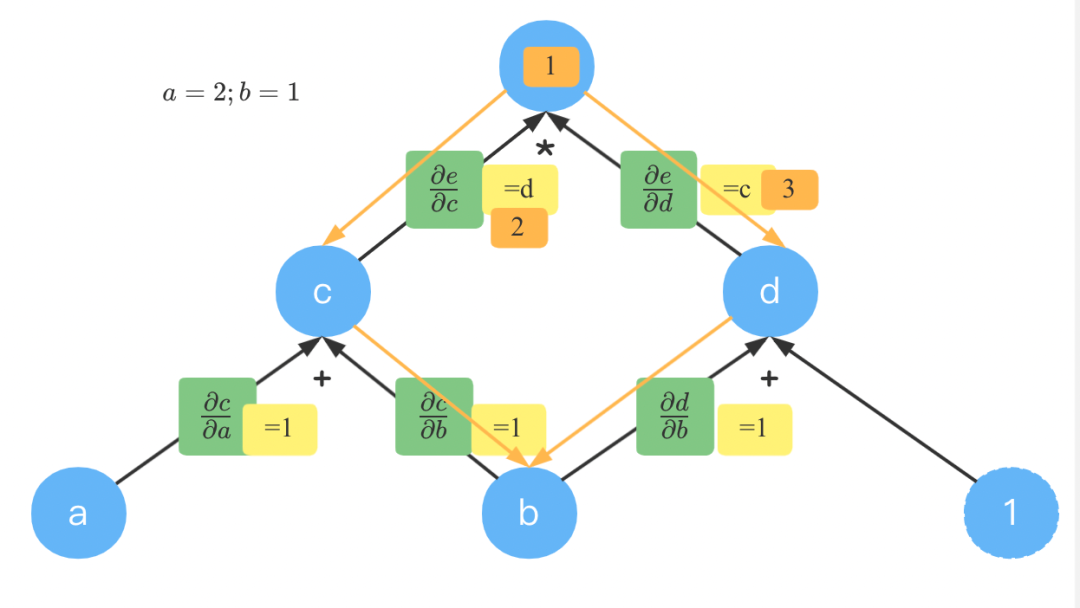
反向就是从顶点开始，这里从开始，也从梯度等于开始。

从顶点到，通过有两条路径，如山古同橙色箭头所示。达到时的梯度为；到达时的梯度为。

和到的梯度都是。根据相同路径相乘，不同路径相加。到到梯度为。

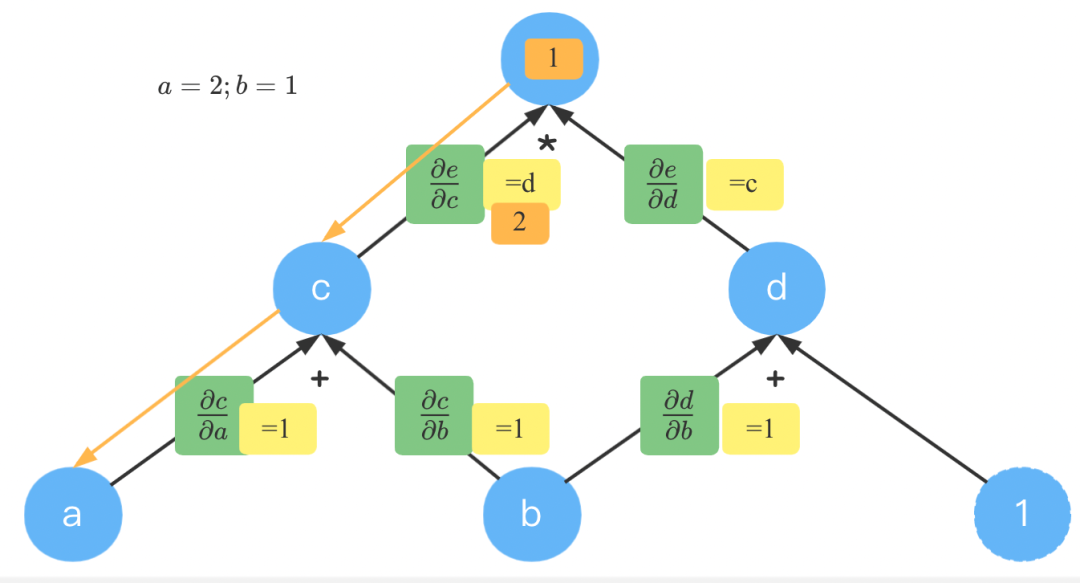
此时，计算到的就简单了，我们已经知道了到到梯度为，由于到只有一条路径，因此直接相乘得。

如果你的函数只有一个输出，由需要同时计算大量的不同值的偏导数时，用反向模式就比较快。

而这恰恰非常适合于我们计算损失函数的梯度，因为损失函数的输出就是一个标量。