​联邦学习下的安全矩阵分解 | 2021 WAIC 论文分享

点击上方“视学算法”，选择加"星标"或“置顶”

重磅干货，第一时间送达

7月8日，为期三天的2021 年世界人工智能大会（WAIC）于上海世博展馆拉开序幕。本届大会继续秉持「智联世界」的理念，以「众智成城」为主题，集聚全球范围内的人工智能创新思想、技术、应用、人才和资本，推动全球科技的创新协同。8日下午，星云Clustar受邀出席同期举办的「2021 WAIC· 隐私计算学术交流会」，并进行了基于联邦学习的安全矩阵分解框架的论文分享。 

论文分享的题目是《Secure Federated Matrix Factorization》，该论文基于联邦学习环境，首创性地提出了名为「FedMF」的安全矩阵分解框架。框架首次从数学上验证了矩阵分解在横向联邦学习中交换梯度明文信息会造成隐私泄露，并提出了使用同态加密对梯度信息进行保护的解决方案。

本文第一作者为香港科技大学计算机博士在读、星云Clustar算法工程师柴迪；北京大学助理教授、博士导师、星云Clustar首席AI科学家王乐业（按姓氏拼音排序）；第二作者为香港科技大学教授、星云Clustar创始人陈凯；第三作者为香港科技大学教授、微众银行首席人工智能官杨强。论文已发表在IJCAI 2019 Federated Machine Learning Workshop，IJCAI国际人工智能联合会议是全球人工智能领域最权威的学术会议。

在论文中，星云Clustar团队证明了传统的矩阵分解推荐系统中，当用户将梯度信息以明文形式发送到服务器，仍有泄露用户的评分信息、特征向量等信息的可能性，进而暴露用户的年龄、性别、地址等等隐私数据，造成难以预估的严重风险。

为此，星云Clustar团队设计了一个用户级的分布式矩阵分解框架FedMF，采用同态加密来增强该分布式矩阵分解框架，并用一个真实的电影分级数据集对其进行了测试。通过测试，这套框架规避了传统矩阵分解推荐系统暴露用户隐私数据的风险，采用同态加密大幅增强了矩阵分解框架的安全性，并实现了与原始数据相比一致的精确度。 

据悉，FedMF已经成功落地于全球首个工业级联邦学习开源框架FATE。星云Clustar合作设计了基于FedMF安全矩阵分解框架的联邦推荐算法（FedRec），该算法在FATE框架中的有效运用使得联邦学习在推荐系统的应用更加明确化。同时，FedRec广泛支持各种推荐场景，对于开发者而言，可以显著提高产品分发效率和算法预测效果，优化用户体验，还可解决数据不足和标签短缺等问题。

以下是由星云Clustar团队带来的《Secure Federated Matrix Factorization 》论文解读：本文围绕6个角度来讲述这篇论文，研究意义、先行概念、分布式矩阵分解、联邦矩阵分解、实验评估结果、下一步研究方向。

1

研究意义

以General Data Protection Regulation为代表，政府开始出台各类规章和法律条文，用来加强对隐私性数据的保护力度，学院机构以及工业企业也因此开始关注隐私保护机器学习这一技术领域。目前推荐系统是一个广受关注的研究课题，矩阵分解是常见的技术手段。

然而，传统的矩阵分解推荐系统，会泄漏用户的评分信息、特征向量，可能大家会觉得泄漏这两种信息不重要，但是通过这两种信息，恶意攻击者可以进行inference attack，也就是从这两种信息推断用户的性别、年龄、住址，而后面的这些信息都属于非常隐私的数据。

目前针对这类问题，主要有两种解决方案：Obfuscation-based和Full-Homomorphic encryption-based。前者主要采用的方法是通过将用户的原始偏好数据进行混淆后，再发送到中央服务器，以实现某种程度上的隐私保护。显而易见的是，这种方法会导致预测精度的损失。

为了保证预测精度，Full-Homomorphic encryption-based方法引入了一个第三方的私密服务提供商，然而这种方法会增大系统实现难度，同时这类私密服务提供商的可靠性难以保障，一旦他们与推荐服务节点存在不正当合作关系，那对用户来说，任何信息都毫无隐私可言。

2

先行概念

在正式介绍我们的方法前，首先需要了解2个概念：

Horizontal Federated Learning：用户的特征空间相同，然而用户群体不同。这类问题下，我们一般规定，用户是诚实的，系统的目标是保护用户的隐私，免于受到诚实但好奇的服务器的侵犯。

Homomorphic Encryption：一种仅享有数据处理权，但不具备数据访问权的方法。换句话说，这种方法允许任何第三方对已经加密过的数据进行运算，而不可以在运算前对数据进行解密。

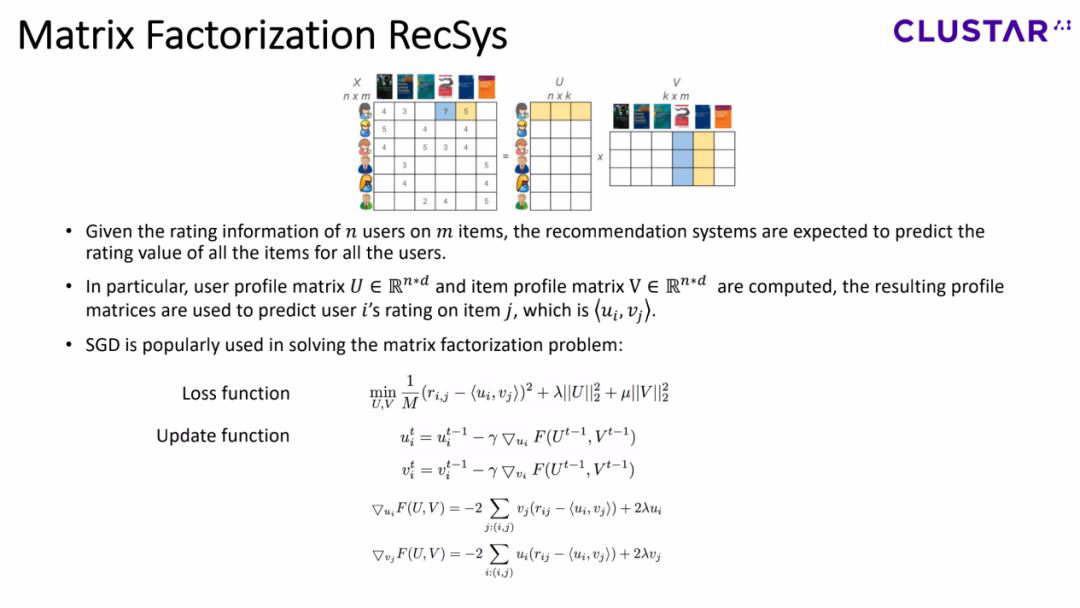
在矩阵分解推荐系统中，我们通常会拿到一个稀缺的用户评分矩阵 X，而我们的任务是通过计算出user profile 矩阵U和item profile矩阵V，来将X中的空缺信息补全。一般来说，SGD（Stochastic Gradient Descent，随机梯度下降）是用来解决矩阵分解的主流方法。具体loss function和updating formula的定义如图所示。

3

分布式矩阵求解

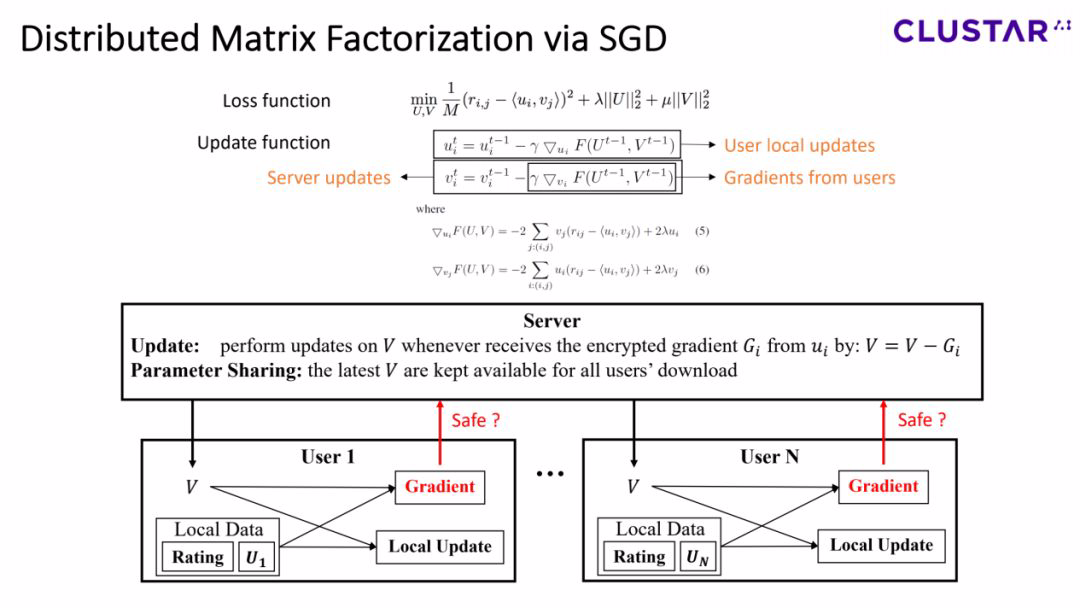
显而易见的，想要保护用户的隐私，就是将服务器与用户的数据进行隔离，避免服务器对用户数据的直接访问，所以我们希望用户可以把自己的数据保留在本地。

基于此，我们设计了一个分布式的矩阵分解系统，在这个系统中，所有的评分数据都掌握在用户手中。一个全局的item profile矩阵为所有用户提供一个本地的update，同时用户将会把gradient传回给服务器，用来更新item profile。总结来说，服务器只会收到用户的gradient，不会收到用户的任何评分信息。

这样看来，我们的任务目标就实现了，但是让我们再思考一个问题，传输gradient就真的能保障用户隐私了吗？

如果已知任意2个连续step的gradients，已知user profile的更新公式，我们可以求得一个多元高阶方程组7、8、9。求解这个方程组的过程比较复杂，我们在这里不对求解过程做过多描述，仅仅把结果展示在途中。在等式24中，u是唯一的未知量，并且我们已知u一定存在一个实数解。我们可以利用一些迭代方法（比如牛顿法）来求得一个数值解。当我们算出u，评分信息r就可以利用等式25求解出来。

总结来说，我们刚刚证明了在矩阵分解场景下，gradient会泄漏用户的信息。那么我们又该怎么解决这个问题呢？

4

联邦矩阵求解

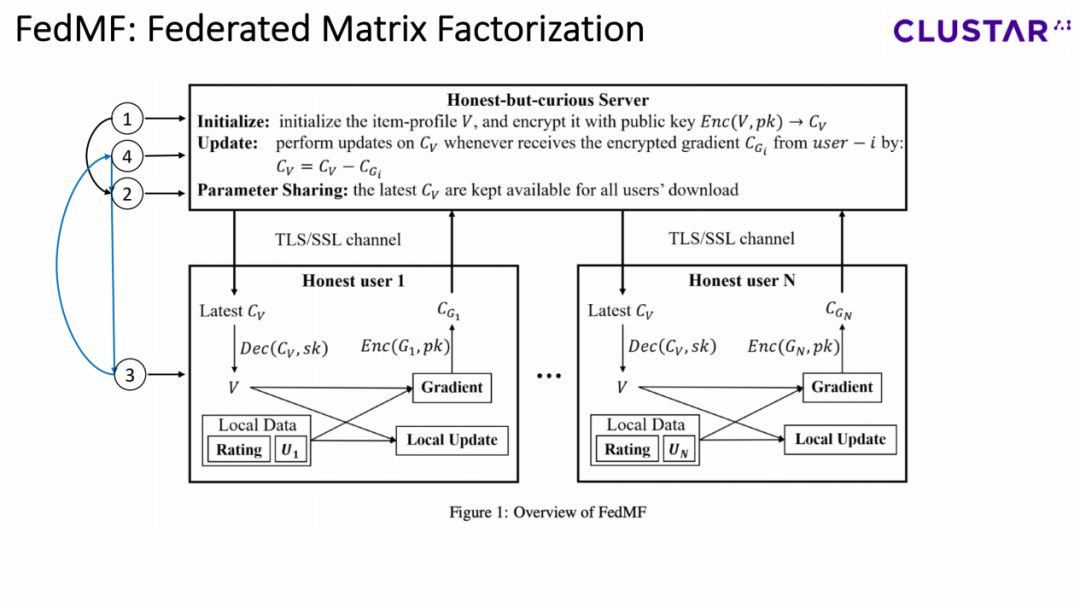
我们的解决方案是对系统中加入homomorphic encryption，也就是联邦矩阵分解系统。假设用户和服务器已经实现了对密钥的生成和分发，其中服务器拥有公钥，用户拥有彼此相同的私钥，那么整个系统就可以分为4个步骤：

第一步，对参数进行初始化，参数包括item profile矩阵和user profile矩阵，与此同时服务器对item profile使用公钥进行加密；
第二步，服务器提供加密后的item profile矩阵，供所有的用户来进行下载；

第三步，用户进行本地的update，这一步中可以拆分成若干个环节：用户首先下载加密后的item profile矩阵，并将其解密成一个plaintext V，然后用户会进行本地的update并计算gradient，最后用户会对gradient进行加密并且将ciphertext发给服务器；

接下来让我们回到整体的架构，在第四步，服务器在接收到加密后的gradient之后，会根据附加的homomorphic encryption对item profile矩阵进行更新，请注意，服务器会提供给用户最新一次加密后的item profile用作下载，此时我们就需要再一次回到第二步。

整个系统通过重复第二、三、四步，会实现整个训练过程。一般来说，用户的评价信息由一个系数矩阵组成，这也就意味着一个用户的评价其实是非常有限的。因此，两个不同的设置在我们的系统中是implemented。这两个设置会遵循系统的各个环节然而会在用户的上传环节由些许的不同。其中一种设置叫做fulltext，在这种设置中，用户会对所有的item都会上传gradient，当用户对某一个item不做出评价时，gradient为0；另外一种设置叫做parttext，用户只会将评价后的item的gradient进行上传。

这两种方式有利有弊，parttext会泄漏哪些item是用户打过分的，同时在计算效率上表现更好，而fulltext不会泄漏用户的信息，但是会需要更多的计算耗时。

实验评估结果为了测试我们设计的系统的可行性，我们使用了一个MovieLens上一个真实的电影评分数据集，这个数据集包括了100K个评分信息，由610个用户对9724个电影的打分组成。这个数据集也被用于很多其他的矩阵分解研究工作中。

在图中的参数配置下，表1显示了每次迭代过程中，使用parttext方法和fulltext方法的耗时（一次迭代，是指所有610名用户上传的gradient被用来更新一次item profile矩阵）。无论是parttext还是fulltext，当item数量不是很多时，这两种方法的耗时都比较少，同时我们可以观察到，耗时会随着item数量的增加而增长。与fulltext相比，parttext会占用更少的时间，然而parttext会泄漏一部分信息。值得一提的是，parttext会比fulltext提升了20倍的效率。

为了验证我们的系统不牺牲任何准确度，我们在一个小规模的数据集上做了一系列实验。我们采用RMSE来作为度量指标，参考图4和表2，标准矩阵分解和联邦矩阵分解的评估结果是非常相近的，区别不足0.3%。如此小的区别是由于在联邦矩阵分解中，为了简化implementation，服务器会对itemvector进行更新，仅当所有的用户都上传了他们的gradient。

在一般的矩阵分解中，服务器会更新itemvector当任何用户提供了gradient。如果这些设置都相同的话，评估结果就会完全一致。图2和3显示了随着item数量的变化，用户和服务器的更新时间的比例的变化。从图可见，约95%的时间用于了服务器的更新，这就意味着如果我们增加了服务器的算力，或者提升homomorphic encryption方法，以降低密文计算的复杂度，则计算效率会有显著提升。这就是我们下一步要做的主要工作。

5

下一步研究方向

最后，想和大家介绍一下我们未来研究工作的3个主要方向：

更加有效的homomorphic encryption。如上文提到的，约95%的时间都花在服务器update上，其中计算主要用于密文。如果我们可以提升homomorphic encryption的效率，我们的系统表现会大幅提升。

在fulltext和parttext中。实验已经显示parttext比fulltext效率更高，但是parttext会暴露用户对哪些item进行了评分。这个信息，即使没有确切的评分，可能依旧会泄漏用户敏感信息[Yang et al., 2016]。或许我们可以要求用户上传更多的gradient，而不仅仅是评分后的items，但不是全部的items，这样做可以相比较fulltext增加系统效率，同时不会泄漏评分的item。

更多安全定义。目前我们用了经典的horizontal联邦学习安全定义，这个定义架设了参与方的诚实性，以及服务器的honest-but-curious。接下来我们可以去探索更具挑战的安全定义，比如如何去建立一个安全的系统以应对honest-but-curious的服务器，同时有一些用户是恶意的，甚至有一些参与方会与server联合谋策。

点个在看 paper不断！