【统计学习方法】第3章 k近邻法（二）-技术圈

点击上方“公众号”可订阅哦！

“这个公众号在我的新作品中帮助我毫不费力地使用了解决万有引力的问题。我现在有更多时间站在树下，被苹果击中。”

Isaac Newton

实现k近邻法时，主要考虑的是如何对训练数据进行快速k近邻搜索。

下面介绍kd树方法。

kd树是对k维空间中的实例点进行储存以便对其进行快速检索的树形数据结构。kd树是二叉树，表示对k维空间的一个划分。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，构成一系列的k维超矩形区域。

●

构造平衡kd树

输入：k维空间数据集

输出：kd树

构造kd树节点

创建节点代码：

class KdNode(object):    def __init__(self, dom_elt, split, left, right):        # k维向量节点(k维空间中的一个样本点)                self.dom_elt = dom_elt          # 整数（进行分割维度的序号）        self.split = split         # 该结点分割超平面左子空间构成的kd-tree        self.left = left          # 该结点分割超平面右子空间构成的kd-tree        self.right = right

创建kd树

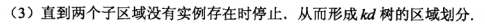
class KdTree(object):    def __init__(self, data):        k = len(data[0])  # 数据维度
        def CreateNode(split, data_set):  # 按第split维划分数据集exset创建KdNode            if not data_set:  # 数据集为空                return None            # key参数的值为一个函数，此函数只有一个参数且返回一个值用来进行比较            # operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为需要获取的数据在对象中的序号            #data_set.sort(key=itemgetter(split)) # 按要进行分割的那一维数据排序            data_set.sort(key=lambda x: x[split])            split_pos = len(data_set) // 2  # //为Python中的整数除法            median = data_set[split_pos]  # 中位数分割点            split_next = (split + 1) % k  # cycle coordinates
            # 递归的创建kd树            return KdNode(                median,                split,                CreateNode(split_next, data_set[:split_pos]),  # 创建左子树                CreateNode(split_next, data_set[split_pos + 1:]))  # 创建右子树
        self.root = CreateNode(0, data)  # 从第0维分量开始构建kd树,返回根节点

●

例题3.2

代码：

import sysimport importlibimportlib.reload(sys)
# kd-tree每个结点中主要包含的数据结构如下 class KdNode(object):    def __init__(self, dom_elt, split, left, right):        # k维向量节点(k维空间中的一个样本点)                self.dom_elt = dom_elt          # 整数（进行分割维度的序号）        self.split = split         # 该结点分割超平面左子空间构成的kd-tree        self.left = left          # 该结点分割超平面右子空间构成的kd-tree        self.right = right

class KdTree(object):    def __init__(self, data):        k = len(data[0])                 # 数据维度
        def CreateNode(split, data_set): # 按第split维划分数据集exset创建KdNode            if not data_set:                return None
            # key参数的值为一个函数，此函数只有一个参数且返回一个值用来进行比较            # operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为需要获取的数据在对象中的序号            # data_set.sort(key=itemgetter(split)) # 按要进行分割的那一维数据排序            data_set.sort(key=lambda x: x[split])            split_pos = len(data_set) // 2         # //为Python中的整数除法            median = data_set[split_pos]           # 中位数分割点                         split_next = (split + 1) % k           # cycle coordinates
            # 递归的创建kd树            return KdNode(median, split,                           CreateNode(split_next, data_set[:split_pos]),     # 创建左子树                          CreateNode(split_next, data_set[split_pos + 1:])) # 创建右子树
        self.root = CreateNode(0, data)         # 从第0维分量开始构建kd树,返回根节点
# KDTree的前序遍历def preorder(root):      print (root.dom_elt)      if root.left:      # 节点不为空        preorder(root.left)      if root.right:          preorder(root.right)

data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]kd = KdTree(data)preorder(kd.root)

输出

[7, 2][5, 4][2, 3][4, 7][9, 6][8, 1]

分割效果如图：

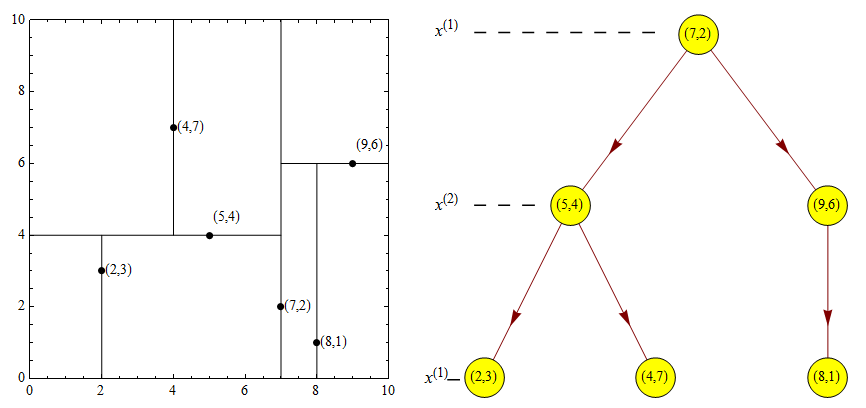
END

深度学习入门笔记

微信号:sdxx_rmbj

日常更新学习笔记、论文简述

【统计学习方法】 第3章 k近邻法（二）

【统计学习方法】第3章 k近邻法（二）