K近邻算法:以"同类相吸"解决分类问题!
前言
KNN(k-nearest neighbors)又叫做K近邻,是机器学习中相对简单好理解的算法,并且它是个几乎不需要训练就可以得到预测结果的模型。
我们常说物以类聚,人以群分,大家之所以能够成为朋友,多少是因为身上的某些特质是相近的,K近邻算法借助的就是这个思想。它使用某种方法找到样本空间中距离测试点最近的K个点,以投票表决的方式决定该测试点的标签。
本文将结合阿里云提供的机器学习算法(三): K近邻(k-nearest neighbors)初探与清华大学李航老师的PPT,来具体解释这其中的理论基础和代码实例。
1. KNN理论基础
1.1 背景介绍
大家通过视频软件挑选电影的时候,通常会先按照电影的类别进行挑选,例如动作片、爱情片、歌舞片。这些电影有各自的特点,像是动作片的打斗场景一定比爱情片多,它也不会像歌舞片一样一言不合就开始跳舞,但又不能完全排除有出现的可能。
总结这三类型的影片所具有的显著特点:打斗、亲吻、跳舞。假设现在用一个元组(a, b, c)来表示,值在0~1之间,Movie = (0.8, 0.1, 0.1)时,就认为这个电影是动作片。那么很自然的,提出了使用一个三维空间作为该数据集的样本空间,每一部电影在空间中都有属于自己的点。
假定现在把一堆电影在这个空间中表示出来,大概率会发现它们具有一定的聚集性,动作片中点与点的距离会比动作片和爱情片中点与点的距离更短。如果不能理解,也可以拿二维的做类比。
根据这个特点,提出了K近邻算法。对于给定的一个测试电影,将它在空间中标注出来,使用曼哈顿距离或者欧式距离等,选出K个距离该测试点最近的点,而我们已经事先知道了这些被选出来的最近点的电影类型,接着对其进行类型统计投票,选择票数最多的那个作为该测试电影的类型。
比如当K=5时,用a、b、c分别表示三类型电影的票数,如果a = 4, b = 1, c = 0,我们就认为这部电影是动作片。
从这个过程你可以看出,它只需要一个多维空间、带标签的训练集,因此它也是个有监督学习。
1.2 工作原理与特点
K近邻算法的工作原理如下:
首先,存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每个数据与所属分类的对应关系。
其次,输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。一般来说,只选择样本数据集中前N个最相似的数据。K一般不大于20。
最后,选择k个中出现次数最多的分类,作为新数据的分类。
借个《机器学习实战》中的例子,下图是每部电影的打斗镜头数、接吻镜头数以及电影评估类型,其中有一部未知电影的接吻镜头有90次,打斗18次,电影类型是未知的。
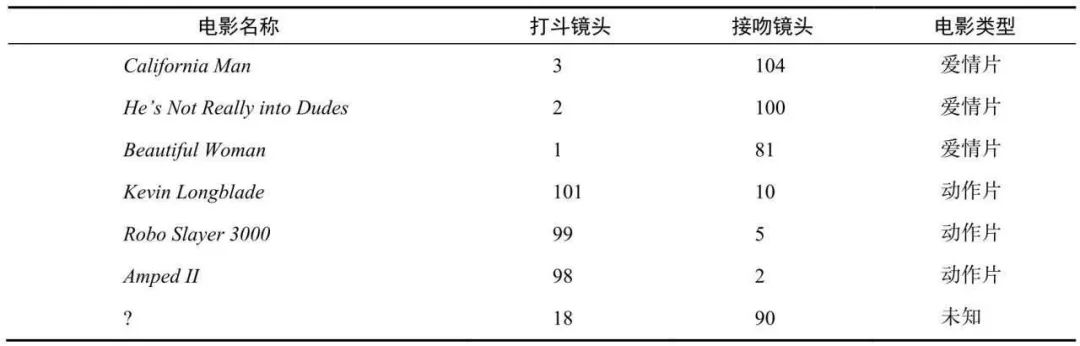 那么接下来通过计算未知电影与样本集合中其他电影的距离:
那么接下来通过计算未知电影与样本集合中其他电影的距离: 现在我们得到了样本集中所有电影与未知电影的距离,按照距离递增排序,可以找到k个距离最近的电影。假定k=3,则三个最靠近的电影依次是He's Not Really into Dudes、Beautiful Woman和California Man。k-近邻算法按照距离最近的三部电影的类型,决定未知电影的类型,而这三部电影全是爱情片,因此我们判定未知电影是爱情片。
现在我们得到了样本集中所有电影与未知电影的距离,按照距离递增排序,可以找到k个距离最近的电影。假定k=3,则三个最靠近的电影依次是He's Not Really into Dudes、Beautiful Woman和California Man。k-近邻算法按照距离最近的三部电影的类型,决定未知电影的类型,而这三部电影全是爱情片,因此我们判定未知电影是爱情片。K近邻算法的特点也显而易见,由于选择了K个邻近的参考点,因此它的精度较高,且对异常值不敏感,无数据输入假定,使用于数值型和标称型的数据。缺点是计算复杂度和空间复杂度双高。
1.3 处理流程
收集数据:可以使用任何方法。 准备数据:距离计算所需要的数值,最好是结构化的数据格式。 分析数据:可以使用任何方法。 训练算法:此步骤不适用于k-近邻算法。 测试算法:计算错误率。 使用算法:首先需要输入样本数据和结构化的输出结果,然后运行k近邻算法判定输入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理。
1.4 距离计算
如果你认真的看到这里,比较迷惑的点大概就在于距离应该如何计算度量。
样本之间的距离的计算,我们一般使用对于一般使用Lp距离进行计算。
当p=1时候,称为曼哈顿距离(Manhattan distance)。
当p=2时候,称为欧氏距离(Euclidean distance)。
当p=∞时候,称为极大距离(infty distance),表示各个坐标的距离最大值,另外也包含夹角余弦等方法。
一般采用欧式距离较多,但是文本分类则倾向于使用余弦来计算相似度。
对于两个向量,一般使用距离进行计算。假设特征空间是n维实数向量空间 , 其中,, , 的距离定义为:
这里的. 当时候,称为欧氏距离(Euclidean distance):
当时候,称为曼哈顿距离(Manhattan distance):
当时候,称为极大距离(infty distance), 表示各个坐标的距离最大值:
需要注意的一点是,对于那些存在缺失值的数据,应该如何使用欧式距离进行计算呢?
接下来我们来详细举例说明:
正常的欧式距离:每个维度上都有数值。
带有空值的欧式聚类:某个或多个维度上的值为空NaN。
只计算所有非空的值,对所有空加权到非空值的计算上,上例中,我们看到一个有3维,只有第二维全部非空,将第一维和第三维的计算加到第二维上,所有需要乘以3。
当然这个空值我们也是需要处理一下的,需要计算每个样本最近的k个样本,使用简单的加权平均进行填充。
比如当k=2时,样本[1, 2, np.nan] 最近的2个样本是: [3, 4, 3] [np.nan, 6, 5], 计算距离的时候使用欧式距离,只关注非空样本。[1, 2, np.nan] 填充之后得到 [1, 2, (3 + 5) / 2] = [1, 2, 4]。
| 带有空值的样本 | 最相近的样本1 | 最相近的样本2 | 填充之后的值 |
|---|---|---|---|
| [1, 2, np.nan] | [3, 4, 3]; 3.46 | [np.nan, 6, 5]; 6.93 | [1, 2, 4] |
| [np.nan, 6, 5] | [3, 4, 3]; 3.46 | [8, 8, 7]; 3.46 | [5.5, 6, 5] |
所以,这样我们碰到缺失值就再也不用害怕啦!
1.5 K值选择
另外一个困惑就是K值的选择。
如果选择较小的K值,“学习”的近似误差(approximation error)会减小,但 “学习”的估计误差(estimation error) 会增大,噪声敏感,K值的减小就意味着整体模型变得复杂,容易发生过拟合。
如当K=1时,预测的结果只和最近的一个训练样本相关,此时很容易发生过拟合。
如果选择较大的K值,可以减少学习的估计误差,但缺点是学习的近似误差会增大。K值的增大就意味着整体的模型变得简单。
如当K=20时,预测的结果和最近的20个样本相关,假如我们只有20个样本,此时是所有样本的平均值,此时所有预测值都是均值,很容易发生欠拟合。
一般情况下,使用KNN的时候,根据数据规模我们会从[3, 20]之间进行尝试,选择最好的K。
2. 代码实践
我们借助鸢尾花的案例案例,了解在无缺失数值的数据集中,如何实现KNN算法。再借助马绞痛数据来练习数据预处理,以及KNN分类的pipeline。
2.1 鸢尾花案例
第一步,首先库函数导入:
import numpy as np
import matplotlib.pyplot as plt
# 导入KNN分类器
from sklearn.neighbors import KNeighborsClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
第二步,载入鸢尾花的数据集,并按照8:2的比例划分训练集与测试集:
# 载入鸢尾花数据集
# iris是一个对象类型的数据,其中包括了data(鸢尾花的特征)和target(也就是分类标签)
iris = datasets.load_iris()
# 将样本与标签分开
x = iris['data']
y = iris['target']
print(x.shape, y.shape) # (150, 4) (150,)
# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2) # 8:2
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
# (120, 4) (30, 4) (120,) (30,)
第三步,使用KNeighborsClassifier来训练模型,这里我们设置参数k(n_neighbors)=5, 使用欧式距离(metric=minkowski & p=2):
clf = KNeighborsClassifier(n_neighbors=5, p=2, metric="minkowski")
clf.fit(x_train, y_train) # fit可以简单的认为是表格存储
# KNeighborsClassifier()
第四步,使用predict函数进行模型预测,并计算出预测准确率:
y_predict = clf.predict(x_test)
y_predict.shape # (30,)
acc = sum(y_predict == y_test) / y_test.shape[0]
acc
得到最终的准确率为0.933。
2.2 马绞痛案例
马可能会发生一些病变,该数据集可以这么下载:
# 下载需要用到的数据集
!wget https://tianchi-media.oss-cn-beijing.aliyuncs.com/DSW/3K/horse-colic.csv
第一步,首先库函数导入:
import numpy as np
import pandas as pd
# kNN分类器
from sklearn.neighbors import KNeighborsClassifier
# kNN数据空值填充
from sklearn.impute import KNNImputer
# 计算带有空值的欧式距离
from sklearn.metrics.pairwise import nan_euclidean_distances
# 交叉验证
from sklearn.model_selection import cross_val_score
# KFlod的函数
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
第二步,读出csv文件,并且简要观察其数据特点:
temp = pd.read_csv('KNN.csv', header=None)
temp # 数据的第23列表示是否病变,1为yes,2为no
明显发现数据有些小'?',比如第一行的第8列和第20、21列。
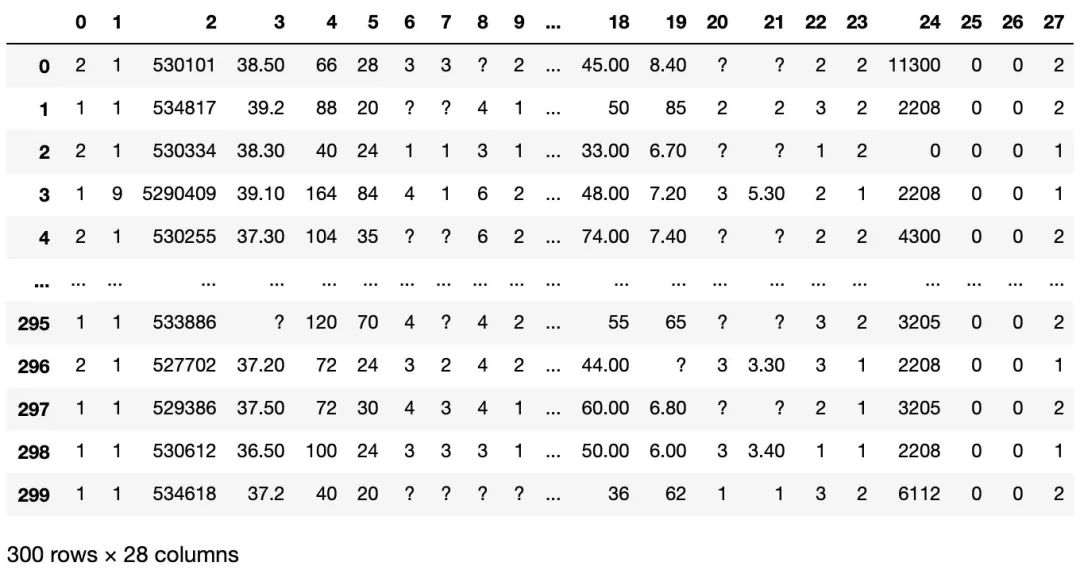
所以我们应该在读取的时候就把这些问号改成NaN,以便之后的处理:
df = pd.read_csv('KNN.csv', header=None, na_values='?') # na_values='?'
df
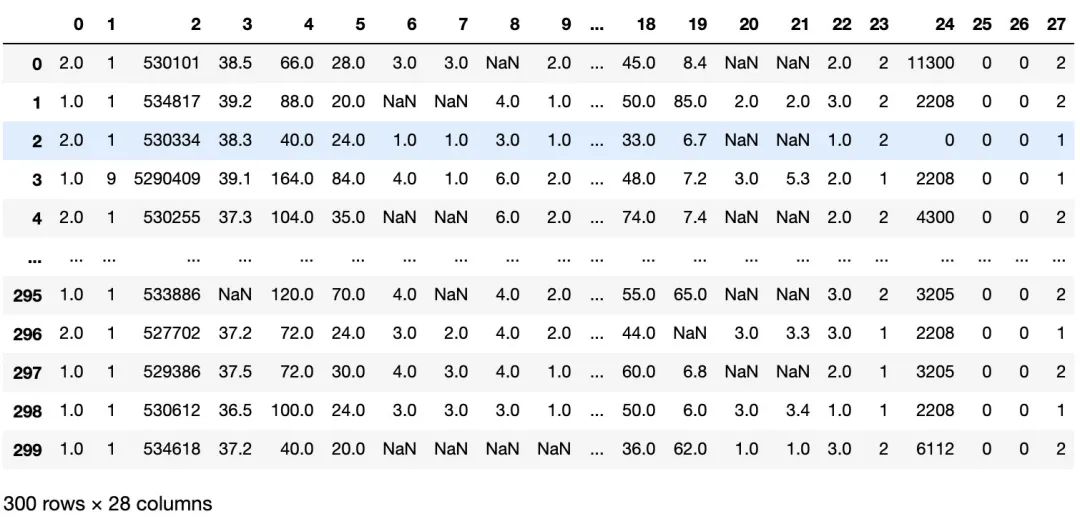
现在我们知道,该原始数据有300行,28列,并且存在NaN值待处理,其中数据的第23列表示是否病变,1为yes,2为no。
第三步,单独提取出了病变结果列,并统计每一列的数据缺失个数:
data = df.values # 原始数据有300行,28列
x_index = [i for i in range(data.shape[1]) if i != 23]
x, y = data[:, x_index], data[:, 23] # 单独提取出了病变结果列
print(x.shape, y.shape) # (300, 27) (300,)
cols_null=[]
for i in range(x.shape[1]):
cols_null.append(df[i].isnull().sum()) # 每一列的数据缺失个数
cols_null # [1, 0, 0,60, 24, 58, ...]
第四步,处理空值,进行数值填充。这里我们使用KNNImputer进行空值填充,其填充方法和之前在距离计算那里提到的计算方式是一样的,所以就不再赘述:
imputer = KNNImputer()
# 填充数据集中的空值
x1 = imputer.fit_transform(x) # 或者是fit和transform分开写
print(sum(np.isnan(x1))) # 处理后不再存在空值
print(sum(np.isnan(x)))
# [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
# [ 1 0 0 60 24 58 56 69 47 32 55 44 56 104 106 247 102 118 29 33 165 198 1 0 0 0 0]
接着你可以使用KNeighborsClassifier来处理该数据,详细参考鸢尾花案例。
这里我们再介绍一种数据管道Pipeline的方式,任何有序的操作有可以看做pipeline,例如工厂流水线,对于机器学习模型来说,也就是数据流水线。是指数据通过管道中的每一个节点,结果除了之后,继续流向下游。
对于我们这个例子,数据是有空值,我们会有一个KNNImputer节点用来填充空值,之后继续流向下一个kNN分类节点,最后输出模型。

所以将第四和第五步结合,使用数据管道来处理:
# 使用数据管道来处理
pipe = Pipeline(steps=[('imputer', KNNImputer(n_neighbors=5)), ('model', c())])
# 得到训练集合和验证集合, 8: 2
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
# 验证model
pipe.fit(x_train, y_train)
score = pipe.score(x_test, y_test)
score # 0.8166
最终得到分数为0.817,其实结果并不是很高,可能和K值的设定有关,具体设置为多少效果会更好,就留给你自己去探究。
参考资料
《机器学习实战》 https://developer.aliyun.com/ai/scenario/febc2223e46f419dae84df47b1760ffc
