【机器学习】梯度下降的Python实现

作者 | Vagif Aliyev 

编译 | VK 

来源 | Towards Data Science

梯度下降是数据科学的基础，无论是深度学习还是机器学习。对梯度下降原理的深入了解一定会对你今后的工作有所帮助。

你将真正了解这些超参数的作用、在背后发生的情况以及如何处理使用此算法可能遇到的问题，而不是玩弄超参数并希望获得最佳结果。

然而，梯度下降并不局限于一种算法。另外两种流行的梯度下降（随机和小批量梯度下降）建立在主要算法的基础上，你可能会看到比普通批量梯度下降更多的算法。因此，我们也必须对这些算法有一个坚实的了解，因为它们有一些额外的超参数，当我们的算法没有达到我们期望的性能时，我们需要理解和分析这些超参数。

虽然理论对于深入理解手头的算法至关重要，但梯度下降的实际编码及其不同的“变体”可能是一项困难的任务。为了完成这项任务，本文的格式如下：

1. 简要概述每种算法的作用。

2. 算法的代码

3. 对规范不明确部分的进一步解释

我们将使用著名的波士顿住房数据集，它是预先内置在scikit learn中的。我们还将从头开始构建一个线性模型

好的，首先让我们做一些基本的导入。我不打算在这里做EDA，因为这不是我们文章的真正目的。不过，我会把一些事情说明白。

import numpy as np
import pandas as pd 
import plotly.express as px
from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error

好的，为了让我们看到数据是什么样子，我将把数据转换成一个数据帧并显示输出。

data = load_boston()

df = pd.DataFrame(data['data'],columns=data['feature_names'])
df.insert(13,'target',data['target'])
df.head(5)

好吧，这里没什么特别的，我敢肯定你之前已经类似实现过了。

现在，我们将定义我们的特征（X）和目标（y）。我们还将定义我们的参数向量，将其命名为thetas，并将它们初始化为零。

X,y = df.drop('target',axis=1),df['target']

thetas = np.zeros(X.shape[1])

成本函数

回想一下，成本函数是衡量模型性能的东西，也是梯度下降的目标。我们将使用的代价函数称为均方误差。公式如下：

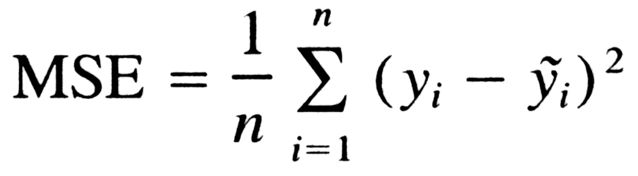
好吧，我们把它写出来：

def cost_function(X,Y,B):
    predictions = np.dot(X,B.T)
    
    cost = (1/len(Y)) * np.sum((predictions - Y) ** 2)
    return cost

在这里，我们将输入、标签和参数作为输入，并使用线性模型进行预测，得到成本，然后返回。如果第二行让你困惑，回想一下线性回归公式：

所以，我们基本上是得到每个特征和它们相应权重之间的点积。如果你还不确定我在说什么，看看这个视频：https://www.youtube.com/watch?v=kHwlB_j7Hkc

很好，现在让我们测试一下我们的成本函数，看看它是否真的有效。为了做到这一点，我们将使用scikit learn的均方误差，得到结果，并将其与我们的算法进行比较。

mean_squared_error(np.dot(X,thetas.T),y)

OUT: 592.14691169960474

cost_function(X,y,thetas)

OUT: 592.14691169960474

太棒了，我们的成本函数起作用了！

特征缩放

特征缩放是线性模型（线性回归、KNN、SVM）的重要预处理技术。本质上，特征被缩小到更小的范围，并且特征也在一定的范围内。可以这样考虑特征缩放：

1. 你有一座很大的建筑物

2. 你希望保持建筑的形状，但希望将其调整为较小的比例

特征缩放通常用于以下场景：

1. 如果一个算法使用欧几里德距离，那么由于欧几里德距离对较大的量值敏感，因此需要对特征进行缩放

2. 特征缩放还可以用于数据标准化

3. 特征缩放还可以提高算法的速度

虽然有许多不同的特征缩放方法，但我们将使用以下公式构建MinMaxScaler的自定义实现：

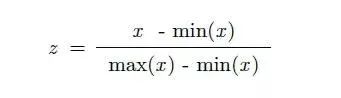
由于上述原因，我们将使用缩放。

现在，对于python实现：

X_norm = (X - X.min()) / (X.max() - X.min())
X = X_norm

这里没什么特别的，我们只是把公式翻译成代码。现在，节目真正开始了：梯度下降！

梯度下降

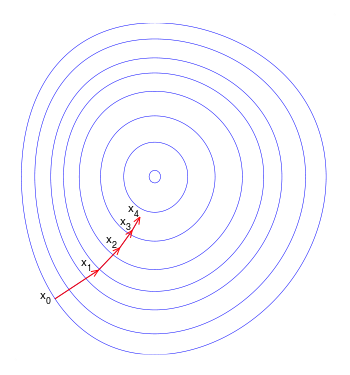
具体地说，梯度下降是一种优化算法，它通过迭代遍历数据并获得偏导数来寻求函数的最小值（在我们的例子中是MSE）。

如果这有点复杂，试着把梯度下降想象成是一个人站在山顶上，他们试着以最快的速度从山上爬下来，沿着山的负方向不断地“走”，直到到达底部。

现在，梯度下降有不同的版本，但是你会遇到最多的是：

1. 批量梯度下降

2. 随机梯度下降法

3. 小批量梯度下降

现在我们将按顺序讨论、实现和分析每一项，所以让我们开始吧！

批量梯度下降

批量梯度下降可能是你遇到的第一种梯度下降类型。现在，我在这篇文章中并不是很理论化（你可以参考我以前的文章：https://medium.com/@vagifaliyev/gradient-descent-clearly-explained-in-python-part-1-the-troubling-theory-49a7fa2c4c06），但实际上它计算的是整个（批处理）数据集上系数的偏导数。你可能已经猜到这样做很慢了。

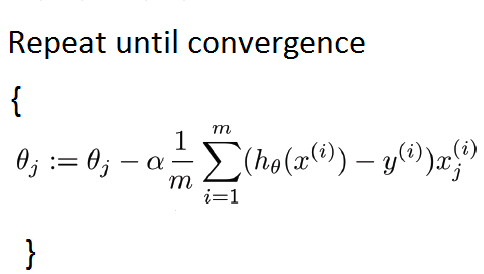
我们的数据集很小，所以我们可以像这样实现批量梯度下降：

def batch_gradient_descent(X,Y,theta,alpha,iters):
    cost_history = [0] * iters  # 初始化历史损失列表
    for i in range(iters):         
        prediction = np.dot(X,theta.T)                  
        theta = theta - (alpha/len(Y)) * np.dot(prediction - Y,X)   
        cost_history[i] = cost_function(X,Y,theta)               
    return theta,cost_history

要澄清一些术语：

alpha：这是指学习率。

iters：迭代运行的数量。

太好了，现在让我们看看结果吧！

batch_theta,batch_history=batch_gradient_descent(X,y,theta,0.05,500)

好吧，不是很快，但也不是很慢。让我们用我们新的和改进的参数来可视化和成本：

cost_function(X,y,batch_theta)

OUT: 27.537447130784262

哇，从592到27！这只是一个梯度下降的力量的一瞥！让我们对迭代次数的成本函数进行可视化：

fig = px.line(batch_history,x=range(5000),y=batch_history,labels={'x':'no. of iterations','y':'cost function'})
fig.show()

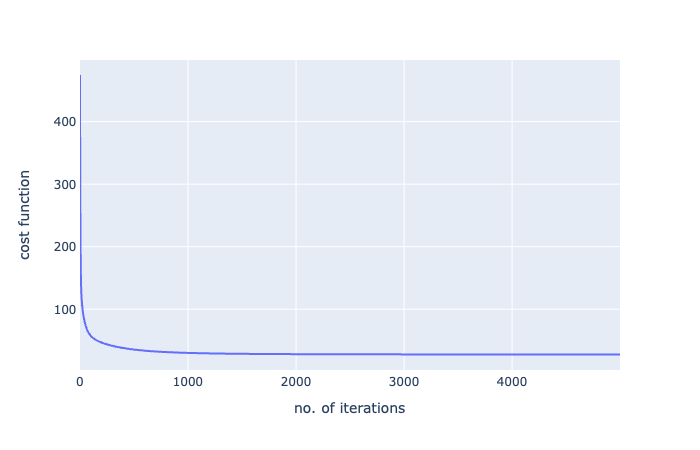
好的，看看这个图表，我们在大约100次迭代之后达到了一个大的下降，从那里开始，它一直在逐渐减少。

所以，批量梯度下降到此结束：

优点

1. 有效且曲线平滑

2. 最准确，最有可能达到全局最低值

缺点

1. 对于大型数据集可能会很慢

2. 计算成本高

随机梯度下降法

这里，不是计算整个训练集的偏导数，而是只计算一个随机样本（随机意义上的随机）。

这是很好的，因为计算只需要在一个训练示例上进行，而不是在整个训练集上进行，这使得计算速度更快，而且对于大型数据集来说非常理想。

然而，由于其随机性，随机梯度下降并不像批量梯度下降那样具有平滑的曲线，虽然它可以返回良好的参数，但不能保证达到全局最小值。

学习率调整

解决随机梯度下降问题的一种方法是学习率调整。

基本上，这会逐渐降低学习率。因此，学习率一开始很大（这有助于避免局部极小值），当学习率接近全局最小值时，学习率逐渐降低。但是，你必须小心：

1. 如果学习速率降低得太快，那么算法可能会陷入局部极小，或者在达到最小值的一半时停滞不前。

2. 如果学习速率降低太慢，可能会在很长一段时间内跳转到最小值附近，仍然无法得到最佳参数

现在，我们将使用简易的学习率调整策略实现随机梯度下降：

t0,t1 = 5,50 # 学习率超参数

def learning_schedule(t):
    return t0/(t+t1)
    
def stochastic_gradient_descent(X,y,thetas,n_epochs=30):
    c_hist = [0] * n_epochs # 历史成本
    for epoch in range(n_epochs):
        for i in range(len(y)):
            random_index = np.random.randint(len(Y))
            xi = X[random_index:random_index+1]
            yi = y[random_index:random_index+1]
            
            prediction = xi.dot(thetas)
            
            gradient = 2 * xi.T.dot(prediction-yi)
            eta = learning_schedule(epoch * len(Y) + i)
            thetas = thetas - eta * gradient
            c_hist[epoch] = cost_function(xi,yi,thetas)
    return thetas,c_hist

现在运行函数：

sdg_thetas,sgd_cost_hist = stochastic_gradient_descent(X,Y,theta)

好吧，太好了，这样就行了！现在让我们看看结果：

cost_function(X,y,sdg_thetas)

OUT:
29.833230764634493

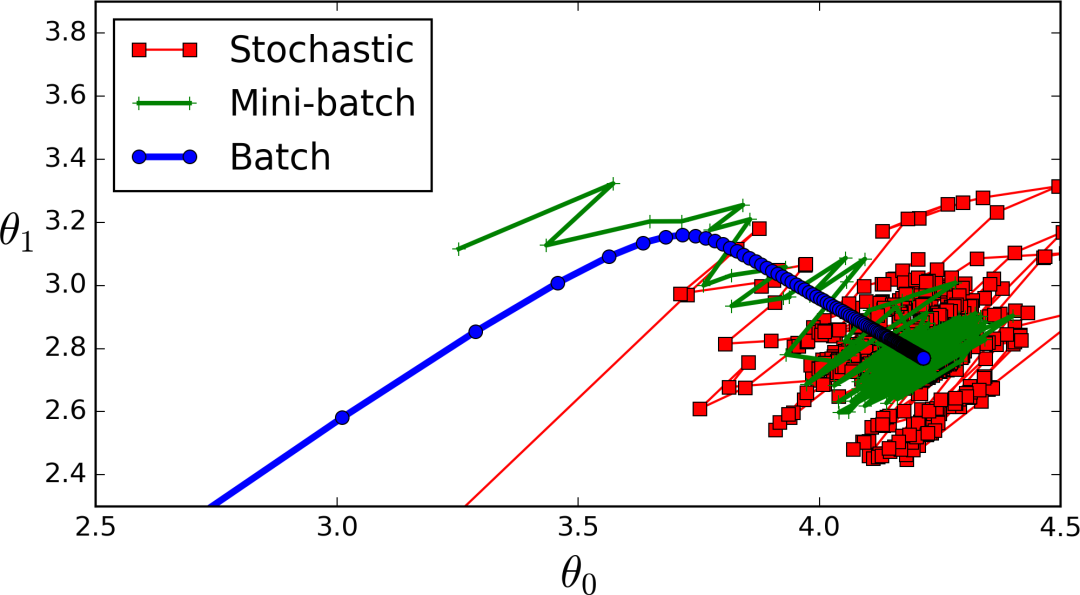
哇！我们从592到29，但是请注意：我们只进行了30次迭代。批量梯度下降，500次迭代后得到27次！这只是对随机梯度下降的非凡力量的一瞥。

让我们用一个图再次将其可视化：

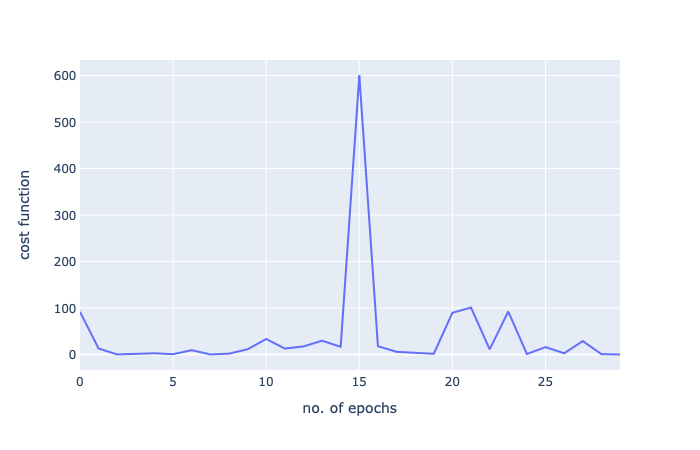
由于这是一个小数据集，批量梯度下降就足够了，但这只是显示了随机梯度下降的力量。

优点：

1. 与批量梯度下降相比更快

2. 更好地处理更大的数据集

缺点：

1. 在某个最小值上很难跳出

2. 并不总是有一个清晰的图，可以在一个最小值附近反弹，但永远不会达到最佳的最小值

小批量梯度下降

好了，快到了，还有一个要通过！现在，在小批量梯度下降中，我们不再计算整个训练集或随机样本的偏导数，而是在整个训练集的小子集上计算。

这给了我们比批量梯度下降更快的速度，因为它不像随机梯度下降那样随机，所以我们更接近于最小值。然而，它很容易陷入局部极小值。

同样，为了解决陷入局部最小值的问题，我们将在实现中使用简易的学习率调整。

np.random.seed(42) # 所以我们得到相同的结果

t0, t1 = 200, 1000
def learning_schedule(t):
    return t0 / (t + t1)
    
def mini_batch_gradient_descent(X,y,thetas,n_iters=100,batch_size=20):
    t = 0
    c_hist = [0] * n_iters
    for epoch in range(n_iters):
        shuffled_indices = np.random.permutation(len(y))
        X_shuffled = X_scaled[shuffled_indices]
        y_shuffled = y[shuffled_indices]
        
        for i in range(0,len(Y),batch_size):
            t+=1
            xi = X_shuffled[i:i+batch_size]
            yi = y_shuffled[i:i+batch_size]
            
            gradient = 2/batch_size * xi.T.dot(xi.dot(thetas) - yi)
            eta = learning_schedule(t)
            thetas = thetas - eta * gradient
            c_hist[epoch] = cost_function(xi,yi,thetas)
    return thetas,c_hist

让我们运行并获得结果：

mini_batch_gd_thetas,mini_batch_gd_cost = mini_batch_gradient_descent(X,y,theta)

以及新参数下的成本函数：

cost_function(X,Y,mini_batch_gd_thetas)

OUT: 27.509689139167012

又一次真的很棒。我们运行了1/5的迭代，我们得到了一个更好的分数！

让我们再画出函数：

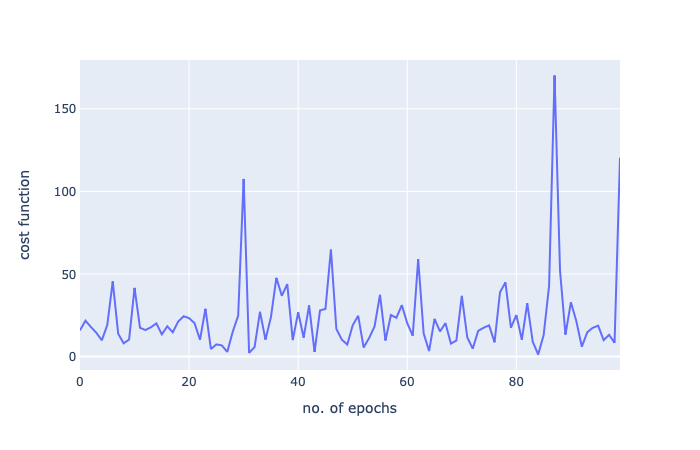
好了，我的梯度下降系列到此结束！感谢阅读！