蒙特卡洛与赌博模型
日期:2020年08月05日
正文共:1755字13图
预计阅读时间:5分钟
来源:Toby
来,先谈一部电影!
《决胜21点》讲述了几位数学天才少年凭才智大闹赌城拉斯维加斯的故事。举世闻名的麻省理工,堪称是莘莘学子、科学天才们向往的圣地。作为有幸能到这里读书的新生,本·坎贝尔(吉姆·斯特吉斯饰)自然也有他的过人之处。的确,坎贝尔超常的数学运算才能在他进入麻省理工没多久就开始崭露头角。学院里讲授数学理论课程的米基·罗萨(凯文·史派西饰)更是一眼就看中了小伙子,并对其光明的未来充满了信心。经过短暂的接触之后,罗萨教授将这位数学天才介绍给他精心培养的另外几位数学高才生认识,并邀其加入一个由罗萨领导,由吉尔(凯特·波茨沃斯饰)、费舍(雅各布·皮特斯饰)等数学天才共同组成的“特殊团队”,专攻赌场上风行的“21点”游戏。运用他们对于数学的尖端认识和运算,在经验丰富的罗萨教授的指导下,轻松应对“21点”游戏中可能出现的各种局面,最终确保高频率地取胜纪录。
诶?听上去貌似都有点道理!您觉得呢?手指继续动,跟我继续看下去……
下面我开始数学建模,然后用蒙特卡洛模拟历史上最常见的几种赌博模型。

■ ■ ■
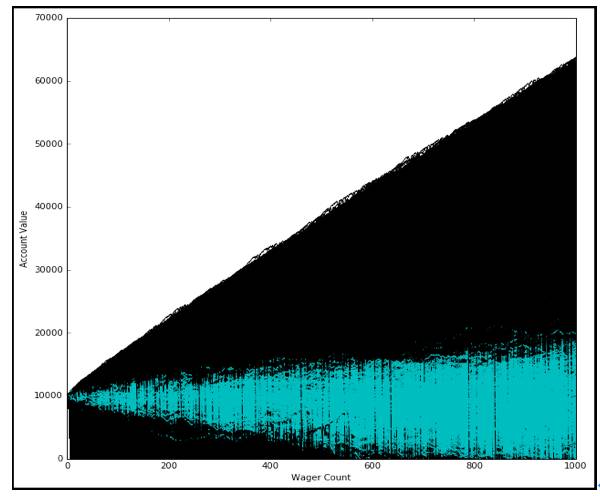
symplebedding system
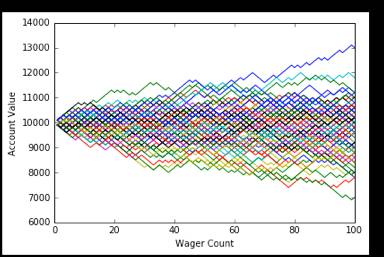
simple_bettor(10000,100,1000)
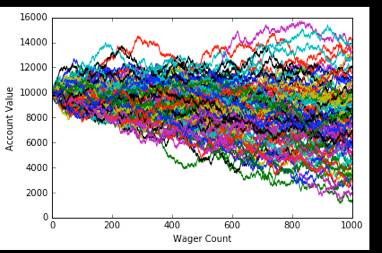
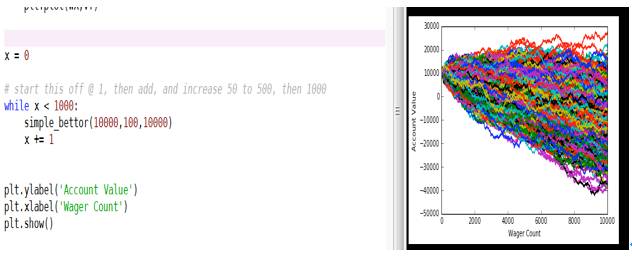
■ ■ ■

■ ■ ■

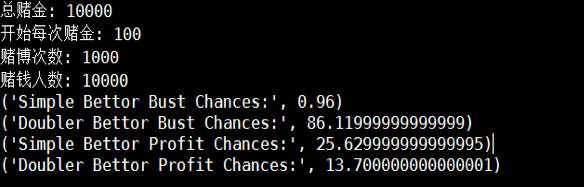
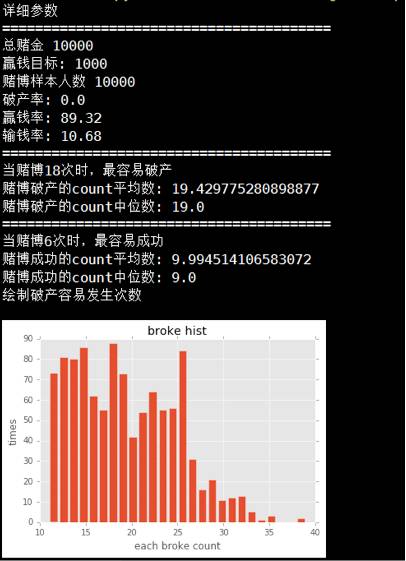
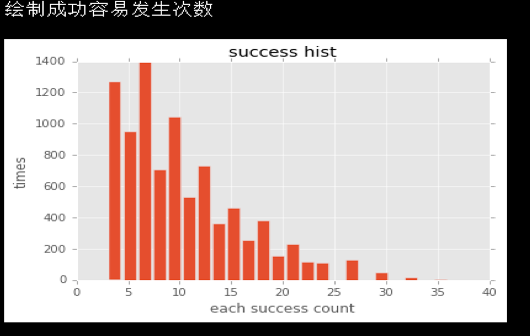
优点:破产率几乎为0
缺点:赢钱率不高,64%左右,赢的钱不多,做多10%左右
■ ■ ■

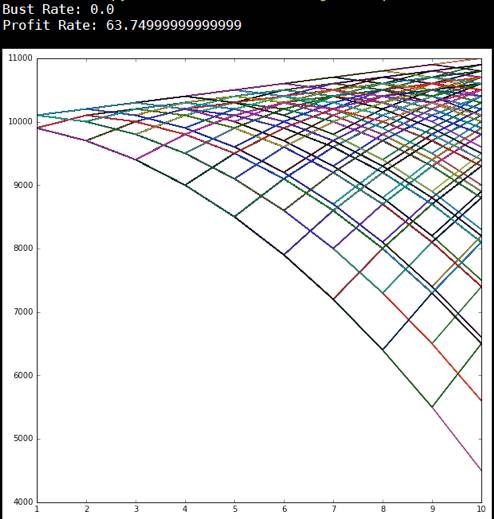
1.目标明确,减少多余风险
2.吸收 D'Alembert算法优点,减少倍数带来巨大波动风险
3.分治算法,把目标分成几等分,逐步实现
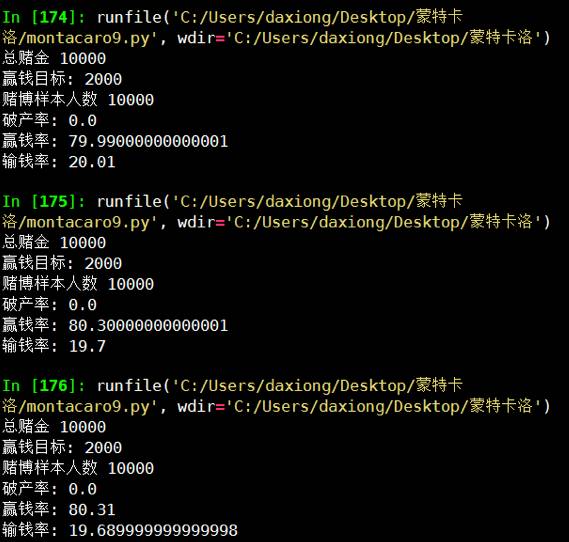
4.总赌金和目标比值10:1合理,能有足够赌金和时间空间去赢钱或达到目的
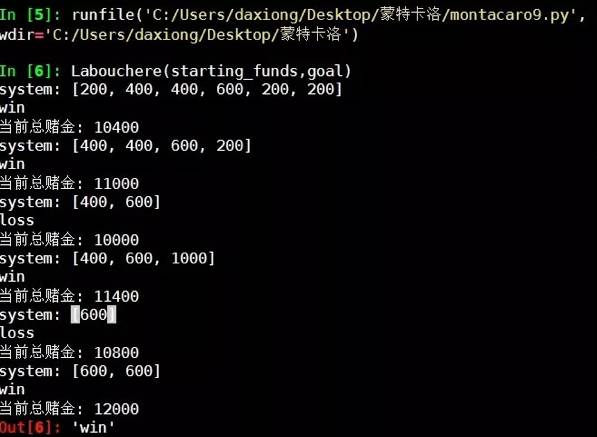
总赌金和赢取目标金额比例是1/10,胜率就有百分之90

— THE END —

评论
