(附代码)YOLOv4损失函数全面解析
如果您对YOLO V4的结构比较感兴趣,建议您可以结合代码以及我的这篇文章进行消化。代码是基于Keras版本的,结构很清晰,链接如下:
YOLO V4 Keras:https:github.com/Ma-Dan/keras-yolo4
YOLO V4原文中提到,在进行bounding box regression的时候,传统的目标检测模型(比如YOLO V3)等,都是直接根据预测框和真实框的中心点坐标以及宽高信息设定MSE(均方误差)损失函数的。为了方便大家理解,下面给出了YOLO V3的总损失函数。
可以看出,第一行的两个,就是用在bounding box regression的损失函数MSE。有关该损失函数的具体解析可以见我文章《YOLO V3 深度解析 (下)》(https://zhuanlan.zhihu.com/p/138857662),这里就不进行赘述。
鉴于MSE存在的一些问题,比如原文中提到
However, to directly estimate the coordinate values of each point of the BBox is to treat these points as independent variables, but in fact does not consider the integrity of the object itself.
意思就是MSE损失函数将检测框中心点坐标和宽高等信息作为独立的变量对待的,但是实际上他们之间是有关系的。从直观上来说,框的中心点和宽高的确存在着一定的关系。所以解决方法是使用IOU损失代替MSE损失。
接着作者就IOU损失依次提到了以下的一些的损失函数。
(1)IOU损失 (2)GIOU损失 (3)DIOU损失 (4)CIOU损失
(1)IOU损失
其中IOU损失定义非常简单,即1与预测框A和真实框B之间交并比的差值
但是这样该损失函数会有一些问题,该损失函数只在bounding box重叠的时候才管用,在他们没有重叠情况下,将不会提供滑动梯度。(这句话摘自论文《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》)
(2)GIOU损失
其实GIOU的全称叫做 :generalized IoU loss。提出来是为了缓解上述IOU损失在检测框不重叠时出现的梯度问题。定义也是比较简单的,就在在原来的IOU损失的基础上加上一个惩罚项,公式如下:
上式中A是预测框,B是真实框,C是A和B的最小包围框,A,B,C的关系具体如下图所示。
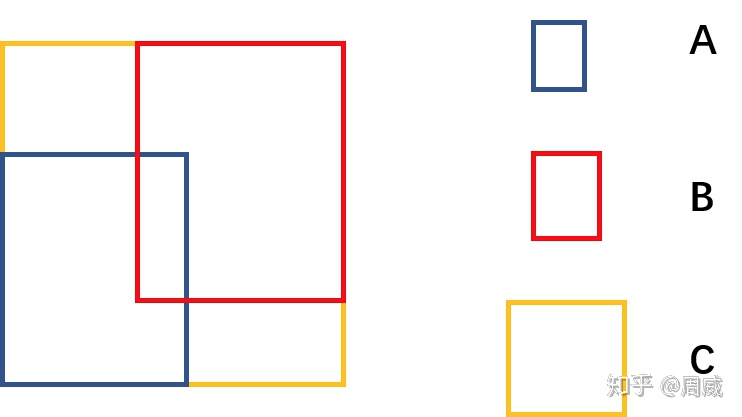
A,B,C含义
那么该惩罚项的意思就是下图右边黄色区域的比值。
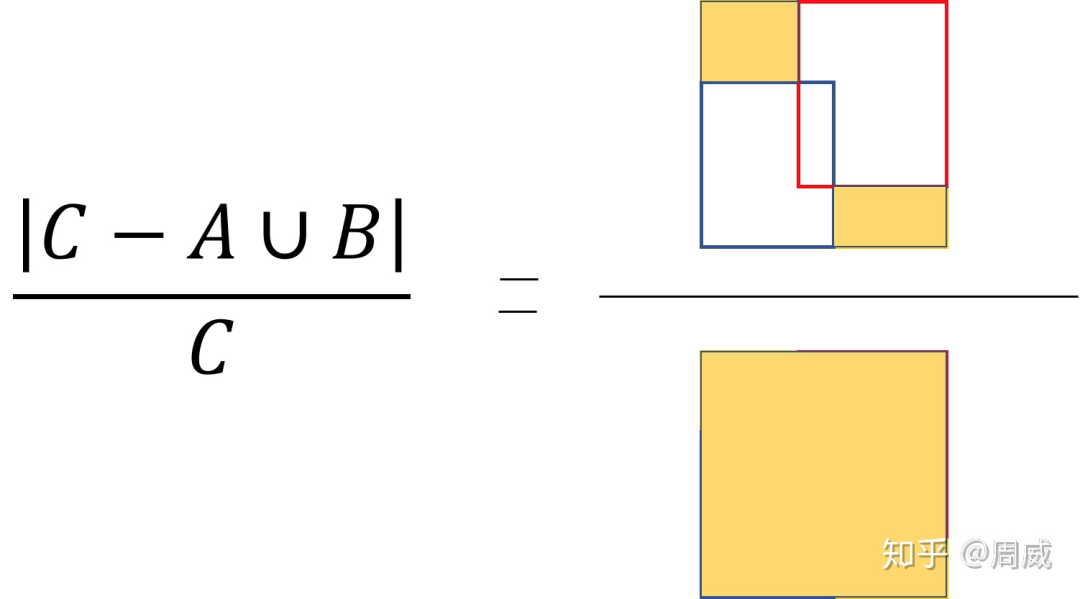
惩罚项含义
虽然GIOU可以解决检测框非重叠造成的梯度消失问题,但是他还存在以下的限制,这里我们依旧是参考CIOU论文中的内容。
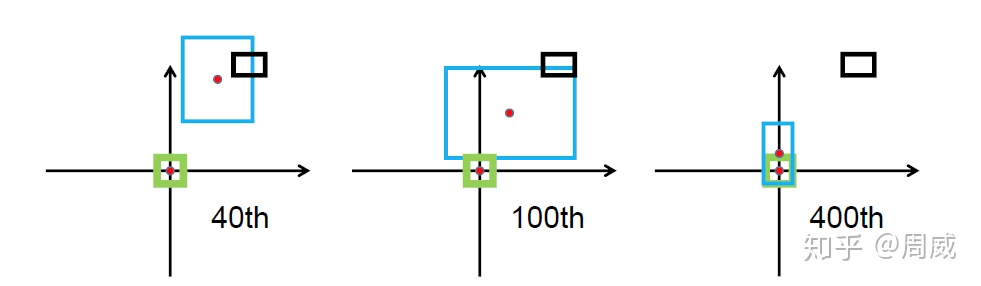
GIOU回归过程
上图中绿色为真实框,黑色为先验框Anchor,蓝色为预测框。预测框是以先验框为基础进行位置移动和大小缩放的。可以看出来,GIOU首先尝试增大预测框的大小,使得它能够与真实框有所重叠(如上图中间所示),然后才能进行上述公式中 的计算。那么这样做的话,会消耗大量的时间在预测框尝试与真实框接触上,这会影响损失的收敛速度。所以DIOU和GIOU的提出解决了上述GIOU的问题。
(3)DIOU
DIOU和CIOU都出自论文《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》(https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1911.08287)。作者说他直接在IOU损失的基础上加了一个简单的惩罚项,用来最小化两个检测框中心点的标准化距离, 这样可以加速损失的收敛过程。如下图所示为GIOU和DIOU的对比。

红色框是DIOU损失中的预测框。可以很明显的看出,DIOU的收敛速度较GIOU更快。
那么有关DIOU的定义是怎么样的呢?下面给出公式定义:
相比于IOU损失,DIOU损失也多出了一个惩罚项 。该惩罚项具体的参数含义为
A : 预测框 B:真实框 : 预测框中心点坐标 :真实框中心点坐标 是欧式距离的计算 c 为 A , B 最小包围框的对角线长度
我给出了下图,便于大家理解。
所以两个框距离越远,DIOU越接近2,距离越近,DIOU越接近0。
提出DIOU还不够,作者进一步地提出了CIOU(Complete IoU Loss)。
(4)CIOU
CIOU作者考虑的更加全面一些,DIOU考虑到了两个检测框的中心距离。而CIOU考虑到了三个几何因素,分别为
(1)重叠面积 (2)中心点距离 (3)长宽比
这里仔细观察,会发现,CIOU比DIOU多了一个长宽比的信息,那么CIOU的公式定义如下:
那么这个 对长宽比的惩罚项了。论文中提到, 是一个正数, 用来测量长宽比的一致性(v measures the consistency of aspect ratio)。具体定义如下:

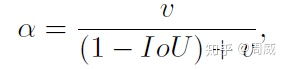
上述公式中,参数说明如下:
和 为真实框的宽、高 和 为预测框的宽、高
若真实框和预测框的宽高相似,那么 为0,该惩罚项就不起作用了。所以很直观地,这个惩罚项作用就是控制预测框的宽高能够尽可能快速地与真实框的宽高接近。
那么至此,有关YOLO V4损失函数的理论部分就说完了。
3.IOU损失函数的实战部分
说完了上述四个IOU理论部分,我们回归其在YOLO V4框架中的位置并进行解析。结合keras的代码,如下为CIOU损失函数的定义。
def bbox_ciou(boxes1, boxes2):'''计算ciou = iou - p2/c2 - av:param boxes1: (8, 13, 13, 3, 4) pred_xywh:param boxes2: (8, 13, 13, 3, 4) label_xywh:return:
举例时假设pred_xywh和label_xywh的shape都是(1, 4)'''
# 变成左上角坐标、右下角坐标boxes1_x0y0x1y1 = tf.concat([boxes1[..., :2] - boxes1[..., 2:] * 0.5,boxes1[..., :2] + boxes1[..., 2:] * 0.5], axis=-1)boxes2_x0y0x1y1 = tf.concat([boxes2[..., :2] - boxes2[..., 2:] * 0.5,boxes2[..., :2] + boxes2[..., 2:] * 0.5], axis=-1)'''逐个位置比较boxes1_x0y0x1y1[..., :2]和boxes1_x0y0x1y1[..., 2:],即逐个位置比较[x0, y0]和[x1, y1],小的留下。比如留下了[x0, y0]这一步是为了避免一开始w h 是负数,导致x0y0成了右下角坐标,x1y1成了左上角坐标。'''boxes1_x0y0x1y1 = tf.concat([tf.minimum(boxes1_x0y0x1y1[..., :2], boxes1_x0y0x1y1[..., 2:]),tf.maximum(boxes1_x0y0x1y1[..., :2], boxes1_x0y0x1y1[..., 2:])], axis=-1)boxes2_x0y0x1y1 = tf.concat([tf.minimum(boxes2_x0y0x1y1[..., :2], boxes2_x0y0x1y1[..., 2:]),tf.maximum(boxes2_x0y0x1y1[..., :2], boxes2_x0y0x1y1[..., 2:])], axis=-1)
# 两个矩形的面积boxes1_area = (boxes1_x0y0x1y1[..., 2] - boxes1_x0y0x1y1[..., 0]) * (boxes1_x0y0x1y1[..., 3] - boxes1_x0y0x1y1[..., 1])boxes2_area = (boxes2_x0y0x1y1[..., 2] - boxes2_x0y0x1y1[..., 0]) * (boxes2_x0y0x1y1[..., 3] - boxes2_x0y0x1y1[..., 1])
# 相交矩形的左上角坐标、右下角坐标,shape 都是 (8, 13, 13, 3, 2)left_up = tf.maximum(boxes1_x0y0x1y1[..., :2], boxes2_x0y0x1y1[..., :2])right_down = tf.minimum(boxes1_x0y0x1y1[..., 2:], boxes2_x0y0x1y1[..., 2:])
# 相交矩形的面积inter_area。iouinter_section = tf.maximum(right_down - left_up, 0.0)inter_area = inter_section[..., 0] * inter_section[..., 1]union_area = boxes1_area + boxes2_area - inter_areaiou = inter_area / (union_area + K.epsilon())
# 包围矩形的左上角坐标、右下角坐标,shape 都是 (8, 13, 13, 3, 2)enclose_left_up = tf.minimum(boxes1_x0y0x1y1[..., :2], boxes2_x0y0x1y1[..., :2])enclose_right_down = tf.maximum(boxes1_x0y0x1y1[..., 2:], boxes2_x0y0x1y1[..., 2:])
# 包围矩形的对角线的平方enclose_wh = enclose_right_down - enclose_left_upenclose_c2 = K.pow(enclose_wh[..., 0], 2) + K.pow(enclose_wh[..., 1], 2)
# 两矩形中心点距离的平方p2 = K.pow(boxes1[..., 0] - boxes2[..., 0], 2) + K.pow(boxes1[..., 1] - boxes2[..., 1], 2)
# 增加av。加上除0保护防止nan。atan1 = tf.atan(boxes1[..., 2] / (boxes1[..., 3] + K.epsilon()))atan2 = tf.atan(boxes2[..., 2] / (boxes2[..., 3] + K.epsilon()))v = 4.0 * K.pow(atan1 - atan2, 2) / (math.pi ** 2)a = v / (1 - iou + v)
ciou = iou - 1.0 * p2 / enclose_c2 - 1.0 * a * vreturn ciou
以上,代码原作者也是做了一个非常详细的代码注释呀。可以看出,该函数定义和理论部分一致,特别是最后一行代码,和我们理论部分说的一模一样哈。
ciou = iou - 1.0 * p2 / enclose_c2 - 1.0 * a * v
该CIOU函数定义被用在求解总损失函数上了,我们知道YOLO V3的损失函数主要分为三部分,分别为:
(1)bounding box regression损失 (2)置信度损失 (3)分类损失
YOLO V4相较于YOLO V3,只在bounding box regression做了创新,用CIOU代替了MSE,其他两个部分没有做实质改变。其代码分别定义如下:
(1)bounding box regression损失
def loss_layer(conv, pred, label, bboxes, stride, num_class, iou_loss_thresh):conv_shape = tf.shape(conv)batch_size = conv_shape[0]output_size = conv_shape[1]input_size = stride * output_sizeconv = tf.reshape(conv, (batch_size, output_size, output_size,3, 5 + num_class))conv_raw_prob = conv[:, :, :, :, 5:]
pred_xywh = pred[:, :, :, :, 0:4]pred_conf = pred[:, :, :, :, 4:5]
label_xywh = label[:, :, :, :, 0:4]respond_bbox = label[:, :, :, :, 4:5]label_prob = label[:, :, :, :, 5:]
ciou = tf.expand_dims(bbox_ciou(pred_xywh, label_xywh), axis=-1) # (8, 13, 13, 3, 1)input_size = tf.cast(input_size, tf.float32)
# 每个预测框xxxiou_loss的权重 = 2 - (ground truth的面积/图片面积)bbox_loss_scale = 2.0 - 1.0 * label_xywh[:, :, :, :, 2:3] * label_xywh[:, :, :, :, 3:4] / (input_size ** 2)ciou_loss = respond_bbox * bbox_loss_scale * (1 - ciou) # 1. respond_bbox作为mask,有物体才计算xxxiou_loss
(2)置信度损失
# 2. respond_bbox作为mask,有物体才计算类别lossprob_loss = respond_bbox * tf.nn.sigmoid_cross_entropy_with_logits(labels=label_prob, logits=conv_raw_prob)
(3)分类损失 # 3. xxxiou_loss和类别loss比较简单。重要的是conf_loss,是一个focal_loss# 分两步:第一步是确定 grid_h * grid_w * 3 个预测框 哪些作为反例;第二步是计算focal_loss。expand_pred_xywh = pred_xywh[:, :, :, :, np.newaxis, :] # 扩展为(?, grid_h, grid_w, 3, 1, 4)expand_bboxes = bboxes[:, np.newaxis, np.newaxis, np.newaxis, :, :] # 扩展为(?, 1, 1, 1, 150, 4)iou = bbox_iou(expand_pred_xywh, expand_bboxes) # 所有格子的3个预测框 分别 和 150个ground truth 计算iou。(?, grid_h, grid_w, 3, 150)max_iou = tf.expand_dims(tf.reduce_max(iou, axis=-1), axis=-1) # 与150个ground truth的iou中,保留最大那个iou。(?, grid_h, grid_w, 3, 1)
# respond_bgd代表 这个分支输出的 grid_h * grid_w * 3 个预测框是否是 反例(背景)# label有物体,respond_bgd是0。没物体的话:如果和某个gt(共150个)的iou超过iou_loss_thresh,respond_bgd是0;如果和所有gt(最多150个)的iou都小于iou_loss_thresh,respond_bgd是1。# respond_bgd是0代表有物体,不是反例;权重respond_bgd是1代表没有物体,是反例。# 有趣的是,模型训练时由于不断更新,对于同一张图片,两次预测的 grid_h * grid_w * 3 个预测框(对于这个分支输出) 是不同的。用的是这些预测框来与gt计算iou来确定哪些预测框是反例。# 而不是用固定大小(不固定位置)的先验框。respond_bgd = (1.0 - respond_bbox) * tf.cast(max_iou < iou_loss_thresh, tf.float32)
# 二值交叉熵损失pos_loss = respond_bbox * (0 - K.log(pred_conf + K.epsilon()))neg_loss = respond_bgd * (0 - K.log(1 - pred_conf + K.epsilon()))
conf_loss = pos_loss + neg_loss# 回顾respond_bgd,某个预测框和某个gt的iou超过iou_loss_thresh,不被当作是反例。在参与“预测的置信位 和 真实置信位 的 二值交叉熵”时,这个框也可能不是正例(label里没标这个框是1的话)。这个框有可能不参与置信度loss的计算。# 这种框一般是gt框附近的框,或者是gt框所在格子的另外两个框。它既不是正例也不是反例不参与置信度loss的计算。(论文里称之为ignore)
最后对上述的三个损失取个平均即可,如下
ciou_loss = tf.reduce_mean(tf.reduce_sum(ciou_loss, axis=[1, 2, 3, 4])) # 每个样本单独计算自己的ciou_loss,再求平均值conf_loss = tf.reduce_mean(tf.reduce_sum(conf_loss, axis=[1, 2, 3, 4])) # 每个样本单独计算自己的conf_loss,再求平均值prob_loss = tf.reduce_mean(tf.reduce_sum(prob_loss, axis=[1, 2, 3, 4])) # 每个样本单独计算自己的prob_loss,再求平均值
至此,结合代码,有关YOLO V4损失函数的实战部分也就说完了!
本文结合了四个IOU损失的理论定义,以及CIOU在YOLO V4中代码定义,详细地分析了DIOU损失和CIOU损失。在当前目标检测模型中,这样的损失函数的确能够提高模型的表现,所以我认为后面这种损失函数会大量替代MSE损失函数做bounding box regression,所以弄懂并理解它们是有必要的。
✄------------------------------------------------
双一流大学研究生团队创建,一个专注于目标检测与深度学习的组织,希望可以将分享变成一种习惯。
整理不易,点赞三连!
