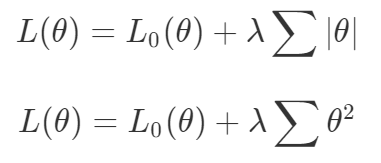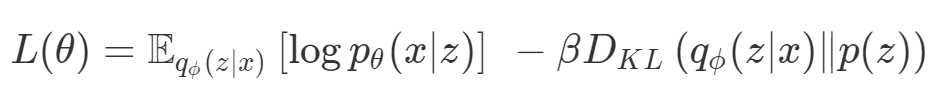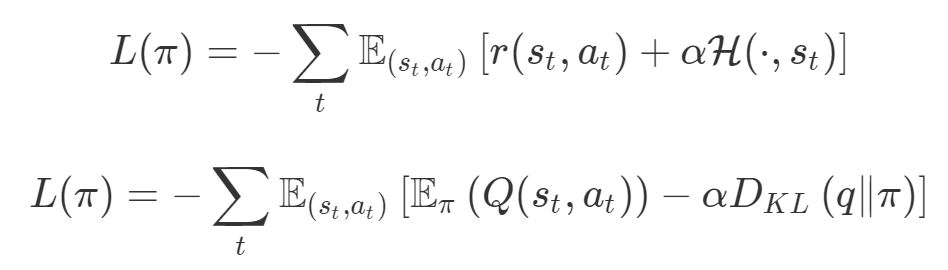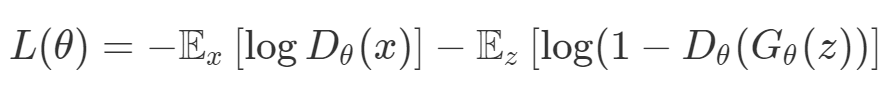本文约3500字,建议阅读9分钟
本文介绍了一些关于机器学习和线性组合的部分问题以及缓解该问题的方法。
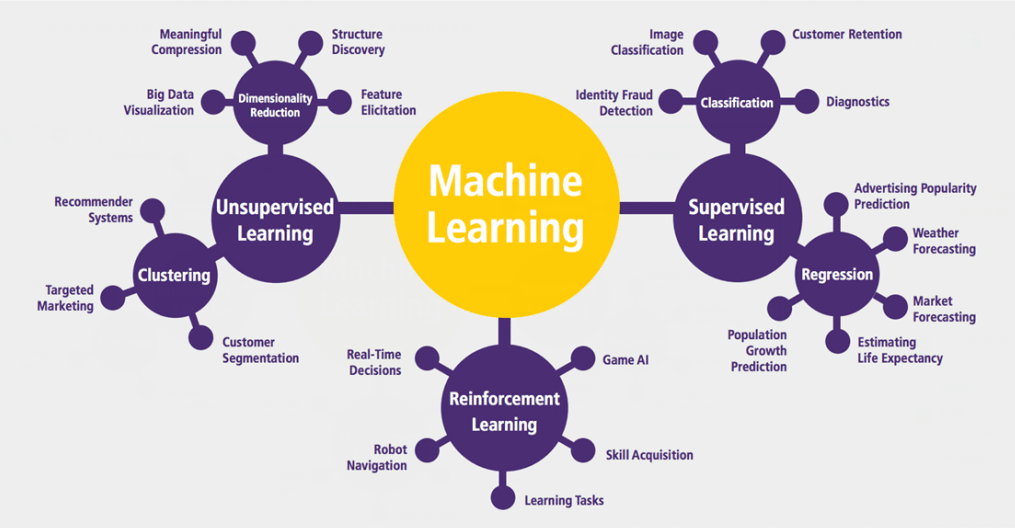
在机器学习中,损失的线性组合无处不在。虽然它们带有一些陷阱,但仍然被广泛用作标准方法。这些线性组合常常让算法难以调整。- 机器学习中的许多问题应该被视为多目标问题,但目前并非如此;
- 「1」中的问题导致这些机器学习算法的超参数难以调整;
- 检测这些问题何时发生几乎是不可能的,因此很难解决这些问题。
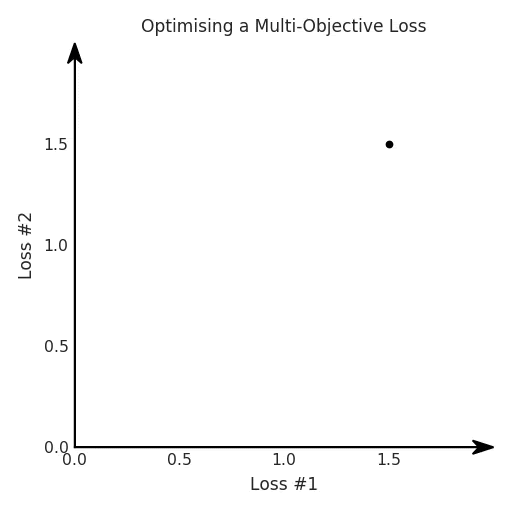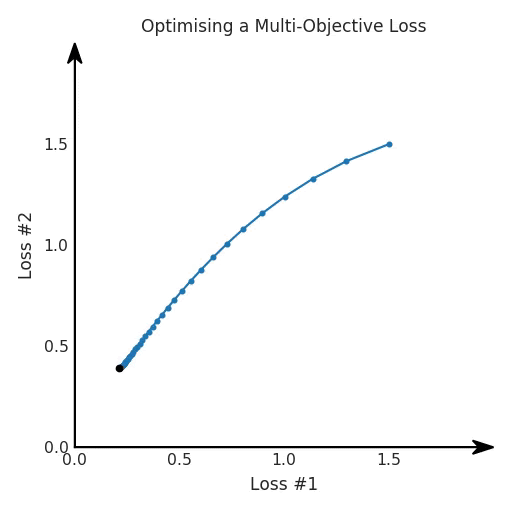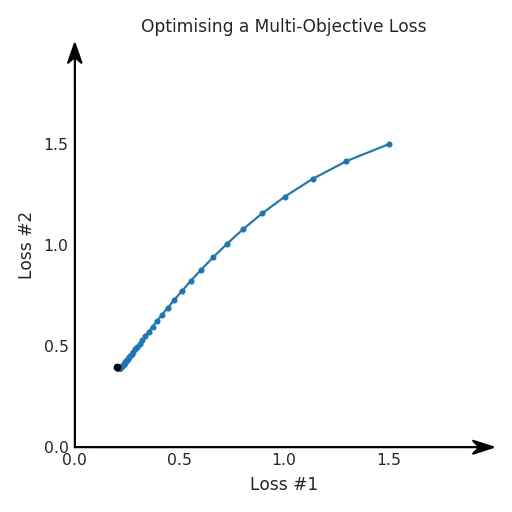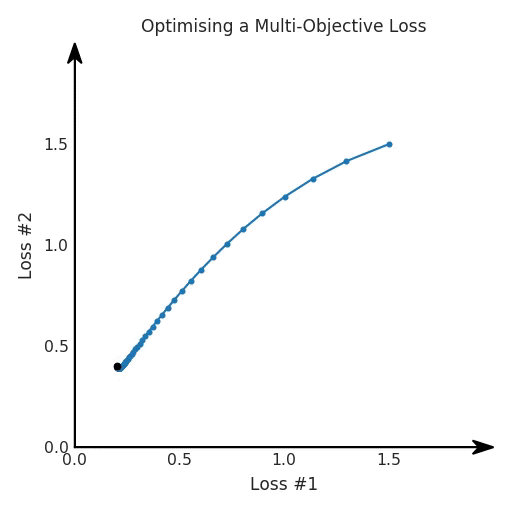
梯度下降被视为解决所有问题的一种方法。如果一种算法不能解决你的问题,那么就需要花费更多的时间调整超参数来解决问题。尽管存在单目标的问题,但通常都会对这些目标进行额外的正则化。本文作者从整个机器学习领域选择了这样的优化目标。首先来说正则化函数、权重衰减和 Lasso 算法。显然当你添加了这些正则化,你已经为你的问题创建了多目标损失。毕竟我们关心的是原始损失 L_0 和正则化损失都保持很低。你将会使用λ参数在这二者之间调整平衡。因此,损失(如 VAE 的)实际上是多目标的,第一个目标是最大程度地覆盖数据,第二个目标是保持与先前的分布接近。在这种情况下,偶尔会使用 KL 退火来引入一个可调参数β,以帮助处理这种损失的多目标性。同样在强化学习中,你也可以发现这种多目标性。在许多环境中,简单地将为达成部分目的而获得的奖励加起来很普遍。策略损失也通常是损失的线性组合。以下是 PPO、SAC 和 MPO 的策略损失及其可调整参数α的熵正则化方法。最后,GAN 损失当然是判别器损失和生成器损失的和:所有这些损失都有一些共性,研究者们正在尝试同时针对多个目标进行高效优化,并且认为最佳情况是在平衡这些通常相互矛盾的力量时找到的。在某些情况下,求和方式更加具体,并且引入了超参数以判断各部分的权重。在某些情况下,组合损失的方式有明确的理论基础,并且不需要使用超参数来调整各部分之间的平衡。一些组合损失的方法听起来很有吸引力,但实际上是不稳定且危险的。平衡行为通常更像是在「走钢丝」。考虑一个简单的情况,我们尝试对损失的线性组合进行优化。我们采用优化总损失(损失的总和)的方法,使用梯度下降来对此进行优化,观察到以下行为:def loss(θ):return loss_1(θ) + loss_2(θ)loss_derivative = grad(loss)for gradient_step in range(200): gradient = loss_derivative(θ) θ = θ - 0.02 * gradient
通常情况下,我们对两个损失之间的权衡并不满意,因此在第二个损失上引入了比例系数α,并运行了以下代码:def loss(θ, α):return loss_1(θ) + α*loss_2(θ)loss_derivative = grad(loss)for gradient_step in range(200): gradient = loss_derivative(θ, α=0.5) θ = θ - 0.02 * gradient
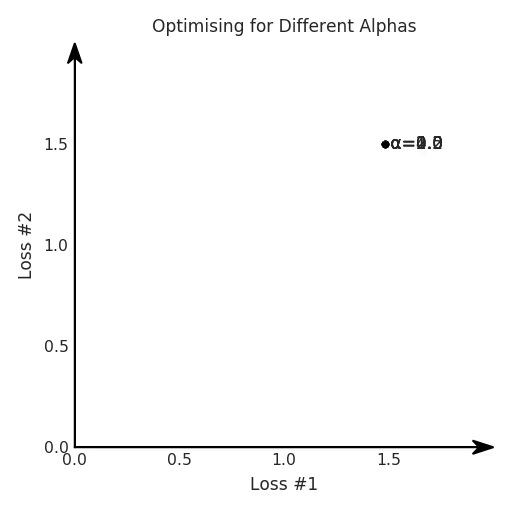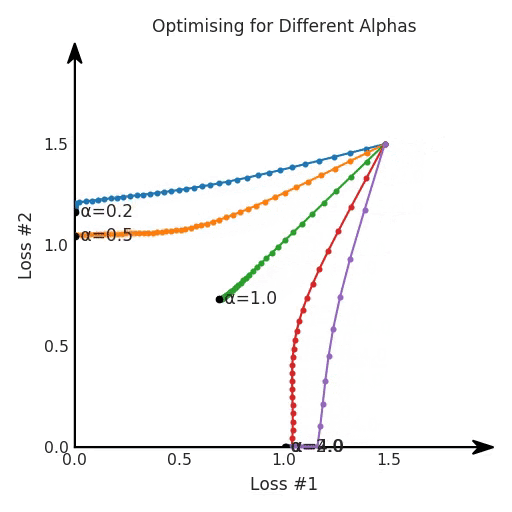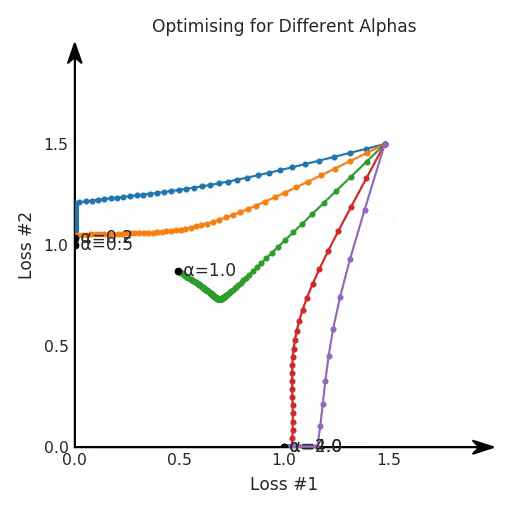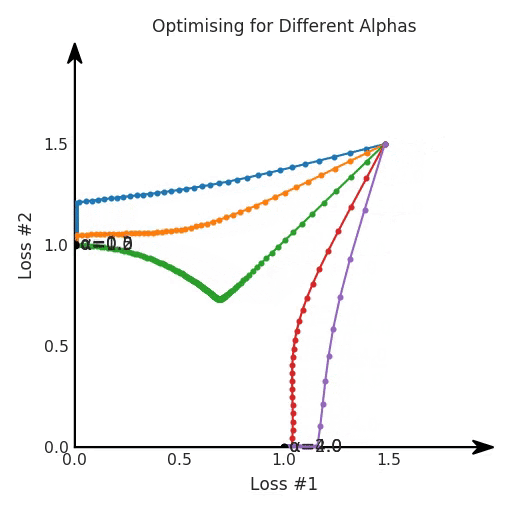
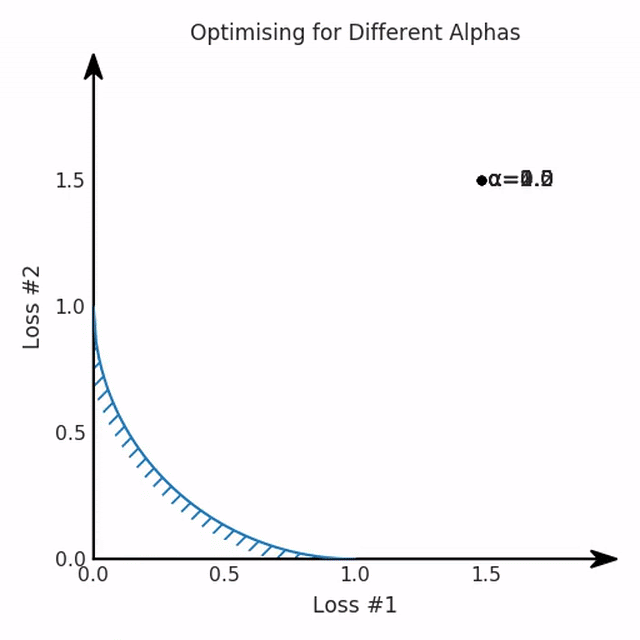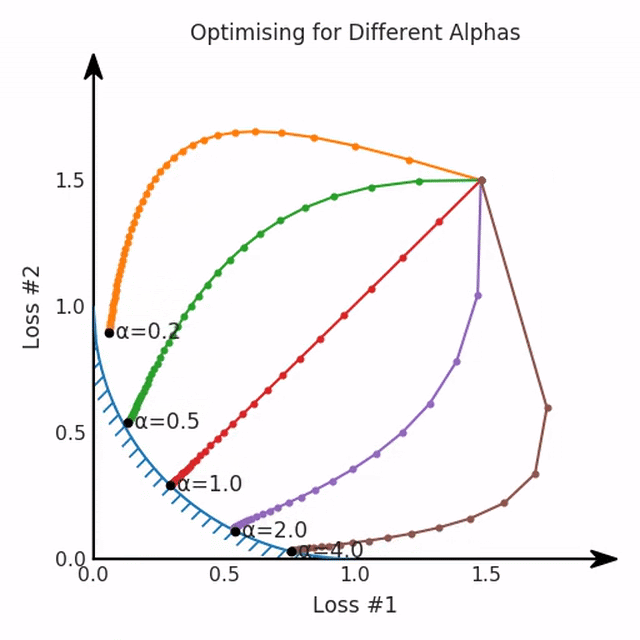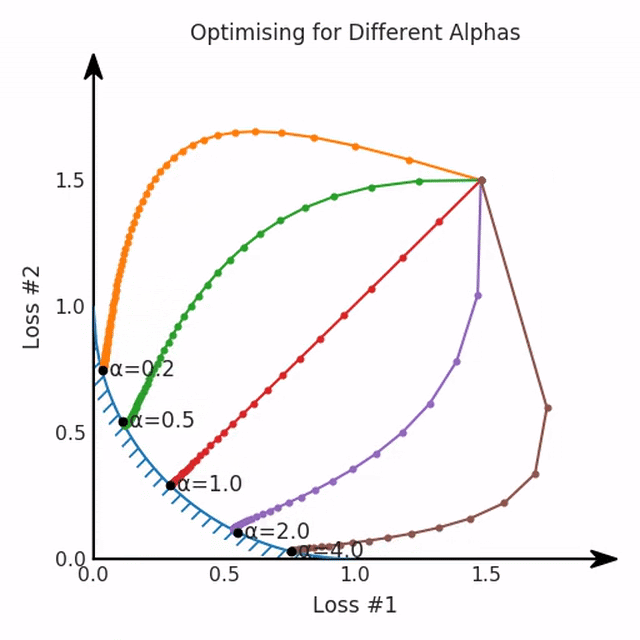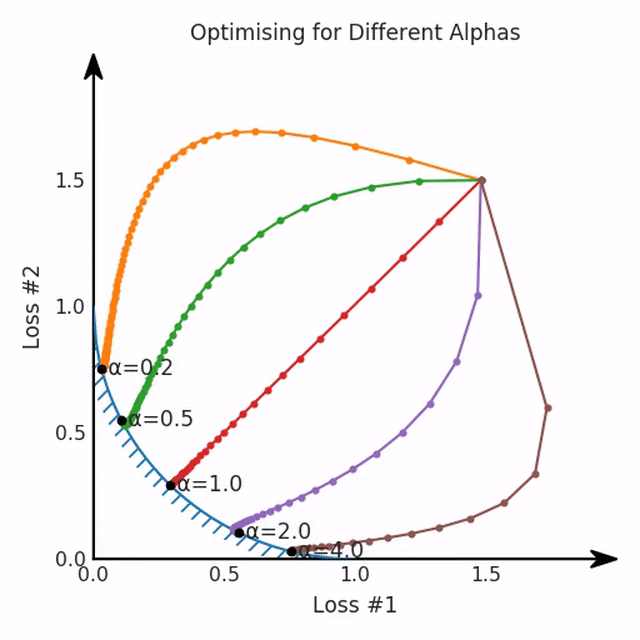
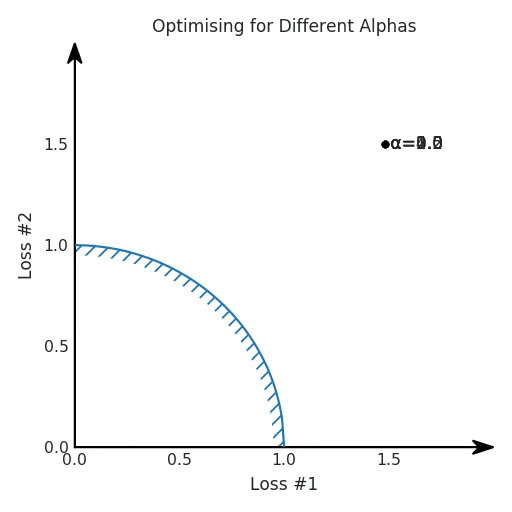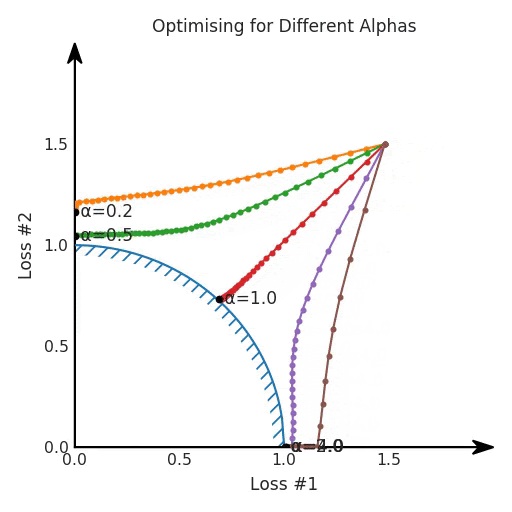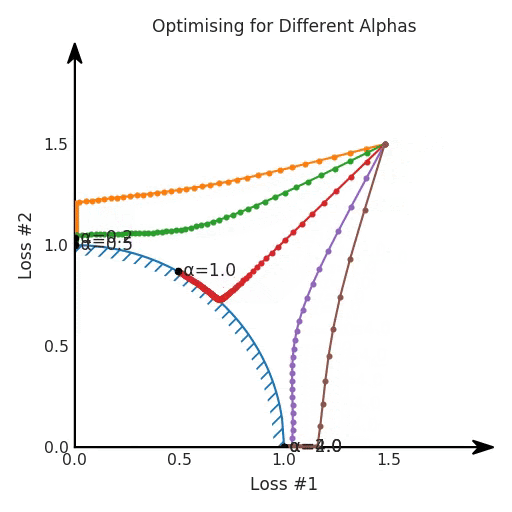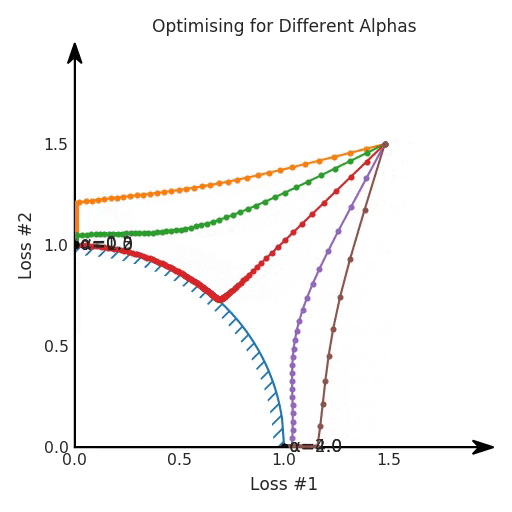
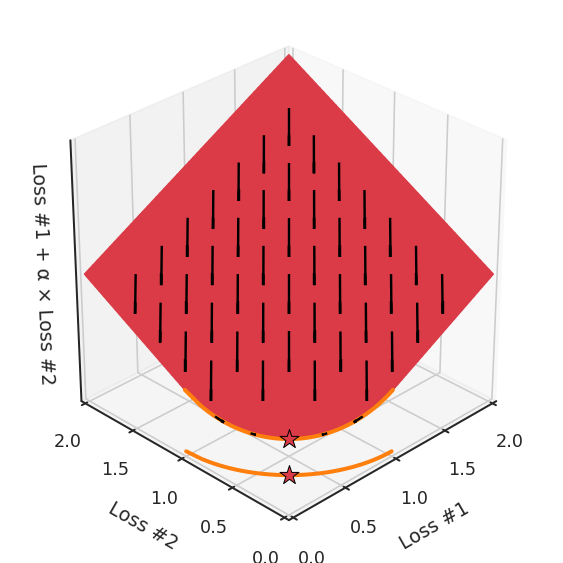
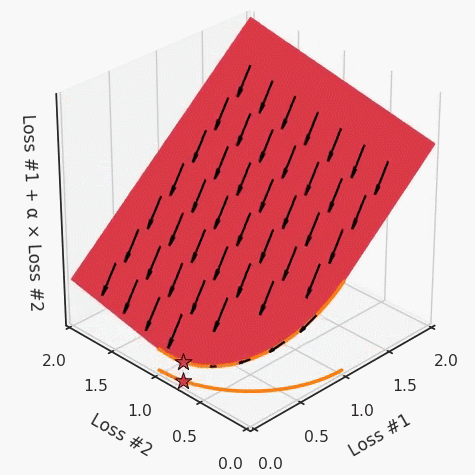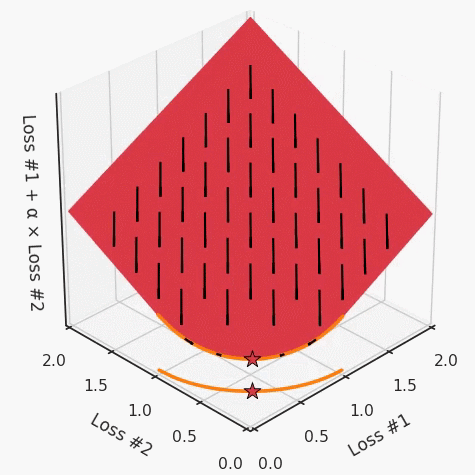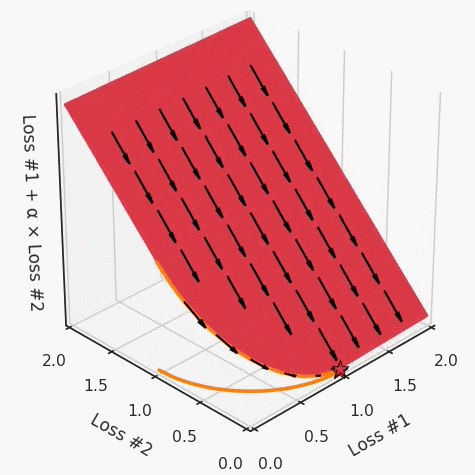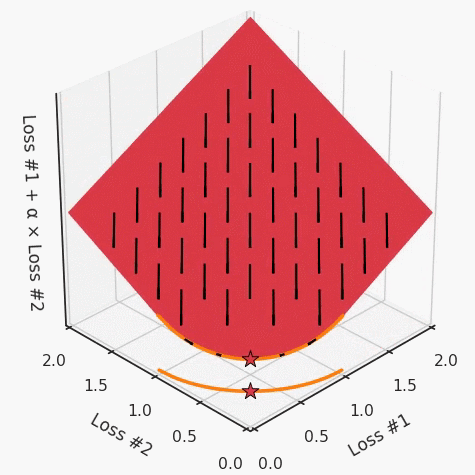
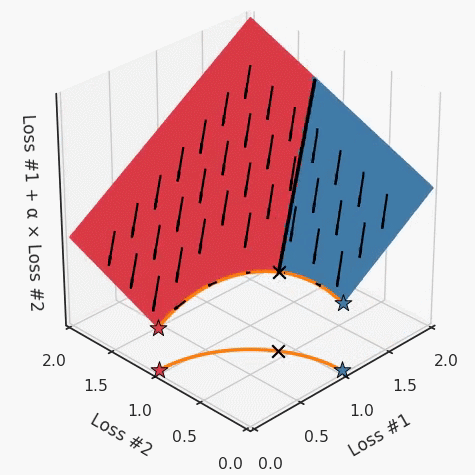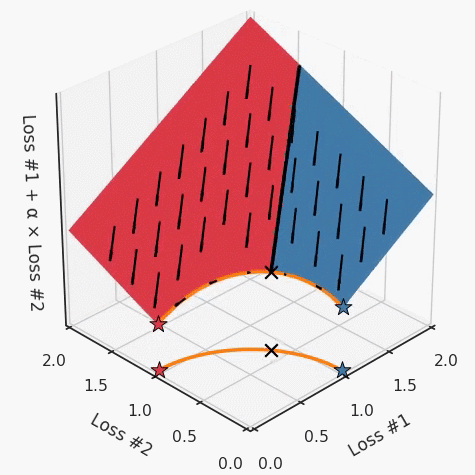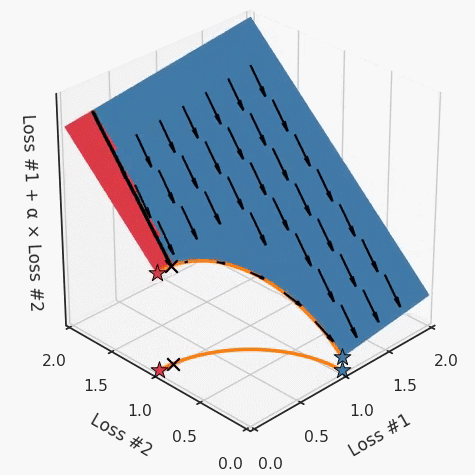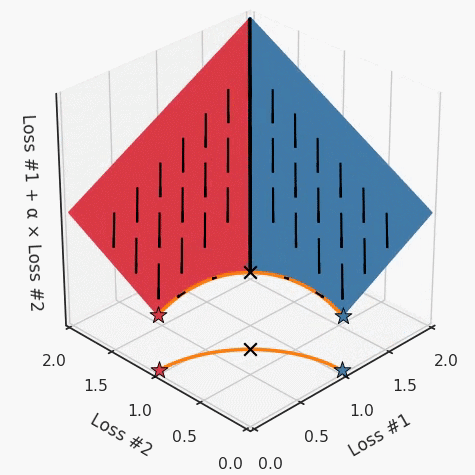
我们希望看到:当调整 α 时,可以选择两个损失之间的折衷,并选择最适合自身应用的点。我们将有效地进行一个超参数调整回路,手动选择一个α来运行优化过程,决定降低第二个损失,并相应地调整α并重复整个优化过程。经过几次迭代,我们满足于找到的解,并继续写论文。但是,事实并非总是如此。有时,问题的实际行为如下动图所示:看起来无论怎样调整参数α,都不能很好地权衡两种损失。我们看到了两类解决方案,它们都分别忽略了一种损失。但是,这两种解决方案都不适用于大多数应用。在大多数情况下,两种损失更加平衡的点是可取的解决方案。实际上,这种关于训练过程中两种损失的图表几乎从未绘制过,因此该图中所示的动态情况常常无法观察到。我们只观察绘制总体损失的训练曲线,并且得出超参数需要更多时间调整的结论。也许我们可以采取一种早停法(early stopping),以使得论文中的数据是有效的。毕竟,审稿人喜欢高效的数据。问题出在哪里呢?为什么这种方法有时有效,有时却无法提供可调参数?为此,我们需要更深入地研究一下以下两个动图之间的差异。它们都是针对相同的问题,使用相同的损失函数生成的,并且正在使用相同的优化方法来优化这些损失。因此,这些都不是造成差异的原因。在这些问题之间发生变化的是模型。换句话说,模型参数θ对模型输出的影响是不同的。因此,让我们可视化一下通常不可见的东西,这是两个优化的帕累托前沿。这是模型可以实现且是不受其他任何解决方案支配的解决方案的集合。换句话说,这是一组可实现的损失,没有一个点可以使所有损失都变得更好。无论你如何选择在两个损失之间进行权衡,首选的解决方案始终依赖帕累托前沿。通常,通过调整损失的超参数,你通常希望仅在同一个前沿找到一个不同的点。两个帕累托前沿之间的差异会使得第一种情况的调优效果很好,但是在更改模型后却严重失败了。事实证明,当帕累托前沿为凸形时,我们可以通过调整α参数来实现所有可能的权衡效果。但是,当帕累托前沿为凹形时,该方法似乎不再有效。通过查看第三个维度中的总体损失,可以发现实际上是用梯度下降优化了损失。在下图中,我们可视化了相对于每个损失的总损失平面。实际上是使用参数的梯度下降到该平面上,采取的每个梯度下降步骤也必将在该平面上向下移动。你可以想象成梯度下降优化过程是在该平面上放置一个球形小卵石,使其在重力作用下向下移动直到它停下来。优化过程停止的点是优化过程的结果,此处用星星表示。如下图所示,无论你如何上下摆动该平面,最终都将得到最佳结果。通过调整α,此空间将保持一个平面。毕竟更改α只会更改该平面的倾斜度。在凸的情况下,可以通过调整α来实现帕累托曲线上的任何解。α大一点会将星星拉到左侧,α小一点会将星星拉到右侧。优化过程的每个起点都将在相同的解上收敛,这对于α的所有值都是正确的。但是,如果我们看一下具有凹帕累托前沿面的不同模型问题,那么问题出现在哪里就变得显而易见了。如果我们想象卵石遵循该平面上的梯度:有时向左滚动更多,有时向右滚动更多,但始终向下滚动。然后很明显它最终将到达两个角点之一,即红色星或蓝色星。当我们调整α时,该平面以与凸情况下完全相同的方式倾斜,但由于帕累托前沿面的形状,将永远只能到达该前沿面上的两个点,即凹曲线末端的两个点。使用基于梯度下降方法无法找到曲线上的 × 点(实际上想要达到的点)。为什么?因为这是一个鞍点(saddle point)。同样要注意的是,当我们调整α时会发生什么。我们可以观察到,相对于其他解,一个解需要调整多少个起点,但我们无法调整以找到帕累托前沿面上的其他解。第一,即使没有引入超参数来权衡损失,说梯度下降试图在反作用力之间保持平衡也是不正确的。根据模型可实现的解,可以完全忽略其中一种损失,而将注意力放在另一种损失上,反之亦然,这取决于初始化模型的位置;
第二,即使引入了超参数,也将在尝试后的基础上调整此超参数。研究中往往是运行一个完整的优化过程,然后确定是否满意,再对超参数进行微调。重复此优化循环,直到对性能满意为止。这是一种费时费力的方法,通常涉及多次运行梯度下降的迭代;
第三,超参数不能针对所有的最优情况进行调整。无论进行多少调整和微调,你都不会找到可能感兴趣的中间方案。这不是因为它们不存在,它们一定存在,只是因为选择了一种糟糕的组合损失方法;
第四,必须强调的是,对于实际应用,帕累托前沿面是否为凸面以及因此这些损失权重是否可调始终是未知的。它们是否是好的超参数,取决于模型的参数化方式及其影响帕累托曲线的方式。但是,对于任何实际应用,都无法可视化或分析帕累托曲线。可视化比原始的优化问题要困难得多。因此出现问题并不会引起注意;
最后,如果你真的想使用这些线性权重来进行权衡,则需要明确证明整个帕累托曲线对于正在使用的特定模型是凸的。因此,使用相对于模型输出而言凸的损失不足以避免问题。如果参数化空间很大(如果优化涉及神经网络内部的权重,则情况总是如此),你可能会忘记尝试这种证明。需要强调的是,基于某些中间潜势(intermediate latent),显示这些损失的帕累托曲线的凸度不足以表明你具有可调参数。凸度实际上需要取决于参数空间以及可实现解决方案的帕累托前沿面。
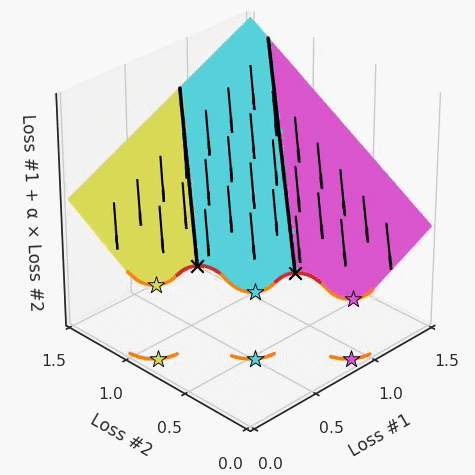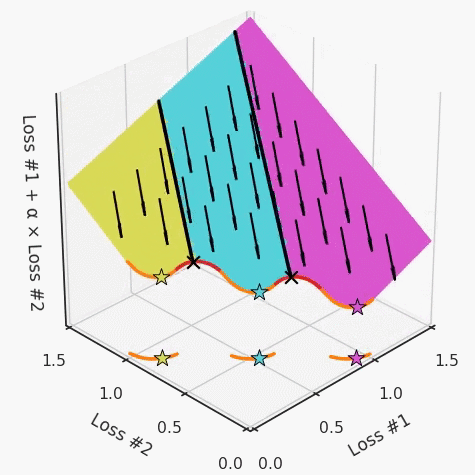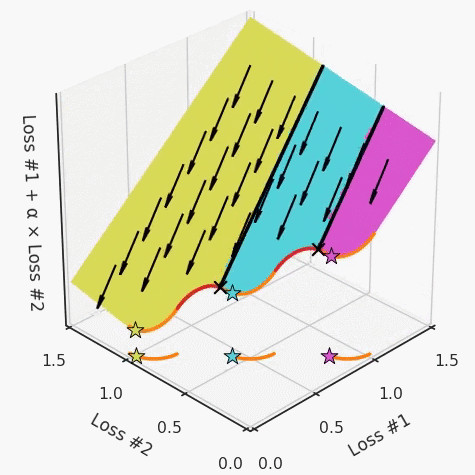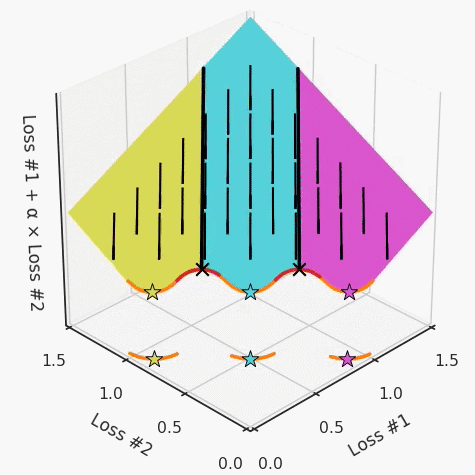
请注意,在大多数应用中,帕累托前沿面既不是凸的也不是凹的,而是二者的混合体,这扩大了问题。以一个帕累托前沿面为例,凸块之间有凹块。每个凹块不仅可以确保无法通过梯度下降找到解,还可以将参数初始化的空间分成两部分,一部分可以在一侧的凸块上找到解,而另一部分智能在另一侧上找到解。如下动图所示,在帕累托前沿面上有多个凹块会使问题更加复杂。因此,我们不仅具有无法找到所有解的超参数α,而且根据初始化,它可能会找到帕累托曲线的不同凸部分。此参数和初始化以令人困惑的方式相互混合,这让问题更加困难。如果稍微调整参数以希望稍微移动最优值,则即使保持相同的初始化,也可能会突然跳到帕累托前沿面的其他凸部分。https://engraved.ghost.io/why-machine-learning-algorithms-are-hard-to-tune/
编辑:黄继彦
校对:林亦霖