【特征工程】17种将离散特征转化为数字特征的方法
作者 | Samuele Mazzanti
编译 | VK
来源 | Towards Data Science
“你知道哪种梯度提升算法?”
“Xgboost,LightGBM,Catboost,HistGradient。”
“你知道哪些离散变量的编码?”
“one-hot”
在一次数据科学面试中听到这样的对话我不会感到惊讶。不过,这将是相当惊人的,「因为只有一小部分数据科学项目涉及机器学习,而实际上所有这些项目都涉及一些离散数据」。
❝离散变量的编码是将一个离散列转换为一个(或多个)数字列的过程。
❞
这是必要的,因为计算机处理数字比处理字符串更容易。为什么?因为用数字很容易找到关系(比如“大”、“小”、“双”、“半”)。然而,当给定字符串时,计算机只能说出它们是“相等”还是“不同”。
然而,尽管离散变量的编码有影响,但它很容易被数据科学从业者忽视。
❝离散变量的编码是一个令人惊讶的被低估的话题。
❞
这就是为什么我决定深化编码算法的知识。我从一个名为“category_encoders”的Python库开始(这是Github链接:https://github.com/scikit-learn-contrib/category_encoders)。使用它非常简单:
!pip install category_encoders
import category_encoders as ce
ce.OrdinalEncoder().fit_transform(x)
这篇文章是对库中包含的17种编码算法的演练。对于每种算法,我用几行代码提供了简短的解释和Python实现。其目的不是要重新发明轮子,而是要认识到算法是如何工作的。毕竟,
❝“除非你能写代码,否则你不懂”。
❞
并非所有编码都是相同的
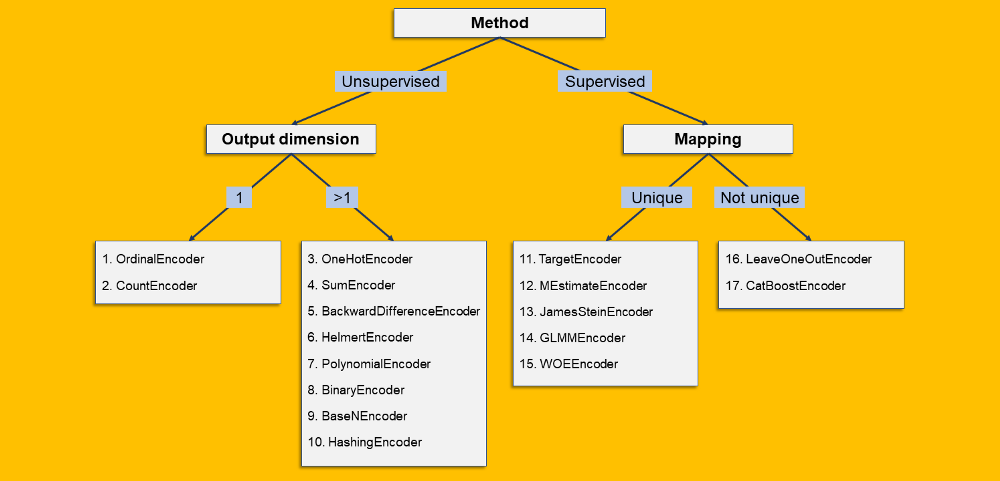
我根据17种编码算法的一些特点对它们进行了分类。类似决策树:

分割点为:
「监督/无监督」:当编码完全基于离散列时,它是无监督的。如果编码是基于原始列和第二列(数字)的某个函数,则它是监督的。 「输出维度」:分类列的编码可能产生一个数值列(输出维度=1)或多个数值列(输出维度>1)。 「映射」:如果每个等级都有相同的输出-无论是标量(例如OrdinalEncoder)还是数组(例如onehotcoder),那么映射是唯一的。相反,如果允许同一等级具有不同的可能输出,则映射不是唯一的。
17种离散编码算法
1.「OrdinalEncoder」
每个等级都映射到一个整数,从1到L(其中L是等级数)。在这种情况下,我们使用了字母顺序,但任何其他自定义顺序都是可以接受的。
sorted_x = sorted(set(x))
ordinal_encoding = x.replace(dict(zip(sorted_x, range(1, len(sorted_x) + 1))))

你可能认为该编码是没有意义的,尤其是当等级没有内在顺序的时候。你是对的!实际上,它只是一种方便的表示,通常用于节省内存,或作为其他类型编码的中间步骤。
2.CountEncoder
每个等级都映射到该级别的观察数。
count_encoding = x.replace(x.value_counts().to_dict())
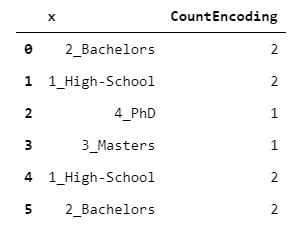
这种编码可以作为每个级别的“可信度”的指标。例如,一个机器学习算法可能会自动决定只考虑其计数高于某个阈值的级别所带来的信息。
3.OneHotEncoder
编码算法中最常用的。每个级别映射到一个伪列(即0/1的列),指示该行是否携带属于该级别。
one_hot_encoding = ordinal_encoding.apply(lambda oe: pd.Series(np.diag(np.ones(len(set(x))))[oe - 1].astype(int)))
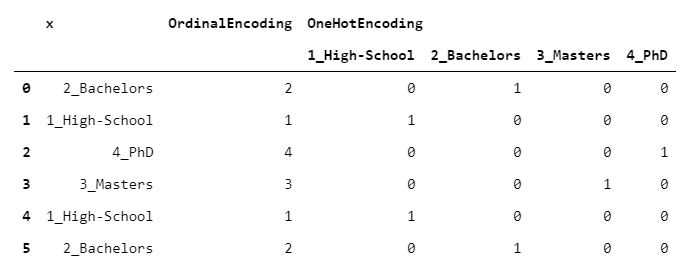
这意味着,虽然你的输入是一个单独的列,但是你的输出由L列组成(原始列的每个级别对应一个列)。这就是为什么OneHot编码应该小心处理:你最终得到的数据帧可能比原来的大得多。
一旦数据是OneHot编码,它就可以用于任何预测算法。为了使事情一目了然,让我们对每一个等级进行一次观察。
假设我们观察到一个目标变量,叫做y,包含每个人的收入(以千美元计)。让我们用线性回归(OLS)来拟合数据。
为了使结果易于阅读,我在表的侧面附加了OLS系数。
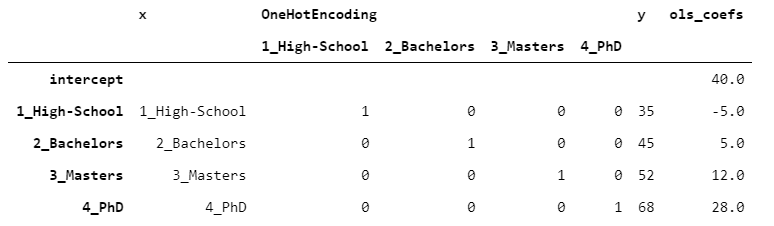
在OneHot编码的情况下,截距没有特定的意义。在这种情况下,由于我们每层只有一个观测值,通过加上截距和乘上系数,我们得到y的精确值(没有误差)。
4.SumEncoder
下面的代码一开始可能有点晦涩难懂。但是不要担心:在这种情况下,理解如何获得编码并不重要,而是如何使用它。
sum_encoding = one_hot_encoding.iloc[:, :-1].apply(lambda row: row if row.sum() == 1 else row.replace(0, -1), axis = 1)
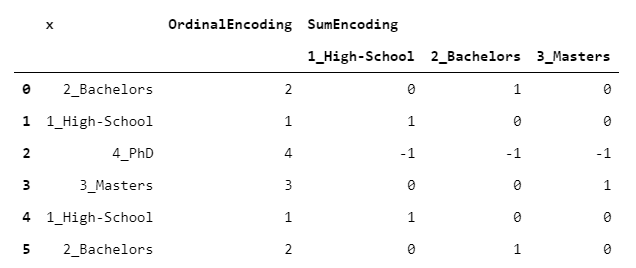
SumEncoder属于一个名为“对比度编码”的类。这些编码被设计成在回归问题中使用时具有特定的行为。换句话说,如果你想让回归系数有一些特定的属性,你可以使用其中的一种编码。
特别是,当你希望回归系数加起来为0时,使用SumEncoder。如果我们采用之前的相同数据并拟合OLS,我们得到的结果是:
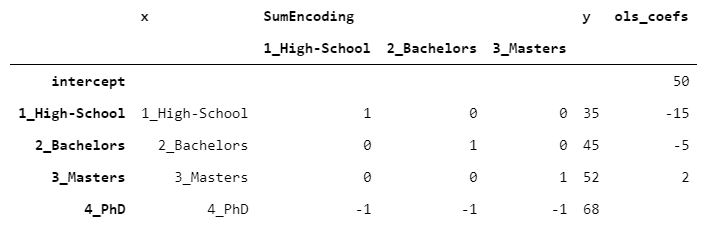
这一次,截距对应于y的平均值。此外,通过取最后一级的y并从截距(68-50)中减去它,我们得到18,这与剩余系数之和(-15-5+2=-18)正好相反。这正是我前面提到的SumEncoder的属性。
5.BackwardDifferenceEncoder
另一种对比度编码。
这个编码器对序数变量很有用,也就是说,可以用有意义的方式对其等级进行排序的变量。BackwardDifferenceEncoder设计用于比较相邻的等级。
backward_difference_encoding = ordinal_encoding.apply(
lambda oe: pd.Series(
[i / len(set(x)) for i in range(1, oe)] + [- i / len(set(x)) for i in range(len(set(x)) - oe, 0, -1)]))
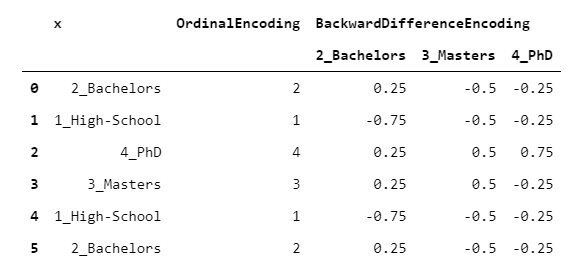
假设你有一个有序变量(例如教育水平),你想知道它与一个数字变量(例如收入)之间的关系。比较每一个连续的水平(例如学士与高中,硕士与学士)与目标变量的关系可能很有趣。这就是BackwardDifferenceEncoder的设计目的。让我们看一个例子,使用相同的数据。
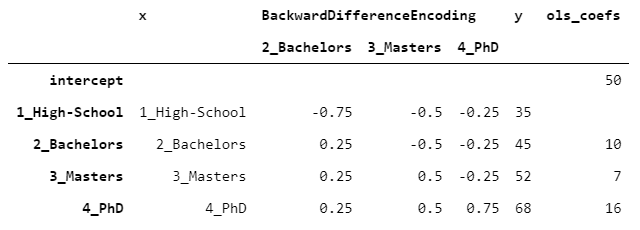
截距与y的平均值一致。学士的系数为10,因为学士的y比高中高10,硕士的系数等于7,因为硕士的y比单身汉高7,依此类推。
6.HelmertEncoder
HelmertEncoder与BackwardDifferenceEncoder非常相似,但不是只与前一个进行比较,而是将每个级别与之前的所有级别进行比较。
helmert_encoding = ordinal_encoding.apply(
lambda oe: pd.Series([0] * (oe - 2) + ([oe - 1] if oe > 1 else []) + [-1] * (len(set(x)) - oe))
).div(pd.Series(range(2,len(set(x)) + 1)))
 ]
]
让我们看看OLS模型能给我们带来什么:
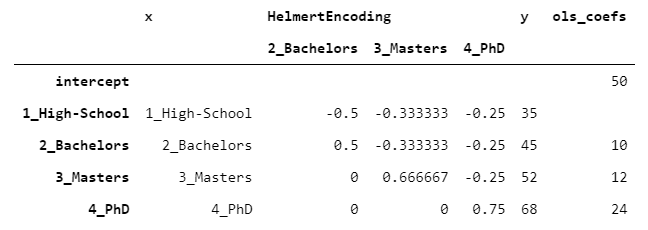
PhD的系数是24,因为PhD比之前水平的平均值高24-((35+45+52)/3)=24。同样的道理适用于所有的等级。
7.PolynomialEncoder
另一种对比编码。
顾名思义,PolynomialEncoder被设计用来量化目标变量相对于离散变量的线性、二次和三次行为。
def do_polynomial_encoding(order):
# 代码来自https://github.com/pydata/patsy/blob/master/patsy/contrasts.py
n = len(set(x))
scores = np.arange(n)
scores = np.asarray(scores, dtype=float)
scores -= scores.mean()
raw_poly = scores.reshape((-1, 1)) ** np.arange(n).reshape((1, -1))
q, r = np.linalg.qr(raw_poly)
q *= np.sign(np.diag(r))
q /= np.sqrt(np.sum(q ** 2, axis=1))
q = q[:, 1:]
return q[order - 1]
polynomial_encoding = ordinal_encoding.apply(lambda oe: pd.Series(do_polynomial_encoding(oe)))
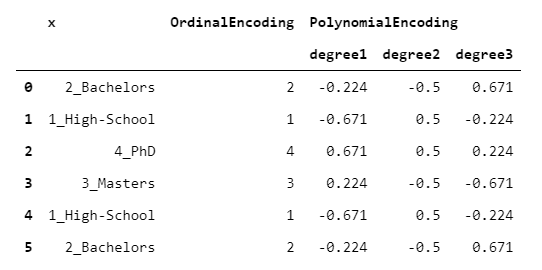
我知道你在想什么。一个数值变量如何与一个非数值变量有线性(或二次或三次)关系?这是基于这样一个假设,即潜在的离散变量不仅具有顺序性,而且具有等间距。
基于这个原因,我建议谨慎使用它,只有当你确信这个假设是合理的。
8.BinaryEncoder
BinaryEncoder 与OrdinalEncoder基本相同,唯一的区别是将整数转换成二进制数,然后每个位置数字都是one-hot编码。
binary_base = ordinal_encoding.apply(lambda oe: str(bin(oe))[2:].zfill(len(bin(len(set(x)))) - 2))
binary_encoding = binary_base.apply(lambda bb: pd.Series(list(bb))).astype(int)

输出由伪列组成,就像OneHotEncoder的情况一样,但是它会导致相对于one-hot的维数降低。
老实说,我不知道这种编码有什么实际应用。
9.BaseNEncoder
BaseNEncoder只是BinaryEncoder的一个推广。实际上,在BinaryEncoder中,数字以2为基数,而在BaseNEncoder中,数字以n为底,n大于1。
def int2base(n, base):
out = ''
while n:
out += str(int(n % base))
n //= base
return out[::-1]
base_n = ordinal_encoding.apply(lambda oe: int2base(n = oe, base = base))
base_n_encoding = base_n.apply(lambda bn: pd.Series(list(bn.zfill(base_n.apply(len).max())))).astype(int)
让我们看一个base=3的例子。
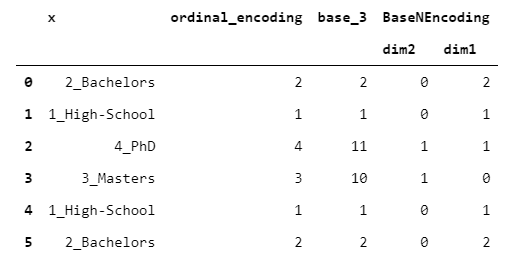
老实说,我不知道这种编码有什么实际应用。
10.HashingEncoder
在HashingEncoder中,每个原始级别都使用一些哈希算法(如SHA-256)进行哈希处理。然后,将结果转换为整数,并取该整数相对于某个(大)除数的模。通过这样做,我们将每个原始字符串映射到一个某个范围的整数。最后,这个过程得到的整数是one-hot编码的。
def do_hash(string, output_dimension):
hasher = hashlib.new('sha256')
hasher.update(bytes(string, 'utf-8'))
string_hashed = hasher.hexdigest()
string_hashed_int = int(string_hashed, 16)
string_hashed_int_remainder = string_hashed_int % output_dimension
return string_hashed, string_hashed_int, string_hashed_int_remainder
hashing = x.apply(
lambda string: pd.Series(do_hash(string, output_dimension),
index = ['x_hashed', 'x_hashed_int', 'x_hashed_int_remainder']))
hashing_encoding = hashing['x_hashed_int_remainder'].apply(lambda rem: pd.Series(np.diag(np.ones(output_dimension))[rem])).astype(int)
让我们看一个输出维数为10的示例。

散列的基本特性是得到的整数是均匀分布的。所以,如果除数足够大,两个不同的字符串不太可能映射到同一个整数。那为什么有用呢?实际上,这有一个非常实际的应用叫做“哈希技巧”。
假设你希望使用逻辑回归来生成电子邮件垃圾邮件分类器。你可以通过对数据集中包含的所有单词进行ONE-HOT编码来实现这一点。主要的缺点是你需要将映射存储在单独的字典中,并且你的模型维度将在新字符串出现时发生更改。
使用散列技巧可以很容易地克服这些问题,因为通过散列输入,你不再需要字典,并且输出维是固定的(它只取决于你最初选择的除数)。此外,对于散列的属性,你可以认为新字符串可能具有与现有字符串不同的编码。
11.TargetEncoder
假设有两个变量:一个是离散变量(x),一个是数值变量(y)。假设你想把x转换成一个数值变量。你可能需要使用y“携带”的信息。一个明显的想法是取x的每个级别的y的平均值。在公式中:

这是合理的,但是这种方法有一个很大的问题:有些群体可能太小或太不稳定而不可靠。许多有监督编码通过在组平均值和y的全局平均值之间选择一种中间方法来克服这个问题:
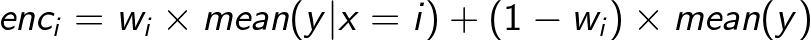
其中$w_i$在0和1之间,取决于组的“可信”程度。
接下来的三种算法(TargetEncoder、MEstimateEncoder和JamesSteinEncoder)根据它们定义$w_i$的方式而有所不同。
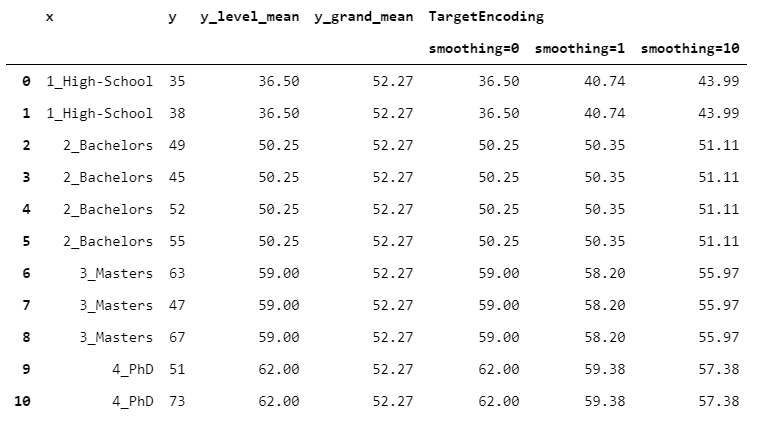
在TargetEncoder中,权重取决于组的数量和一个称为“平滑”的参数。当“平滑”为0时,我们仅依赖组平均值。然后,随着平滑度的增加,全局平均权值越来越多,导致正则化更强。
y_mean = y.mean()
y_level_mean = x.replace(y.groupby(x).mean())
weight = 1 / (1 + np.exp(-(count_encoding - 1) / smoothing))
target_encoding = y_level_mean * weight + y_mean * (1 - weight)
让我们看看结果如何随着一些不同的平滑值而变化。
12.MEstimateEncoder
MEstimateEncoder类似于TargetEncoder,但$w_i$取决于一个名为“m”的参数,该参数设置全局平均值的绝对权重。m很容易理解,因为它可以被视为若干个观测值:如果等级正好有m个观测值,那么等级平均值和总体平均权重是相同的。
y_mean = y.mean()
y_level_mean = x.replace(y.groupby(x).mean())
weight = count_encoding / (count_encoding + m)
m_estimate_encoding = y_level_mean * weight + y_grand_mean * (1 - weight)
让我们看看不同m值的结果是如何变化的:

13.「JamesSteinEncoder」
TargetEncoder和MEstimateEncoder既取决于组的数量,也取决于用户设置的参数值(分别是smoothing和m)。这不方便,因为设置这些权重是一项手动任务。
一个自然的问题是:有没有一种方法可以在不需要任何人为干预的情况下,设定一个最佳的工作环境?JamesSteinEncoder试图以一种基于统计数据的方式来做到这一点。
y_mean = y.mean()
y_var = y.var()
y_level_mean = x.replace(y.groupby(x).mean())
y_level_var = x.replace(y.groupby(x).var())
weight = 1 - (y_level_var / (y_var + y_level_var) * (len(set(x)) - 3) / (len(set(x)) - 1))
james_stein_encoding = y_level_mean * weight + y_mean * (1 - weight)
直觉是,一个高方差的群体的平均值应该不那么可信。因此,群体方差越高,权重就越低(如果你想知道更多关于公式的知识,我建议克里斯•赛义德的这篇文章)。
让我们看一个数值示例:

JamesSteinEncoder有两个显著的优点:它提供比最大似然估计更好的估计,并且不需要任何参数设置。
14.GLMMEncoder
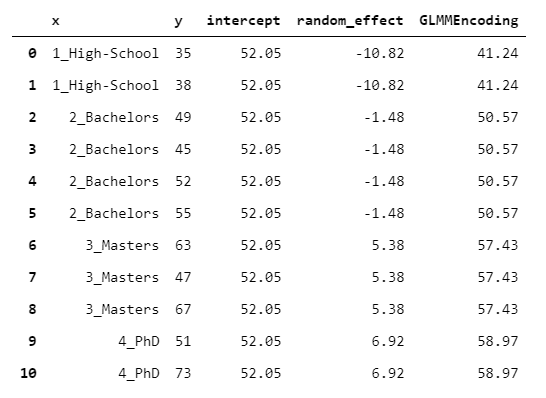
GLMMEncoder采用一种完全不同的方法。
基本上,它拟合y上的线性混合效应模型。这种方法利用了一个事实,即线性混合效应模型是为处理同质观察组而精心设计的。因此,我们的想法是拟合一个没有回归变量(只有截距)的模型,并使用层次作为组。
然后,输出就是截距和随机效应的总和。
model = smf.mixedlm(formula = 'y ~ 1', data = y.to_frame(), groups = x).fit()
intercept = model.params['Intercept']
random_effect = x.replace({k: float(v) for k, v in model.random_effects.items()})
glmm_encoding = intercept + random_effect
15.WOEEncoder
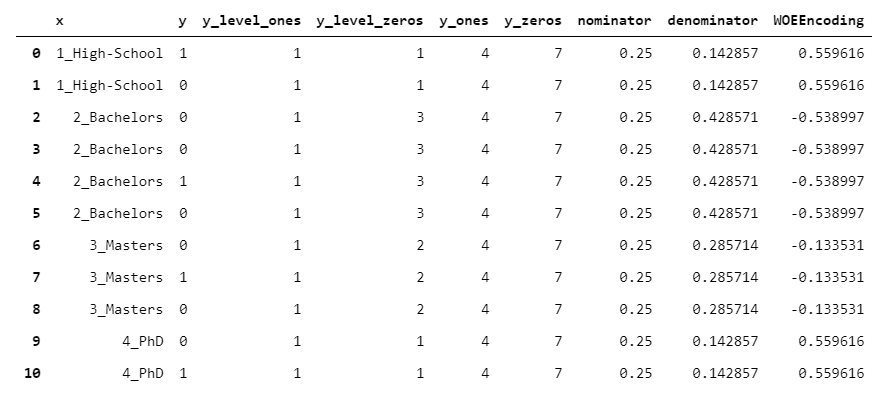
WOEEncoder(代表“证据权重 Weight of Evidence”编码器)只能用于二元变量,即级别为0/1的目标变量。
证据权重背后的想法是你有两种分布:
1的分布(每组1的个数/y中1的个数) 0的分布(每组0的个数/y中0的个数)
该算法的核心是将1的分布除以0的分布(对于每个组)。当然,这个值越高,我们就越有信心认为这个基团“偏向”1,反之亦然。然后,取该值的对数。
y_level_ones = x.replace(y.groupby(x).apply(lambda l: (l == 1).sum()))
y_level_zeros = x.replace(y.groupby(x).apply(lambda l: (l == 0).sum()))
y_ones = (y == 1).sum()
y_zeros = (y == 0).sum()
nominator = y_level_ones / y_ones
denominator = y_level_zeros / y_zeros
woe_encoder = np.log(nominator / denominator)
如你所见,由于公式中存在对数,因此无法直接解释输出。然而,它作为机器学习的一个预处理步骤工作得很好。
16.LeaveOneOutEncoder
到目前为止,所有的15个编码器都有一个唯一的映射。
但是,如果你计划使用编码作为预测模型的输入(例如GB),这可能是一个问题。实际上,假设你使用TargetEncoder。这意味着你在X_train中引入了关于y_train的信息,这可能会导致严重的过拟合风险。
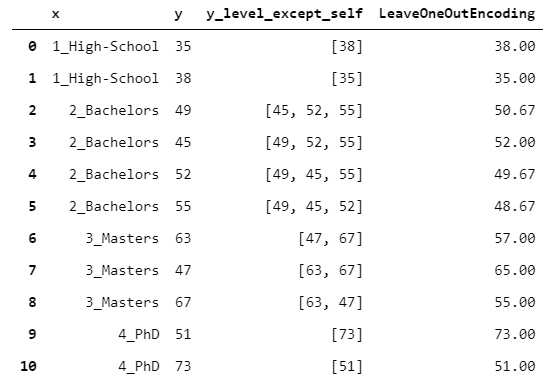
关键是:如何在限制过拟合的风险的同时保持有监督的编码?LeaveOneOutEncoder提供了一个出色的解决方案。它执行普通的目标编码,但是对于每一行,它不考虑该行观察到的y值。这样,就避免了行方向的泄漏。
y_level_except_self = x.to_frame().apply(lambda row: y[x == row['x']].drop(row.name).to_list(), axis = 1)
leave_one_out_encoding = y_level_except_self.apply(np.mean)
17.CatBoostEncoder
CatBoost是一种梯度提升算法(如XGBoost或LightGBM),它在许多问题中都表现得非常好。
CatboostEncoder的工作原理基本上类似于LeaveOneOutEncoder,但是是一个在线方法。
但是如何模拟在线行为?想象一下你有一张桌子。然后,在桌子中间的某个地方划一排。CatBoost所做的是假装当前行上方的行已经被及时观察到,而下面的行还没有被观察到(即将来会观察到)。然后,该算法执行leave one out编码,但仅基于已观察到的行。
y_mean = y.mean()
y_level_before_self = x.to_frame().apply(lambda row: y[(x == row['x']) & (y.index < row.name)].to_list(), axis = 1)
catboost_encoding = y_level_before_self.apply(lambda ylbs: (sum(ylbs) + y_mean * a) / (len(ylbs) + a))

这似乎有些荒谬。为什么要抛弃一些可能有用的信息呢?你可以将其简单地视为对输出进行随机化的更极端尝试(例如,减少过拟合)。
谢谢你的阅读!我希望你觉得这篇文章有用。
往期精彩回顾
获取本站知识星球优惠券,复制链接直接打开:
https://t.zsxq.com/qFiUFMV
本站qq群704220115。
加入微信群请扫码:
