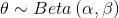【深度好文】Python实现 "贝叶斯" 统计推断！

——皮埃尔—西蒙•拉普拉斯

本文我们将学习贝叶斯统计中的核心概念以及一些用于贝叶斯分析的基本工具。大部分内容都是一些理论介绍，其中会涉及一些Python代码，尽管本文内容有点偏理论，可能会让习惯代码的你感到有点不安，不过这会让你在后面应用贝叶斯统计方法解决问题时容易一些。

本文包含以下主题：

• 统计模型；

• 概率及不确定性；

• 贝叶斯理论及统计推断；

• 单参数推断以及经典的抛硬币问题；

• 如何选择先验；

• 如何报告贝叶斯分析结果；

• 安装所有相关的Python库。

1.1　以建模为中心的统计学

统计学主要是收集、组织、分析并解释数据，因此，统计学的基础知识对数据分析来说至关重要。分析数据时一个非常有用的技巧是知道如何运用某种编程语言（如Python）编写代码。真实世界里充斥着复杂而杂乱的数据，因此对数据做一些预处理操作必不可少。即便你的数据已经是整理好的了，掌握一定的编程技巧仍然会给你带来很大帮助，因为如今的贝叶斯统计绝大多数都是计算统计学。

1.1.1　探索式数据分析

数据是统计学最基本的组成部分。数据的来源多，比如实验、计算机模拟、调查以及观测等。假如我们是数据生成或收集人员，首先要考虑的是要解决什么样的问题以及打算采用什么方法，然后再去着手准备数据。事实上，统计学有一个叫做实验设计的分支专门研究如何获取数据。在这个数据泛滥的年代，我们有时候会忘了获取数据并非总是很便宜。例如，尽管大型强子碰撞加速装置一天能产生上百TB的数据，但其建造却要花费数年的人力和智力。本文已经获取了数据并且数据是整理好的（这在现实中通常很少见），以便关注到本文的主题上来。

假设我们已经有了数据集，通常的做法是先对其探索并可视化，这样我们就能对手头的数据有个直观的认识。可以通过如下两步完成所谓的探索式数据分析过程：

• 描述性统计；

• 数据可视化。

其中，描述性统计是指如何用一些指标或统计值来定量地总结或刻画数据，例如你已经知道了如何用均值、众数、标准差、四分位差等指标来描述数据。数 据可视化是指用生动形象的方式表述数据，你大概对直方图、散点图等表现形式比较熟悉。乍看起来，探索式数据分析似乎是在复杂分析之前的一些准备工作，或者是作为一些复杂分析方法的替代品，不过探索式数据分析在理解、解释、检查、总结及交流贝叶斯分析结果等过程中依然有用。

1.1.2　统计推断

有时候，画画图、对数据做些简单的计算（比如求均值）就够了。另外一些时候，我们希望从数据中挖掘出一些更一般性的结论。我们可能希望了解数据是怎么生成的，也可能是想对未来还未观测到的数据做出预测，又或者是希望从多个对观测值的解释中找出最合理的一个，这些正是统计推断所做的事情。模型分为许多种，统计推断依赖的是概率模型，许多科学研究（以及我们对真实世界的认识）也都是基于模型的， 大脑不过是对现实进行建模的一台机器，可以观看相关的TED演讲了解大脑是如何对现实进行建模的，网址为http://www.tedxriodelaplata.org/videos/m%C3%A1quina-construye-realidad。

什么是模型？模型是对给定系统或过程的一种简化描述。这些描述只关注系统中某些重要的部分，因此，大多数模型的目的并不是解释整个系统。此外，假如我们有两个模型能用来解释同一份数据并且效果差不多，其中一个简单点，另一个复杂一些，通常我们倾向于更简单的模型，这称作奥卡姆剃刀，我们会在第6章模型比较部分讨论贝叶斯分析与其之间的联系。

不管你打算构建哪种模型，模型构建都遵循一些相似的基本准则，我们把贝叶斯模型的构建过程总结为如下3步。

（1）给定一些数据以及这些数据是如何生成的假设，然后构建模型。通常，这里的模型都是一些很粗略的近似，不过大多时候也够用了。

（2）利用贝叶斯理论将数据和模型结合起来，根据数据和假设推导出逻辑结论，我们称之为经数据拟合后的模型。

（3）根据多种标准，包括真实数据和对研究问题的先验知识，判断模型拟合得是否合理。

通常，我们会发现实际的建模过程并非严格按照该顺序进行的，有时候我们有可能跳到其中任何一步，原因可能是编写的程序出错了，也可能是找到了某种改进模型的方式，又或者是我们需要增加更多的数据。

贝叶斯模型是基于概率构建的，因此也称作概率模型。为什么基于概率呢？因为概率这个数学工具能够很好地描述数据中的不确定性，接下来我们将对其进行深入了解。

1.2　概率与不确定性

尽管概率论是数学中一个相当成熟和完善的分支，但关于概率的诠释仍然有不止一种。对于贝叶斯派而言，概率是对某一命题不确定性的衡量。假设我们对硬币一无所知，同时没有与抛硬币相关的任何数据，那么可以认为正面朝上的概率介于0到1之间，也就是说，在缺少信息的情况下，所有情况都是有可能发生的，此时不确定性也最大。假设现在我们知道硬币是公平的，那么我们可以认为正面朝上的概率是0.5或者是0.5附近的某个值（假如硬币不是绝对公平的话），如果此时收集数据，我们可以根据观测值进一步更新前面的先验假设，从而降低对该硬币偏差的不确定性。按照这种定义，提出以下问题都是自然而且合理的：火星上有多大可能存在生命？电子的质量是9.1×10⁻³¹kg的概率是多大？1816年7月9号是晴天的概率是多少？值得注意的是，类似火星上是否有生命这种问题的答案是二值化的，但我们关心的是，基于现有数据以及我们对火星物理条件和生物条件的了解，火星上存在生命的概率有多大。该命题取决于我们当前所掌握的信息而非客观的自然属性。我们使用概率是因为我们对事件不确定，而不代表事件本身是不确定的。由于这种概率的定义取决于我们的认知水平，有时也被称为概率的主观定义，这也就解释了为什么贝叶斯派总被称作主观统计。然而，这种定义并不是说所有命题都是同等有意义的，仅是承认我们对世界的理解是基于现有的数据和模型，是不完备的。不基于模型或理论去理解世界是不可能的。即使我们能脱离社会预设，最终也会受到生物上的限制：受进化过程影响，我们的大脑已经与世界上的模型建立了联系。我们注定要以人类的方式去思考，永远不可能像蝙蝠或其他动物那样思考。而且，宇宙是不确定的，总的来说我们能做的就是对其进行概率性描述。需要注意的是，不管世界的本原是确定的还是随机的，我们都将概率作为衡量不确定性的工具。

逻辑是指如何有效地推论，在亚里士多德学派或者经典的逻辑学中，一个命题只能是对或者错，而在贝叶斯学派定义的概率中，确定性只是概率上的一种特殊情况：一个正确命题的概率值为1，而一个错误命题的概率值为0。只有在我们拥有充分的数据表明火星上存在生物生长和繁殖时，我们才认为“火星上存在生命”这一命题为真的概率值为1。不过，需要注意的是，认定一个命题的概率值为0通常是比较困难的，这是因为火星上可能存在某些地方还没被探测到，或者是我们的实验有问题，又或者是某些其他原因导致我们错误地认为火星上没有生命而实际上有。与此相关的是克伦威尔准则（Cromwell’s Rule），其含义是指在对逻辑上正确或错误的命题赋予概率值时，应当避免使用0或者1。有意思的是，考克斯（Cox）在数学上证明了如果想在逻辑推理中加入不确定性，我们就必须使用概率论的知识，由此来说，贝叶斯定理可以视为概率论逻辑上的结果。因此，从另一个角度来看，贝叶斯统计是对逻辑学处理不确定性问题的一种扩充，当然这里毫无对主观推理的轻蔑。现在我们已经熟悉了贝叶斯学派对概率的理解，接下来就了解下概率相关的数学特性吧。如果你想深入学习概率论，可以参考阅读Joseph K Blitzstein和Jessica Hwang写的《概率导论》（Introduction to Probability）。

概率值介于[0,1]之间（包括0和1），其计算遵循一些法则，其中之一是乘法法则：

上式中，A和B同时发生的概率值等于B发生的概率值乘以在B发生的条件下A也发生的概率值，其中，表示A和B的联合概率， 表示条件概率，二者的现实意义是不同的，例如，路面是湿的概率跟下雨时候路面是湿的概率是不同的。条件概率可能比原来的概率高，也可能低。如果B并不能提供任何关于A的信息，那么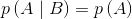， ，也就是说，A和B是相互独立的。相反，如果事件B能够给出关于事件A的一些信息，那么根据事件B提供的信息不同，事件A可能发生的概率会变得更高或是更低。

条件概率是统计学中的一个核心概念，接下来我们将看到，理解条件概率对于理解贝叶斯理论至关重要。这里我们换个角度来看条件概率，假如我们把前面的公式调整下顺序，就可以得到下面的公式：

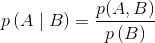
需要注意的是，我们不对0概率事件计算条件概率，因此，分母的取值范围是(0,1)，从而可以看出条件概率大于或等于联合概率。为什么要除以p(B)呢？因为在已经知道事件B发生的条件下，我们考虑的可能性空间就缩小到了事件B发生的范围内，然后将该范围内A发生的可能性除以B发生的可能性便得到了条件概率  。需要强调的是，所有的概率本质上都是条件概率，世间并没有绝对的概率。不管我们是否留意，在谈到概率时总是存在这样或那样的模型、假设或条件。比如，当我们讨论明天下雨的概率时，在地球上、火星上甚至宇宙中其他地方明天下雨的概率是不同的。同样，硬币正面朝上的概率取决于我们对硬币有偏性的假设。在理解概率的含义之后，接下来我们讨论另一个话题：概率分布。

1.2.1　概率分布

概率分布是数学中的一个概念，用来描述不同事件发生的可能性，通常这些事件限定在一个集合内，代表了所有可能发生的事件。在统计学里可以这么理解：数据是从某种参数未知的概率分布中生成的。由于并不知道具体的参数，我们只能借用贝叶斯定理从仅有的数据中反推参数。概率分布是构建贝叶斯模型的基础，不同分布组合在一起之后可以得到一些很有用的复杂模型。

本文会介绍一些概率分布，在第一次介绍某个概率分布时，我们会先花点时间理解它。最常见的一种概率分布是高斯分布，又叫正态分布，其数学公式描述如下：

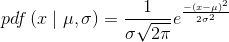
上式中，μ和σ是高斯分布的两个参数。第1个参数μ是该分布的均值（同时也是中位数和众数），其取值范围是任意实数，即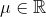 ；第2个参数σ是标准差，用来衡量分布的离散程度，其取值只能为正。由于μ和σ的取值范围无穷大，因此高斯分布的实例也有无穷多。虽然数学公式这一表达形式简洁明了，也有人称之有美感，不过得承认公式还是有些不够直观，我们可以尝试用Python代码将公式的含义重新表示出来。首先看看高斯分布都长什么样：

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns
mu_params = [-1, 0, 1]
sd_params = [0.5, 1, 1.5]
x = np.linspace(-7, 7, 100)
f, ax = plt.subplots(len(mu_params), len(sd_params), sharex=True, sharey=True)
for i in range(3):
    for j in range(3):
        mu = mu_params[i]
        sd = sd_params[j]
        y = stats.norm(mu, sd).pdf(x)
        ax[i,j].plot(x, y)
        ax[i,j].plot(0, 0, 
        label="$\\mu$ = {:3.2f}\n$\\sigma$ = {:3.2f}".format (mu, sd), alpha=0)
        ax[i,j].legend(fontsize=12)
ax[2,1].set_xlabel('$x$', fontsize=16)
ax[1,0].set_ylabel('$pdf(x)$', fontsize=16)
plt.tight_layout()

上面代码的输出结果如下：

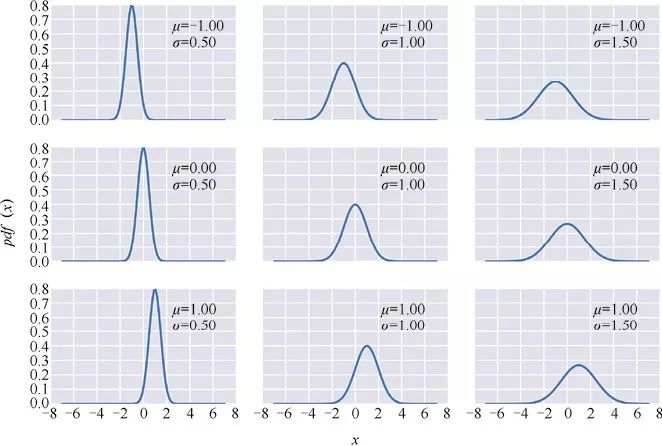
由概率分布生成的变量（例如x）称作随机变量，当然这并不是说该变量可以取任意值，相反，我们观测到该变量的数值受到概率分布的约束，而其随机性源于我们只知道变量的分布却无法准确预测该变量的值。通常，如果一个随机变量服从在参数μ和σ下的高斯分布，我们可以这样表示该变量：

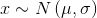
其中，符号～读作服从于某种分布。

随机变量分为两种：连续变量和离散变量。连续随机变量可以从某个区间内取任意值（我们可以用Python中的浮点型数据来表示），而离散随机变量只能取某些特定的值（我们可以用Python中的整型数据来表示）。

许多模型都假设，如果对服从于同一个分布的多个随机变量进行连续采样，那么各个变量的采样值之间相互独立，我们称这些随机变量是独立同分布的。用数学语言描述就是，如果两个随机变量x和y对于所有可能的取值都满足  ，那么称这两个变量相互独立。

时间序列是不满足独立同分布的一个典型例子。在时间序列中，需要对时间维度的变量多加留心。下面的例子是从http://cdiac.esd.ornl.gov中获取的数据。这份数据记录了从1959年到1997年大气中二氧化碳的含量。我们用以下代码将它写出来：

data = np.genfromtxt('mauna_loa_CO2.csv', delimiter=',')
plt.plot(data[:,0], data[:,1])
plt.xlabel('$year$', fontsize=16)
plt.ylabel('$CO_2 (ppmv)$', fontsize=16)

图中每个点表示每个月空气中二氧化碳含量的测量值，可以看到测量值是与时间相关的。我们可以观察到两个趋势：一个是季节性的波动趋势（这与植物周期性生长和衰败有关）；另一个是二氧化碳含量整体性的上升趋势。

1.2.2　贝叶斯定理与统计推断

到目前为止，我们已经学习了一些统计学中的基本概念和词汇，接下来让我们首先看看神奇的贝叶斯定理：

看起来稀松平常，似乎跟小学课本里的公式差不多，不过这就是关于贝叶斯统计你所需要掌握的全部。首先看看贝叶斯定理是怎么来的，这对我们理解它会很有帮助。事实上，我们已经掌握了如何推导它所需要的全部概率论知识。

• 根据前面提到的概率论中的乘法准则，我们有以下式子：

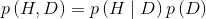
• 上式还可以写成如下形式：

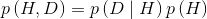
• 由于以上式子的左边相等，于是可以得到：

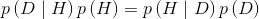
• 对上式调整下顺序，便得到了贝叶斯定理：

现在，让我们看看这个式子的含义及其重要性。首先，上式表明和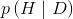并不一定相等，这一点非常重要，日常分析中即使系统学习过统计学和概率论的人也很容易忽略这点。我们举个简单例子来说明为什么二者不一定相等：有两条腿的动物就是人的概率和人有两条腿的概率显然是不同的。几乎所有人都有两条腿（除了某些人因为先天性原因或者意外导致没有两条腿），但是有两条腿的动物中很多都不是人类，比如鸟类。

在前面的式子中，如果我们将H理解为假设，D理解为数据，那么贝叶斯定理告诉我们的就是，在给定数据的条件下如何计算假设成立的概率。不过，如何把假设融入贝叶斯定理中去呢？答案是概率分布。换句话说，H是一种狭义上的假设，我们所做的实际上是寻找模型的参数（更准确地说是参数的分布）。因此，与其称H为假设，不如称之为模型，这样能避免歧义。

贝叶斯定理非常重要，后面会反复用到，这里我们先熟悉下其各个部分的名称：

• p(H )：先验；

• p(D | H )：似然；

• p(H | D)：后验；

• p(D)：证据。

先验分布反映的是在观测到数据之前我们对参数的了解，如果我们对参数一无所知（就跟《权力的游戏》中的雪诺一样），那么可以用一个不包含太多信息的均匀分布来表示。由于引入了先验，有些人会认为贝叶斯统计是偏主观的，然而，这些先验不过是构建模型时的一些假设罢了，其主观性跟似然差不多。

似然是指如何在实验分析中引入观测数据，反映的是在给定参数下得到某组观测数据的可信度。

后验分布是贝叶斯分析的结果，反映的是在给定数据和模型的条件下我们对问题的全部认知。需要注意，后验指的是我们模型中参数的概率分布而不是某个值，该分布正比于先验乘以似然。有这么个笑话：贝叶斯学派就像是这样一类人，心里隐约期待着一匹马，偶然间瞥见了一头驴，结果坚信他看到的是一头骡子。当然了，如果要刻意纠正这个笑话的话，在先验和似然都比较含糊的情况下，我们会得到一个（模糊的）“骡子”后验。不过，这个笑话也讲出了这样一个道理，后验其实是对先验和似然的某种折中。从概念上讲，后验可以看做是在观测到数据之后对先验的更新。事实上，一次分析中的后验，在收集到新的数据之后，也可以看做是下一次分析中的先验。这使得贝叶斯分析特别适合于序列化的数据分析，比如通过实时处理来自气象站和卫星的数据从而提前预警灾害，更详细的内容可以阅读在线机器学习方面的算法。

最后一个概念是证据，也称作边缘似然。正式地讲，证据是在模型的参数取遍所有可能值的条件下得到指定观测值的概率的平均。不过，本文的大部分内容并不关心这个概念，我们可以简单地把它当作归一化系数。我们只关心参数的相对值而非绝对值。把证据这一项忽略掉之后，贝叶斯定理可以表示成如下正比例形式：

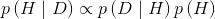
1.3　单参数推断

前面，我们学习了几个重要概念，其中有两个是贝叶斯统计的核心概念，这里我们用一句话再重新强调下：概率是用来衡量参数不确定性的，贝叶斯定理就是用来在观测到新的数据时正确更新这些概率以期降低我们的不确定性。

现在我们已经知道什么是贝叶斯统计了，接下来就从一个简单的例子入手，通过推断单个未知参数来学习如何进行贝叶斯统计。

1.3.1　抛硬币问题

抛硬币是统计学中的一个经典问题，其描述如下：我们随机抛一枚硬币，重复一定次数，记录正面朝上和反面朝上的次数，根据这些数据，我们需要回答诸如这枚硬币是否公平，以及更进一步这枚硬币有多不公平等问题。抛硬币是一个学习贝叶斯统计非常好的例子，一方面是因为几乎人人都熟悉抛硬币这一过程，另一方面是因为这个模型很简单，我们可以很容易计算并解决这个问题。此外，许多真实问题都包含两个互斥的结果，例如0或者1、正或者负、奇数或者偶数、垃圾邮件或者正常邮件、安全或者不安全、健康或者不健康等。因此，即便我们讨论的是硬币，该模型也同样适用于前面这些问题。

为了估计硬币的偏差，或者更广泛地说，想要用贝叶斯学派理论解决问题，我们需要数据和一个概率模型。对于抛硬币这个问题，假设我们已试验了一定次数并且记录了正面朝上的次数，也就是说数据部分已经准备好了，剩下的就是模型部分了。考虑到这是第一个模型，我们会列出所有必要的数学公式，并且一步一步推导。

通用模型

首先，我们要抽象出偏差的概念。我们称，如果一枚硬币总是正面朝上，那么它的偏差就是1，反之，如果总是反面朝上，那么它的偏差就是0，如果正面朝上和反面朝上的次数各占一半，那么它的偏差就是0.5。这里用参数θ来表示偏差，用y表示N次抛硬币实验中正面朝上的次数。根据贝叶斯定理，我们有如下公式：

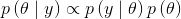
这里需要指定我们将要使用的先验和似然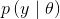分别是什么。让我们首先从似然开始。

选择似然

假设多次抛硬币的结果相互之间没有影响，也就是说每次抛硬币都是相互独立的，同时还假设结果只有两种可能：正面朝上或者反面朝上。但愿你能认同我们对这个问题做出的合理假设。基于这些假设，一个不错的似然候选是二项分布：

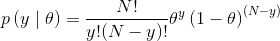
这是一个离散分布，表示N次抛硬币实验中y次正面朝上的概率（或者更通俗地描述是，N次实验中，y次成功的概率）。下面的代码生成了9个二项分布，每个子图中的标签显示了对应的参数：

n_params = [1, 2, 4]
p_params = [0.25, 0.5, 0.75]
x = np.arange(0, max(n_params)+1)
f, ax = plt.subplots(len(n_params), len(p_params), sharex=True, sharey=True)
for i in range(3):
    for j in range(3):
        n = n_params[i]
        p = p_params[j]
        y = stats.binom(n=n, p=p).pmf(x)
        ax[i,j].vlines(x, 0, y, colors='b', lw=5)
        ax[i,j].set_ylim(0, 1)
        ax[i,j].plot(0, 0, label="n = {:3.2f}\np = 
         {:3.2f}".format(n, p), alpha=0)
        ax[i,j].legend(fontsize=12)
ax[2,1].set_xlabel('$\\theta$', fontsize=14)
ax[1,0].set_ylabel('$p(y|\\theta)$', fontsize=14)
ax[0,0].set_xticks(x)

二项分布是似然的一个合理选择，直观上讲，θ可以看作抛一次硬币时正面朝上的可能性，并且该过程发生了y次。类似地，我们可以把“1−θ”看作抛一次硬币时反面朝上的概率，并且该过程发生了“N−y”次。

假如我们知道了θ，那么就可以从二项分布得出硬币正面朝上的分布。如果我们不知道θ，也别灰心，在贝叶斯统计中，当我们不知道某个参数的时候，就对其赋予一个先验。接下来继续选择先验。

选择先验

这里我们选用贝叶斯统计中最常见的beta分布，作为先验，其数学形式如下：

仔细观察上面的式子可以看出，除了Γ部分之外，beta分布和二项分布看起来很像。Γ是希腊字母中大写的伽马，用来表示伽马函数。现在我们只需要知道，用分数表示的第一项是一个正则化常量，用来保证该分布的积分为1，此外，和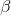两个参数用来控制具体的分布形态。beta分布是我们到目前为止见到的第3个分布，利用下面的代码，我们可以深入了解其形态：

params = [0.5, 1, 2, 3]
x = np.linspace(0, 1, 100)
f, ax = plt.subplots(len(params), len(params), sharex=True, sharey=True)
for i in range(4):
    for j in range(4):
        a = params[i]
        b = params[j]
        y = stats.beta(a, b).pdf(x)
        ax[i,j].plot(x, y)
      ax[i,j].plot(0, 0, label="$\\alpha$ = {:3.2f}\n$\\beta$ = {:3.2f}".format(a, b), alpha=0)
        ax[i,j].legend(fontsize=12)
ax[3,0].set_xlabel('$\\theta$', fontsize=14)
ax[0,0].set_ylabel('$p(\\theta)$', fontsize=14)
plt.savefig('B04958_01_04.png', dpi=300, figsize=(5.5, 5.5))

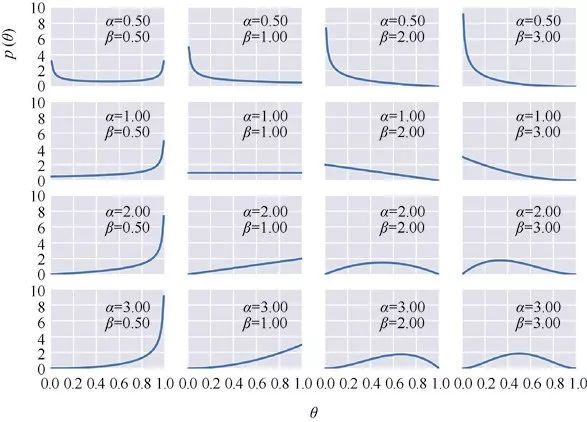
为什么要在模型中使用beta分布呢？在抛硬币以及一些其他问题中使用beta分布的原因之一是：beta分布的范围限制在0到1之间，这跟我们的参数一样；另一个原因是其通用性，从前面的图可以看出，该分布可以有多种形状，包括均匀分布、类高斯分布、U型分布等。第3个原因是：beta分布是二项分布（前面我们使用了该分布描述似然）的共轭先验。似然的共轭先验是指，将该先验分布与似然组合在一起之后，得到的后验分布与先验分布的表达式形式仍然是一样的。简单说，就是每次用beta分布作为先验、二项分布作为似然时，我们会得到一个beta分布的后验。除beta分布之外还有许多其他共轭先验，例如高斯分布，其共轭先验就是自己。关于共轭先验更详细的内容可以查看https://en.wikipedia.org/wiki/Conjugate_prior。许多年来，贝叶斯分析都限制在共轭先验范围内，这主要是因为共轭能让后验在数学上变得更容易处理，要知道贝叶斯统计中一个常见问题的后验都很难从分析的角度去解决。在建立合适的计算方法来解决任意后验之前，这只是个折中的办法。

计算后验

首先回忆一下贝叶斯定理：后验正比于似然乘以先验。

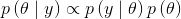
对于我们的问题而言，需要将二项分布乘以beta分布：

现在，对上式进行简化。针对我们的实际问题，可以先把与θ不相关的项去掉而不影响结果，于是得到下式：

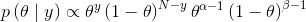
重新整理之后得到：

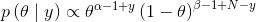
可以看出，上式和beta分布的形式很像（除了归一化部分），其对应的参数分别为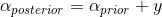 、。也就是说，在抛硬币这个问题中，后验分布是如下beta分布：

计算后验并画图
现在已经有了后验的表达式，我们可以用Python对其计算并画出结果。下面的代码中，其实只有一行是用来计算后验结果的，其余的代码都是用来画图的：

theta_real = 0.35
trials = [0, 1, 2, 3, 4, 8, 16, 32, 50, 150]
data = [0, 1, 1, 1, 1, 4, 6, 9, 13, 48]
beta_params = [(1, 1), (0.5, 0.5), (20, 20)]
dist = stats.beta
x = np.linspace(0, 1, 100)
for idx, N in enumerate(trials):
    if idx == 0:
        plt.subplot(4,3, 2)
    else:
        plt.subplot(4,3, idx+3)
    y = data[idx]
    for (a_prior, b_prior), c in zip(beta_params, ('b', 'r', 'g')):
        p_theta_given_y = dist.pdf(x, a_prior + y, b_prior + N - y)
        plt.plot(x, p_theta_given_y, c)
        plt.fill_between(x, 0, p_theta_given_y, color=c, alpha=0.6)
    plt.axvline(theta_real, ymax=0.3, color='k')
    plt.plot(0, 0, label="{:d} experiments\n{:d} heads".format(N, y), alpha=0)
    plt.xlim(0,1)
    plt.ylim(0,12)
    plt.xlabel(r"$\theta$") 
    plt.legend()
    plt.gca().axes.get_yaxis().set_visible(False)
plt.tight_layout()
plt.savefig('B04958_01_05.png', dpi=300, figsize=(5.5, 5.5))

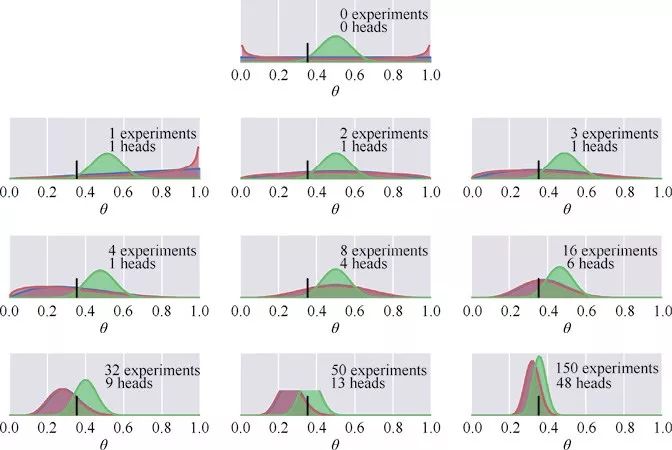
在上图的第一行中，实验的次数为0，因此第一个图中的曲线描绘的是先验分布，其中有3条曲线，每条曲线分别表示一种先验。

• 蓝色的线是一个均匀分布先验，其含义是：偏差的所有可能取值都是等概率的。

• 红色的线与均匀分布有点类似，对抛硬币这个例子而言可以理解为：偏差等于0或者1的概率要比其他值更大一些。

• 最后一条绿色的线集中在中间值0.5附近，该分布反映了通常硬币正面朝上和反面朝上的概率大致是差不多的。我们也可以称，该先验与大多数硬币都是公平的这一信念是兼容的。“兼容”这个词在贝叶斯相关的讨论中会经常用到，特别是在提及受到数据启发的模型时。

剩余的子图描绘了后续实验的后验分布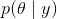，回想一下，后验可以看做是在给定数据之后更新了的先验。实验（抛硬币）的次数和正面朝上的次数分别标注在每个子图中。此外每个子图中在横轴0.35附近还有一个黑色的竖线，表示的是真实的θ，显然，在真实情况下，我们并不知道该值，在这里标识出来只是为了方便理解。从这幅图中可以学到很多贝叶斯分析方面的知识。

• 贝叶斯分析的结果是后验分布而不是某个值，该分布描述了根据给定数据和模型得到的不同数值的可能性。

• 后验最可能的值是根据后验分布的形态决定的（也就是后验分布的峰值）。

• 后验分布的离散程度与我们对参数的不确定性相关；分布越离散，不确定性越大。

• 尽管1/2=4/8=0.5，但从图中可以看出，前者的不确定性要比后者大。这是因为我们有了更多的数据来支撑我们的推断，该直觉也同时反映在了后验分布上。

• 在给定足够多的数据时，两个或多个不同先验的贝叶斯模型会趋近于收敛到相同的结果。在极限情况下，如果有无限多的数据，不论我们使用的是怎样的先验，最终都会得到相同的后验。注意这里说的无限多是指某种程度而非某个具体的数量，也就是说，从实际的角度来讲，某些情况下无限多的数据可以通过比较少量的数据近似。

• 不同后验收敛到相同分布的速度取决于数据和模型。从前面的图中可以看出，蓝色和红色的后验在经过8次实验之后就很难看出区别了，而红色的曲线则一直到150次实验之后才与另外两个后验看起来比较接近。

• 有一点从前面的图中不太容易看出来，如果我们一步一步地更新后验，最后得到的结果跟一次性计算得到的结果是一样的。换句话说，我们可以对后验分150次计算，每次增加一个新的观测数据并将得到的后验作为下一次计算的先验，也可以在得到150次抛硬币的结果之后一次性计算出后验，而这两种计算方式得到的结果是完全一样的。这个特点非常有意义，在许多数据分析的问题中，每当我们得到新的数据时可以更新估计值。

先验的影响以及如何选择合适的先验

从前面的例子可以看出，先验对分析的结果会有影响。一些贝叶斯分析的新手（以及一些诋毁该方法的人）会对如何选择先验感到茫然，因为他们不希望先验起到决定性作用，而是更希望数据本身替自己说话！有这样的想法很正常，不过我们得牢记，数据并不会真的“说话”，只有在模型中才会有意义，包括数学上的和脑海中的模型。面对同一主题下的同一份数据，不同人会有不同的看法，这类例子在科学史上有许多，查看以下链接可以了解《纽约时报》最近一次实验的例子：http://www.nytimes.com/interactive/2016/09/20/upshot/the-error-the-polling-world-rarely-talks-about.html?_r=0。

有些人青睐于使用没有信息量的先验（也称作均匀的、含糊的或者发散的先验），这类先验对分析过程的影响最小。本文将遵循Gelman、McElreath和Kruschke 3人的建议^[1]，更倾向于使用带有较弱信息量的先验。在许多问题中，我们对参数可以取的值一般都会有些了解，比如，参数只能是正数，或者知道参数近似的取值范围，又或者是希望该值接近0或大于/小于某值。这种情况下，我们可以给模型加入一些微弱的先验信息而不必担心该先验会掩盖数据本身的信息。由于这类先验会让后验近似位于某一合理的边界内，因此也被称作正则化先验。

当然，使用带有较多信息量的强先验也是可行的。视具体的问题不同，有可能很容易或者很难找到这类先验，例如在我工作的领域（结构生物信息学），人们会尽可能地利用先验信息，通过贝叶斯或者非贝叶斯的方式来了解和预测蛋白质的结构。这样做是合理的，原因是我们在数十年间已经从上千次精心设计的实验中收集了数据，因而有大量可信的先验信息可供使用。如果你有可信的先验信息，完全没有理由不去使用。试想一下，如果一个汽车工程师每次设计新车的时候，他都要重新发明内燃机、轮子乃至整个汽车，这显然不是正确的方式。

现在我们知道了先验有许多种，不过这并不能缓解我们选择先验时的焦虑。或许，最好是没有先验，这样事情就简单了。不过，不论是否基于贝叶斯，模型都在某种程度上拥有先验，即使这里的先验并没有明确表示出来。事实上，许多频率统计学方面的结果可以看做是贝叶斯模型在一定条件下的特例，比如均匀先验。让我们再仔细看看前面那幅图，可以看到蓝色后验分布的峰值与频率学分析中θ的期望值是一致的：

注意，这里是点估计而不是后验分布（或者其他类型的分布）。由此看出，你没办法完全避免先验，不过如果你在分析中引入先验，得到的会是概率分布分布而不只是最可能的一个值。明确引入先验的另一个好处是，我们会得到更透明的模型，这意味着更容易评判、（广义上的）调试以及优化。构建模型是一个循序渐进的过程，有时候可能只需要几分钟，有时候则可能需要数年；有时候整个过程可能只有你自己，有时候则可能包含你不认识的人。而且，模型复现很重要，而模型中透明的假设能有助于复现。

在特定分析任务中，如果我们对某个先验或者似然不确定，可以自由使用多个先验或者似然进行尝试。模型构建过程中的一个环节就是质疑假设，而先验就是质疑的对象之一。不同的假设会得到不同的模型，根据数据和与问题相关的领域知识，我们可以对这些模型进行比较。

由于先验是贝叶斯统计中的一个核心内容，在接下来遇到新的问题时我们还会反复讨论它，因此，如果你对前面的讨论内容感到有些疑惑，别太担心，要知道人们在这个问题上已经困惑了数十年并且相关的讨论一直在继续。

1.3.2　报告贝叶斯分析结果

现在我们已经有了后验，相关的分析也就结束了。下面我们可能还需要对分析结果进行总结，将分析结果与别人分享，或者记录下来以备日后使用。

1.3.3　模型注释和可视化

根据受众不同，你可能在交流分析结果的同时还需要交流模型。以下是一种简单表示概率模型的常见方式：

这是我们抛硬币例子中用到的模型。符号～表示左边随机变量的分布服从右边的分布形式，也就是说，这里θ服从于参数为α和β的Beta分布，而y服从于参数为n = 1和p = θ的二项分布。该模型还可以用类似Kruschke文中的图表示成如下形式：

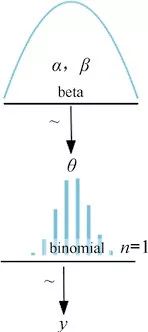
在第一层，根据先验生成了θ，然后通过似然生成最下面的数据。图中的箭头表示变量之间的依赖关系，符号～表示变量的随机性。

本书中用到的类似Kruschke中的图都是由Rasmus Bååth（http://www.sumsar.net/blog/2013/10/diy-kruschke-style-diagrams/）提供的模板生成的。

1.3.4　总结后验

贝叶斯分析的结果是后验分布，该分布包含了有关参数在给定数据和模型下的所有信息。如果可能的话，我们只需要将后验分布展示给观众即可。通常，一个不错的做法是：同时给出后验分布的均值（或者众数、中位数），这样能让我们了解该分布的中心，此外还可以给出一些描述该分布的衡量指标，如标准差，这样人们能对我们估计的离散程度和不确定性有一个大致的了解。拿标准差衡量类似正态分布的后验分布很合适，不过对于一些其他类型的分布（如偏态分布）却可能得出误导性结论，因此，我们还可以采用下面的方式衡量。

最大后验密度

一个经常用来描述后验分布分散程度的概念是最大后验密度（ Highest Posterior Density，HPD）区间。一个HPD区间是指包含一定比例概率密度的最小区间，最常见的比例是95%HPD或98%HPD，通常还伴随着一个50%HPD。如果我们说某个分析的HPD区间是[2, 5]，其含义是指：根据我们的模型和数据，参数位于2～5的概率是0.95。这是一个非常直观的解释，以至于人们经常会将频率学中的置信区间与贝叶斯方法中的可信区间弄混淆。如果你对频率学的范式比较熟悉，请注意这两种区间的区别。贝叶斯学派的分析告诉我们的是参数取值的概率，这在频率学的框架中是不可能的，因为频率学中的参数是固定值，频率学中的置信区间只能包含或不包含参数的真实值。在继续深入之前，有一点需要注意：选择95%还是50%或者其他什么值作为HPD区间的概率密度比例并没有什么特殊的地方，这些不过是经常使用的值罢了。比如，我们完全可以选用比例为91.37%的HPD区间。如果你选的是95%，这完全没问题，只是要记住这只是个默认值，究竟选择多大比例仍然需要具体问题具体分析。

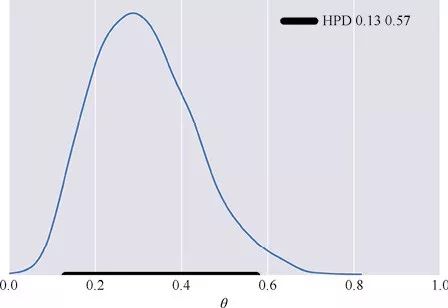
对单峰分布计算95%HPD很简单，只需要计算出2.5%和97.5%处的值即可：

def naive_hpd(post):
    sns.kdeplot(post)
    HPD = np.percentile(post, [2.5, 97.5])
    plt.plot(HPD, [0, 0], label='HPD {:.2f} {:.2f}'.format(*HPD), 
      linewidth=8, color='k')
    plt.legend(fontsize=16);
    plt.xlabel(r'$\theta$', fontsize=14)
    plt.gca().axes.get_yaxis().set_ticks([])
np.random.seed(1)
post = stats.beta.rvs(5, 11, size=1000)
naive_hpd(post)
plt.xlim(0, 1)

对于多峰分布而言，计算HPD要稍微复杂些。如果把对HPD的原始定义应用到混合高斯分布上，我们可以得到：

np.random.seed(1)
gauss_a = stats.norm.rvs(loc=4, scale=0.9, size=3000)
gauss_b = stats.norm.rvs(loc=-2, scale=1, size=2000)
mix_norm = np.concatenate((gauss_a, gauss_b))
naive_hpd(mix_norm)
plt.savefig('B04958_01_08.png', dpi=300, figsize=(5.5, 5.5))

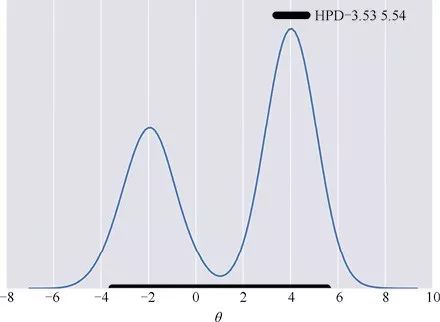
从上图可以看出，通过原始HPD定义计算出的可信区间包含了一部分概率较低的区间，位于[0,2]。为了正确计算出HPD，这里我们使用了plot_post函数，你可以从本书附带的代码中下载对应的源码：

from plot_post import plot_post
plot_post(mix_norm, roundto=2, alpha=0.05)
plt.legend(loc=0, fontsize=16)
plt.xlabel(r"$\theta$", fontsize=14)

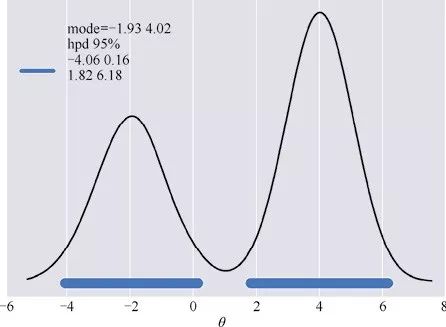
从上图可以看出，95%HPD包含两个区间，同时plot_post函数也返回了两个众数。

1.4　后验预测检查

贝叶斯方法的一个优势是：一旦得到了后验分布，我们可以根据该后验生成未来的数据y，即用来做预测。后验预测检查主要是对观测数据和预测数据进行比较从而发现这两个集合的不同之处，其目的是进行一致性检查。生成的数据和观测的数据应该看起来差不多，否则有可能是建模出现了问题或者输入数据到模型时出了问题，不过就算我们没有出错，两个集合仍然有可能出现不同。尝试去理解其中的偏差有助于我们改进模型，或者至少能知道我们模型的极限。即使我们并不知道如何去改进模型，但是理解模型捕捉到了问题或数据的哪些方面以及没能捕捉到哪些方面也是非常有用的信息。也许模型能够很好地捕捉到数据中的均值但却没法预测出罕见值，这可能是个问题，不过如果我们只关心均值，这个模型对我们而言也还是可用的。通常我们的目的不是去声称一个模型是错误的，我们更愿意遵循George Box的建议，即所有模型都是错的，但某些是有用的。我们只想知道模型的哪个部分是值得信任的，并测试该模型是否在特定方面符合我们的预期。不同学科对模型的信任程度显然是不同的，物理学中研究的系统是在高可控条件下依据高深理论运行的，因而模型可以看做是对现实的不错描述，而在一些其他学科如社会学和生物学中，研究的是错综复杂的孤立系统，因而模型对系统的认知较弱。尽管如此，不论你研究的是哪一门学科，都需要对模型进行检查，利用后验预测和本文学到的探索式数据分析中的方法去检查模型。

1.5　安装必要的Python库

本书用到的代码是用Python 3.5写的，建议使用Python 3的最新版本运行，尽管大多数代码也能在更老的Python版本（包括Python 2.7）上运行，不过可能会需要做些微调。

本书建议使用Anaconda安装Python及相关库，Anaconda是一个用于科学计算的软件分发，你可以从以下链接下载并了解更多：https://www.continuum.io/downloads。在系统上装好Anaconda之后，就可以通过以下方式安装Python库了：

conda install NamePackage

我们会用到以下Python库：

• Ipython 5.0；

• NumPy 1.11.1；

• SciPy 0.18.1；

• Pandas 0.18.1；

• Matplotlib 1.5.3；

• Seaborn 0.7.1；

• PyMC3 3.0。

在命令行中执行以下命令即可安装最新稳定版的PyMC3：

pip install pymc3

1.6　总结

我们的贝叶斯之旅首先围绕统计建模、概率论和贝叶斯定理做了一些简短讨论，然后用抛硬币的例子介绍了贝叶斯建模和数据分析，借用这个经典例子传达了贝叶斯统计中的一些最重要的思想，比如用概率分布构建模型并用概率分布来表示不确定性。此外我们尝试揭示了如何选择先验，并将其与数据分析中的一些其他问题置于同等地位（怎么选择似然，为什么要解决该问题等）。本文的最后讨论了如何解释和报告贝叶斯分析的结果。本文我们对贝叶斯分析的一些主要方面做了简要总结，后面还会重新回顾这些内容，从而充分理解和吸收，并为后面理解更高级的内容打下基础。下面我们会重点关注一些构建和分析更复杂模型的技巧，此外，还会介绍PyMC3并将其用于实现和分析贝叶斯模型。

推荐阅读
决策树可视化，被惊艳到了！
开发机器学习APP，太简单了
周志华教授：关于深度学习的一点思考
200 道经典机器学习面试题总结
卷积神经网络（CNN）数学原理解析
收手吧，华强！我用机器学习帮你挑西瓜

如有收获，欢迎三连👇