基于Msnhnet实现最优化问题(上)SGD&&牛顿法
共 8691字，需浏览 18分钟
·
2021-07-05 04:15
使用Msnhnet实现最优化问题(1)一(无约束优化问题)
1. 预备知识
范数
范数
范数
范数之间的关系
梯度、Jacobian矩阵和Hessian矩阵
1.梯度: f(x)多元标量函数一阶连续可微
2.Jacobian矩阵: f(x)多元向量函数一阶连续可微
3.Hessian矩阵: f(x)二阶连续可微
注: 二次函数,其中对称矩阵则：
Taylor公式
如果在处是一阶连续可微，令,则其Maclaurin余项的一阶Taylor展开式为L:
如果在处是二阶连续可微，令,则其Maclaurin余项的二阶Taylor展开式为:
或者:
2. 凸函数判别准则
一阶判别定理
设在开凸集内函数一阶可微有
1.f(x)在凸集F上为凸函数,则对于任意 ,有:
2.f(x)在凸集F上为严格凸函数,则对于任意有
二阶判别定理
设在开凸集内函数二阶可微,有:
1.f(x)在凸集F上为凸函数,则对于任意,Hessian矩阵半正定
2.f(x)在凸集F上为严格凸函数,则对于,Hessian矩阵正定
矩阵正定判定
1.若所有特征值均大于零，则称为正定
2.若所有特征值均大于等于零，则称为半正定
3. 无约束优化
无约束优化基本架构
step1.给定初始点, k=0以及最小误差
step2.判断是否满足终止条件，是则终止
step3.确定f(x)在点x_k的下降方向
step4.确定下降步长, , 计算，满足
step5.令 ; 返回step2
终止条件:
4. 梯度下降法
在梯度下降算法中被称作为学习率或者步长;梯度的方向
梯度下降不一定能够找到全局最优解，有可能是局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。
判断是否满足终止条件，是则终止
举例
#include <Msnhnet/math/MsnhMatrixS.h>
#include <Msnhnet/cv/MsnhCVGui.h>
#include <iostream>
using namespace Msnhnet;
class SteepestDescent
{
public:
SteepestDescent(double learningRate, int maxIter, double eps):_learningRate(learningRate),_maxIter(maxIter),_eps(eps){}
void setLearningRate(double learningRate)
{
_learningRate = learningRate;
}
void setMaxIter(int maxIter)
{
_maxIter = maxIter;
}
virtual int solve(MatSDS &startPoint) = 0;
void setEps(double eps)
{
_eps = eps;
}
const std::vector<Vec2F32> &getXStep() const
{
return _xStep;
}
protected:
double _learningRate = 0;
int _maxIter = 100;
double _eps = 0.00001;
std::vector<Vec2F32> _xStep;
protected:
virtual MatSDS calGradient(const MatSDS& point) = 0;
virtual MatSDS function(const MatSDS& point) = 0;
};
class NewtonProblem1:public SteepestDescent
{
public:
NewtonProblem1(double learningRate, int maxIter, double eps):SteepestDescent(learningRate, maxIter, eps){}
MatSDS calGradient(const MatSDS &point) override
{
MatSDS dk(1,2);
// df(x) = (2x_1,2x_2)^T
double x1 = point(0,0);
double x2 = point(0,1);
dk(0,0) = 6*x1 - 2*x1*x2;
dk(0,1) = 6*x2 - x1*x1;
dk = -1*dk;
return dk;
}
MatSDS function(const MatSDS &point) override
{
MatSDS f(1,1);
double x1 = point(0,0);
double x2 = point(0,1);
f(0,0) = 3*x1*x1 + 3*x2*x2 - x1*x1*x2;
return f;
}
int solve(MatSDS &startPoint) override
{
MatSDS x = startPoint;
for (int i = 0; i < _maxIter; ++i)
{
_xStep.push_back({(float)x[0],(float)x[1]});
MatSDS dk = calGradient(x);
std::cout<<std::left<<"Iter(s): "<<std::setw(4)<<i<<", Loss: "<<std::setw(12)<<dk.L2()<<" Result: "<<function(x)[0]<<std::endl;
if(dk.L2() < _eps)
{
startPoint = x;
return i+1;
}
x = x + _learningRate*dk;
}
return -1;
}
};
int main()
{
NewtonProblem1 function(0.1, 100, 0.001);
MatSDS startPoint(1,2,{1.5,1.5});
int res = function.solve(startPoint);
if(res < 0)
{
std::cout<<"求解失败"<<std::endl;
}
else
{
std::cout<<"求解成功! 迭代次数: "<<res<<std::endl;
std::cout<<"最小值点："<<res<<std::endl;
startPoint.print();
std::cout<<"此时方程的值为："<<std::endl;
function.function(startPoint).print();
#ifdef WIN32
Gui::setFont("c:/windows/fonts/MSYH.TTC",16);
#endif
std::cout<<"按\"esc\"退出!"<<std::endl;
Gui::plotLine(u8"最速梯度下降法迭代X中间值","x",function.getXStep());
Gui::wait();
}
}
结果:迭代次数13次，求得最小值点
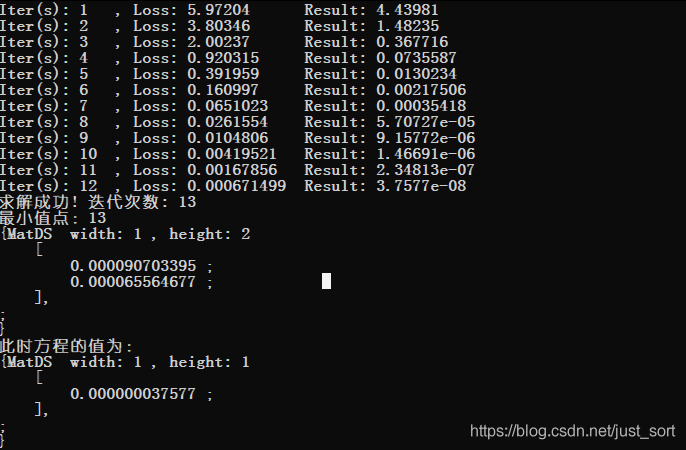迭代次数13次，求得最小值点
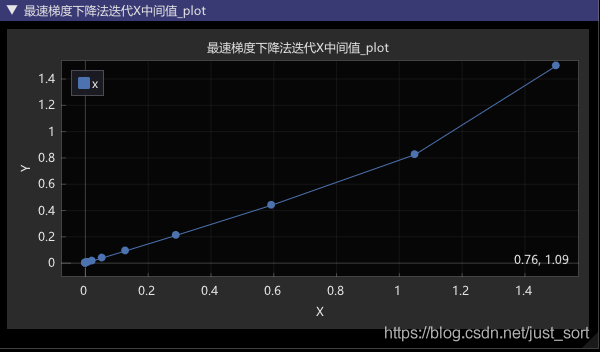SGD迭代过程中对X进行可视化4. 牛顿法
梯度下降法初始点选取问题, 会导致迭代次数过多, 可使用牛顿法可以处理.
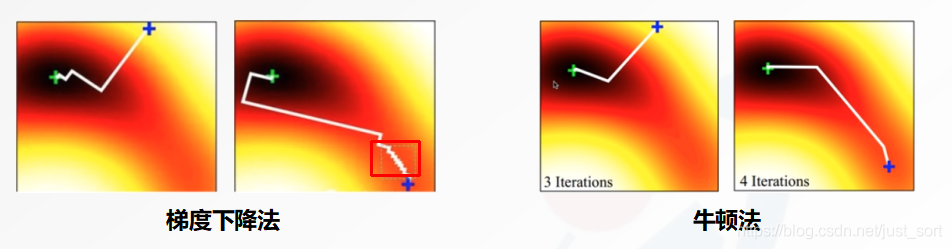牛顿法和SGD可视化比较目标函数在处进行二阶泰勒展开:
目标函数变为:
关于求导,并让其为0,可以得到步长:
与梯度下降法比较，牛顿法的好处：
A点的Jacobian和B点的Jacobian值差不多, 但是A点的Hessian矩阵较大, 步长比较小, B点的Hessian矩阵较小,步长较大, 这个是比较合理的.如果是梯度下降法,则梯度相同, 步长也一样,很显然牛顿法要好得多. 弊端就是Hessian矩阵计算量非常大.
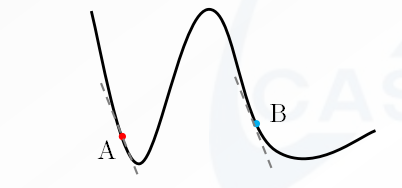牛顿法和梯度下降法的优缺点步骤
step1.给定初始点, ,学习率和最小误差
step2.判断是否满足终止条件，是则终止
step3.确定在点的下降方向
step4.令 返回step2
举例
#include <Msnhnet/math/MsnhMatrixS.h>
#include <iostream>
#include <Msnhnet/cv/MsnhCVGui.h>
using namespace Msnhnet;
class Newton
{
public:
Newton(int maxIter, double eps):_maxIter(maxIter),_eps(eps){}
void setMaxIter(int maxIter)
{
_maxIter = maxIter;
}
virtual int solve(MatSDS &startPoint) = 0;
void setEps(double eps)
{
_eps = eps;
}
//正定性判定
bool isPosMat(const MatSDS &H)
{
MatSDS eigen = H.eigen()[0];
for (int i = 0; i < eigen.mWidth; ++i)
{
if(eigen[i]<=0)
{
return false;
}
}
return true;
}
const std::vector<Vec2F32> &getXStep() const
{
return _xStep;
}
protected:
int _maxIter = 100;
double _eps = 0.00001;
std::vector<Vec2F32> _xStep;
protected:
virtual MatSDS calGradient(const MatSDS& point) = 0;
virtual MatSDS calHessian(const MatSDS& point) = 0;
virtual bool calDk(const MatSDS& point, MatSDS &dk) = 0;
virtual MatSDS function(const MatSDS& point) = 0;
};
class NewtonProblem1:public Newton
{
public:
NewtonProblem1(int maxIter, double eps):Newton(maxIter, eps){}
MatSDS calGradient(const MatSDS &point) override
{
MatSDS J(1,2);
double x1 = point(0,0);
double x2 = point(0,1);
J(0,0) = 6*x1 - 2*x1*x2;
J(0,1) = 6*x2 - x1*x1;
return J;
}
MatSDS calHessian(const MatSDS &point) override
{
MatSDS H(2,2);
double x1 = point(0,0);
double x2 = point(0,1);
H(0,0) = 6 - 2*x2;
H(0,1) = -2*x1;
H(1,0) = -2*x1;
H(1,1) = 6;
return H;
}
bool calDk(const MatSDS& point, MatSDS &dk) override
{
MatSDS J = calGradient(point);
MatSDS H = calHessian(point);
if(!isPosMat(H))
{
return false;
}
dk = -1*H.invert()*J;
return true;
}
MatSDS function(const MatSDS &point) override
{
MatSDS f(1,1);
double x1 = point(0,0);
double x2 = point(0,1);
f(0,0) = 3*x1*x1 + 3*x2*x2 - x1*x1*x2;
return f;
}
int solve(MatSDS &startPoint) override
{
MatSDS x = startPoint;
for (int i = 0; i < _maxIter; ++i)
{
_xStep.push_back({(float)x[0],(float)x[1]});
MatSDS dk;
bool ok = calDk(x, dk);
if(!ok)
{
return -2;
}
x = x + dk;
std::cout<<std::left<<"Iter(s): "<<std::setw(4)<<i<<", Loss: "<<std::setw(12)<<dk.L2()<<" Result: "<<function(x)[0]<<std::endl;
if(dk.LInf() < _eps)
{
startPoint = x;
return i+1;
}
}
return -1;
}
};
int main()
{
NewtonProblem1 function(100, 0.01);
MatSDS startPoint(1,2,{1.5,1.5});
try
{
int res = function.solve(startPoint);
if(res == -1)
{
std::cout<<"求解失败"<<std::endl;
}
else if(res == -2)
{
std::cout<<"Hessian 矩阵非正定, 求解失败"<<std::endl;
}
else
{
std::cout<<"求解成功! 迭代次数: "<<res<<std::endl;
std::cout<<"最小值点："<<res<<std::endl;
startPoint.print();
std::cout<<"此时方程的值为："<<std::endl;
function.function(startPoint).print();
#ifdef WIN32
Gui::setFont("c:/windows/fonts/MSYH.TTC",16);
#endif
std::cout<<"按\"esc\"退出!"<<std::endl;
Gui::plotLine(u8"牛顿法迭代X中间值","x",function.getXStep());
Gui::wait();
}
}
catch(Exception ex)
{
std::cout<<ex.what();
}
}
结果:对于初始点 (1.5,1.5) 迭代次数6次，求得最小值点,迭代次数比梯度下降法少了一半
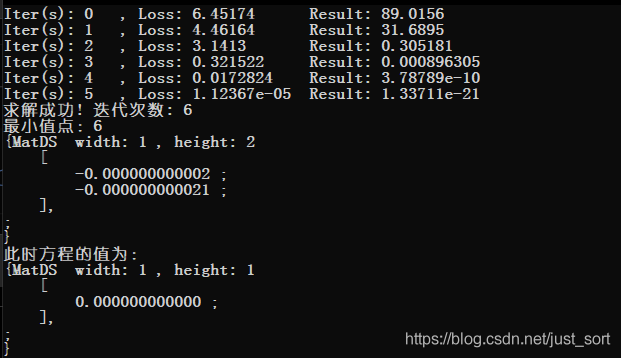牛顿法求解最小值，只需要迭代六次
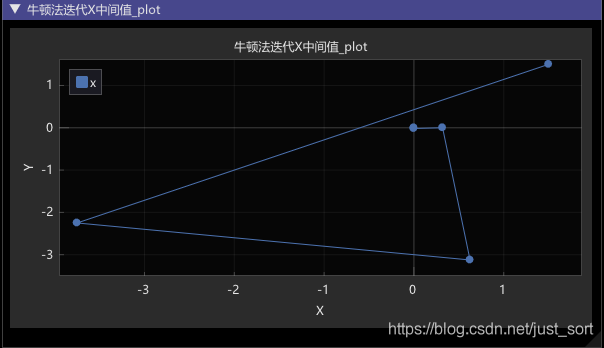牛顿法迭代过程中，X的可视化结果，可以看到这里X迈的步子是很大的结果:二对于初始点 (0,3), 由于在求解过程中会出现hessian矩阵非正定的情况，故需要对newton法进行改进.（这个请看下期文章）
求解失败5. 源码
https://github.com/msnh2012/numerical-optimizaiton(https://github.com/msnh2012/numerical-optimizaiton)
6. 依赖包
https://github.com/msnh2012/Msnhnet(https://github.com/msnh2012/Msnhnet)
7. 参考文献
- Numerical Optimization. Jorge Nocedal Stephen J. Wrigh
- Methods for non-linear least squares problems. K. Madsen, H.B. Nielsen, O. Tingleff.
- Practical Optimization_ Algorithms and Engineering Applications. Andreas Antoniou Wu-Sheng Lu
- 最优化理论与算法. 陈宝林
- 数值最优化方法. 高立
网盘资料下载：链接：https://pan.baidu.com/s/1hpFwtwbez4mgT3ccJp33kQ 提取码：b6gq
8. 最后
- 欢迎关注我们维护的一个深度学习框架Msnhnet:
- https://github.com/msnh2012/Msnhnet Msnhnet除了是一个深度网络推理库之外，还是一个小型矩阵库，包含了矩阵常规操作，LU分解，Cholesky分解，SVD分解。
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：
二维码