手把手,74行代码实现手写数字识别
日期 :2021年08月29日
正文共 :7361字
龙心尘和寒小阳:从事机器学习/数据挖掘相关应用工作,热爱机器学习/数据挖掘


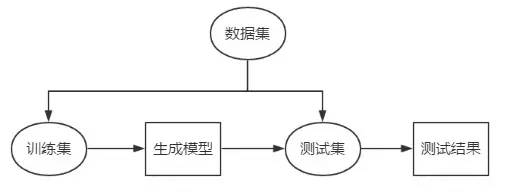
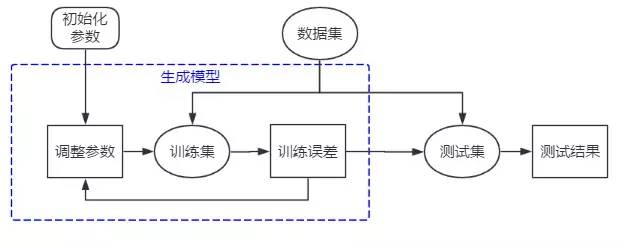
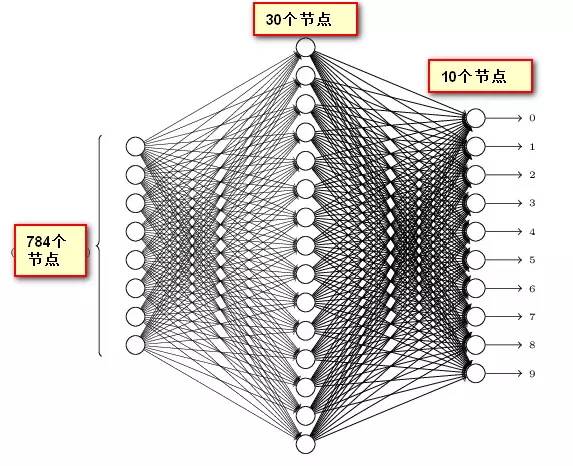
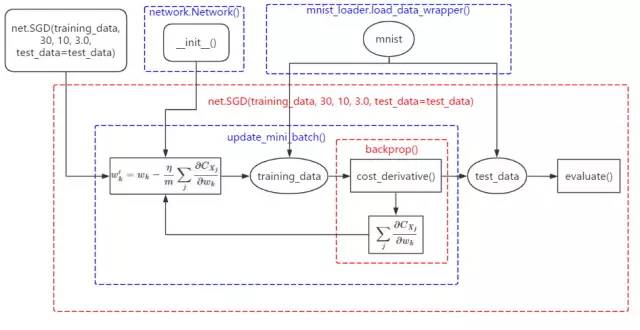
差,如果训练误差没有达到最小,我们将继续调整参数,直到这个指标达到最小。但这样训练出来的模型我们仍无法保证它面对新的数据仍会有这样好的识别效果,就需要用测试集对模型进行考核,得出的测试结果作为对模型的评价。因此,上图就可以细化成下图:


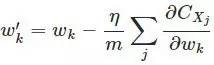
— THE END —

评论
 下载APP
下载APP日期 :2021年08月29日
正文共 :7361字
龙心尘和寒小阳:从事机器学习/数据挖掘相关应用工作,热爱机器学习/数据挖掘










— THE END —
