数据分析入门系列教程-SVM原理
SVM 的英文全称是 Support Vector Machines,我们叫它支持向量机,支持向量机是用于分类的一种算法,当然也有人用它来做回归。

SVM 原理
我们先通过一个分类的例子来看一下 SVM 的定义
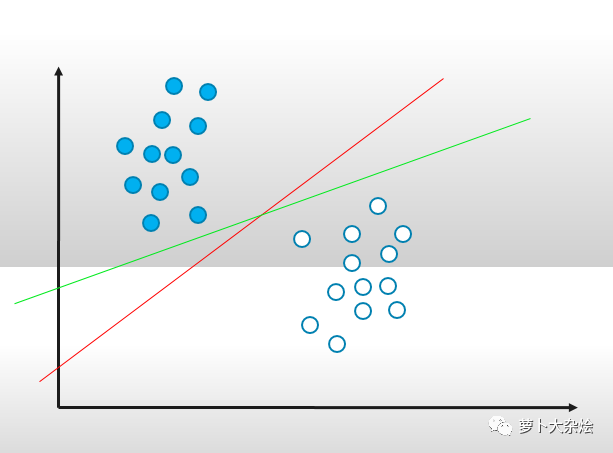
在一个二维平面上,有实心和空心两组圆点,如果我们想用一条线分开它们,那么其实可以画出无数条这种区分线。
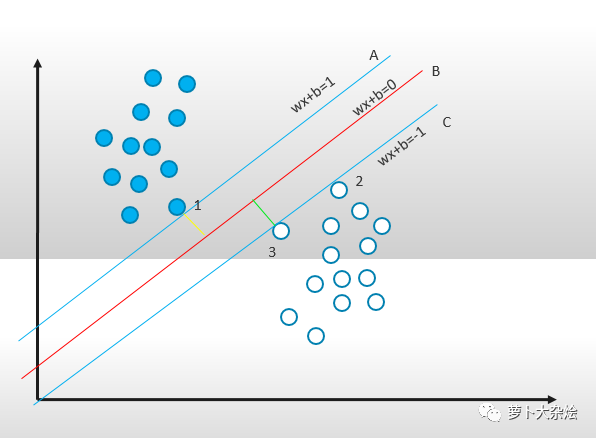
而 SVM 就是试图把线放在最佳位置,好让在线的两边到两组圆点边界点的距离尽可能大。体现在图上就是:
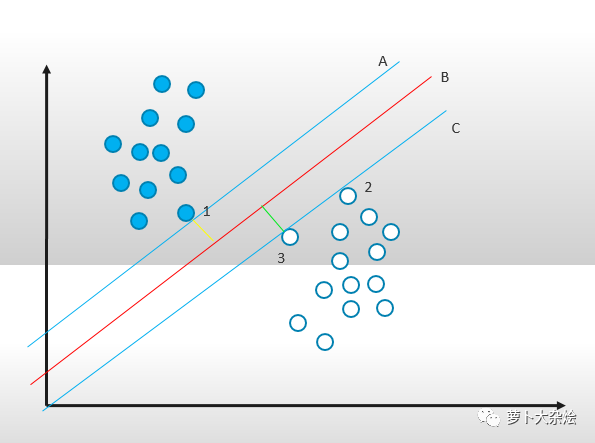
线 A 正好紧挨实心点的最边界点,线 C 正好紧挨空心点的最边界点,而线 A,B,C是三条平行线且线 B 处于线 A 和 C 距离的中心处,且图中的绿线和黄线为最大距离,则此时的线 B 即为支持向量机算法下的最优解。而点1,2,3就称为支持向量,即 support vector。
当然,还可以扩展到三维空间中,那么就是使用平面进行分割
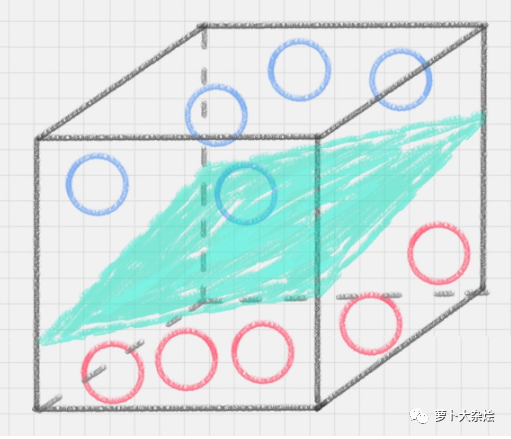
此时我们也称线 B 或者三维中的绿色平面为“决策面”。
决策面和分类间隔
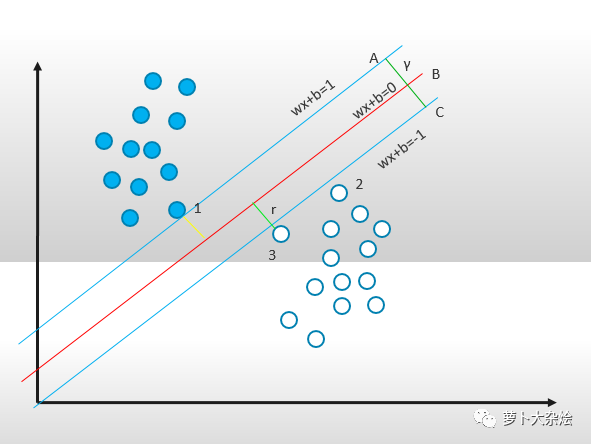
在保证决策面方向不变且不会出现错分样本的情况下移动决策面,会在原来的决策面两侧找到两个极限位置(越过该位置就会产生错分现象),如图中的两条蓝线。蓝线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定(即黄线和绿线)。而这两条平行蓝线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条蓝线之间的垂直距离就是这个最优决策面对应的分类间隔。这个具有“最大间隔”的决策面就是 SVM 要寻找的最优解。而这个真正的最优解对应的两侧蓝线所穿过的样本点,就是 SVM 中的支持样本点,称为“支持向量”,这个概念我们上面也提到了。
由上面的图示可以看出,要想找到最优的决策面,其实就是一个求解最优的问题,即最优化问题。
当然以上我们讨论的都属于线性的 SVM,对于非线性问题,在后面再做讨论
线性 SVM 数学建模
下面我们就来看看如何使用数学公式来表示 SVM
在一个最优化问题中,一般有两个最基本的因素需要解决:
目标函数,就是我们希望什么东西的什么达到最好。
优化对象,就是我们希望通过改变哪些因素来使目标函数达到最优
在 SVM 算法中,目标函数对应的应该是“分类间隔”,因为我们希望根据 SVM 的定义,我们需要找到这个最大的距离,才是 SVM 的最优解。而优化对象就是决策面,我们需要移动决策面的位置和方向,来使得分类间隔达到最大。
决策面方程
这里我们考虑的是一个两类的分类问题,数据点用 x 来表示,这是一个 n 维向量,而类别用 y 来表示,可以取 1 或者 -1 ,分别代表两个不同的类(这里类别用1和-1就是为了 SVM 公式的推导)。一个线性分类器就是要在 n 维的数据空间中找到一个超平面,其方程可以表示为
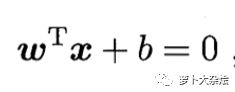
一个超平面,在二维空间中的例子就是一条直线。我们希望的是,通过这个超平面可以把两类数据分隔开来,比如,在超平面一边的数据点所对应的 y 全是 -1 ,而在另一边全是 1 。
这里的 w 和 x 都是向量,因为向量默认都是列向量,所以把 w 转置一下就变成行向量了,然后它们的乘积就是一个标量,这样就可以达到加一个标量 y 使得结果为0。
分类间隔
分类间隔说白了,就是点到直线的距离,公式为:
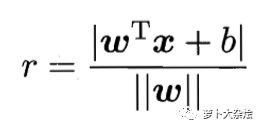
||w|| 就是向量 w 的模,即向量的长度;x 就是支持向量样本点的坐标;y 等同于决策面方程中的 y。
SVM 约束条件
我们假设超平面(w, b)可以将训练样本完全正确的分类,所以如果类别 y = 1,则有 wx + b > 0,如果 y = -1,则有 wx + b < 0。此时再根据 SVM 的定义,要想正确分类,我们需要有如下约束:
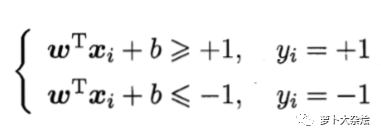
记为约束条件1
由因为两条边界线(蓝线)之间的距离 y 等于 2r,而此时 wx + b 是等于1的,所以可以得到 γ 的距离为
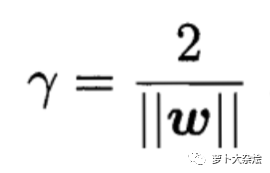
此时求解最优 SVM 就变成了求解在约束条件1下的 γ 的最大值,
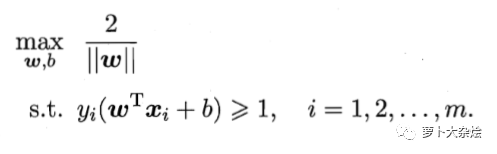
注意因为类别 y 和 wx + b 是同号的,所以它们的乘积永远为正数
也即是求 ||w|| 的最小化,即:
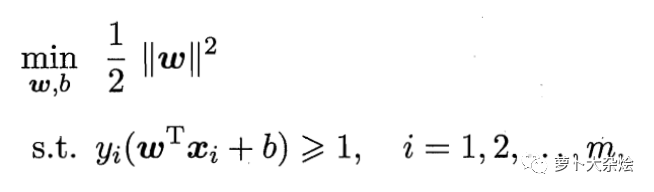
这个就是支持向量机的基本数学描述。
最后就是对上面的公式进行求解了,这中间会用到拉格朗日乘子和 KKT 等条件,就不再继续扩展了,有兴趣的同学可以查看周志华老师的《机器学习》支持向量机一篇,里面有非常详细的推导过程。
SVM 扩展
我们现在假设样本数据是完全线性可分的,那么学习到的模型就可以称之为硬间隔支持向量机,即硬间隔就是指完全正确的分类,不存在错误的情况。
但是在真实的世界中,数据往往都不是那么“干净”的,存在异常数据是再正常不过了,此时就需要软间隔。软间隔就是指允许一部分数据样本分类错误,从而使得训练的模型可以满足绝大部分其他样本。
还存在另外一种情况,就是非线性的数据集。我们前面讨论的都是线性情况下的分类,那么对于非线性的情况,SVM 也是支持的,就是非线性支持向量机。
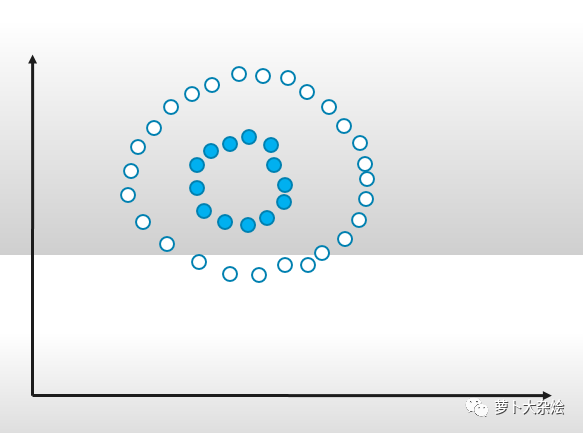
比如该类数据集,任何线性模型都没有办法处理,SVM 也是不可用的。此时,我们就需要引入一个新的概念:核函数。它可以将样本从原始的空间映射到一个更高纬度的空间中,从而使得在新的空间中样本是线性可分的,这样就可以继续使用 SVM 来做分类了。
在非线性 SVM 中,核函数的选择是影响 SVM 的最大因素。常用的核函数有线性核、多项式核、高斯核、拉普拉斯核,sigmoid 核等,或者是使用它们的组合核函数。通过这些核函数的转换,我们就可以把样本空间投射到新的高维度空间中。
SVM 实现多分类
SVM 本身是一个二值分类器,但是我们可以很方便的把它扩展到多分类的情况,这样就可以很好的应用到文本分类,图像识别等场景中。
扩展 SVM 支持多分类,一般有两种方法,OVR(one versus rest),一对多法;OVO(one versus one),一对一法。
OVR:对于 k 个类别发情况,训练 k 个SVM,第 j 个 SVM 用于判断任意一条数据是属于类别 j 还是非 j。
举个栗子:一组数据 A,B,C,我们先把其中的一类分为1,其他两类分为2,则可以构造 SVM 如下:
样本 A 为正集,B,C 为负集;
样本 B 为正集,A,C 为负集;
样本 C 为正集,A,B 为负集。
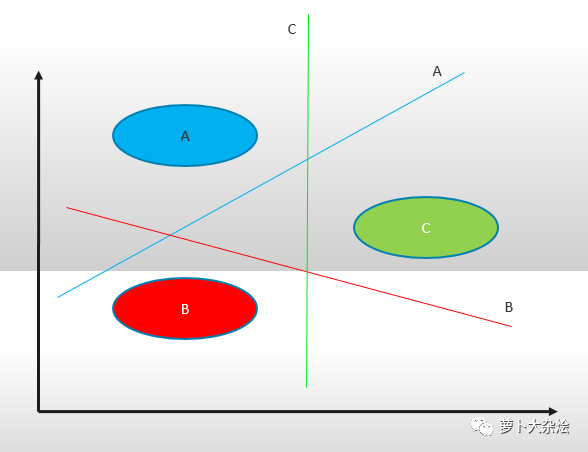
这种方法需要针对 k 个分类训练 k 个分类器,分类的速度比较快,但是训练的速度较慢。当新增一个分类时,需要重新对分类进行构造。
OVO:对于 k 个类别的情况,训练 k * (k-1)/2 个 SVM,每一个 SVM 用来判断任意一条数据是属于 k 中的特定两个类别中的哪一个。
相同的栗子:一组数据 A,B,C,我们把任意两类样本之间构造一个 SVM,那么可以构造如下:
分类器1,A,B;
分类器2,B,C;
分类器3,A,C。
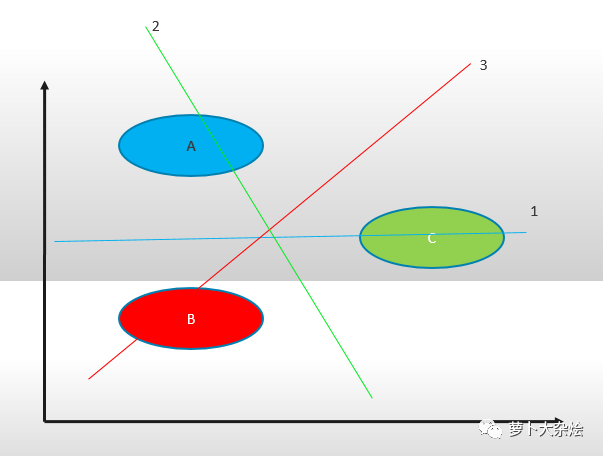
对于一个未知的样本,每一个分类器都会有一个分类结果,记票为1,最终得票最多的类别就是未知样本的类别。这样当新增类别时,不需要重新构造 SVM 模型,训练速度快。但是当 k 较大时,训练和测试时间都会比较慢。
SVM 优缺点
优点
SVM 既可以用于分类,也可以用于回归,学习能力强,学习到的结果具有很好的推广性。
SVM 是深度学习网络出现之前,机器学习领域的绝对王者
SVM 可以很好的解决小样本,高纬度问题
缺点
对于参数调节和核函数的选择很敏感
当数据量特别大时,训练很慢
总结
今天我们一起学习了 SVM 算法,可以说它是机器学习领域必备的算法,没有之一。
它本身是处理二值分类问题的,但是同样可以通过构造多个 SVM 分类器来灵活的处理多分类问题。
我们还简单的推导了在线性可分的情况下 SVM 的数学公式,而对于非线性可分的数据,我们需要引入核函数,来映射原始数据到一个新的高纬度空间中,再进行 SVM 构建。
练习题
简单的说一下,你是怎么理解硬隔离、软隔离和核函数的呢?
