AI 面试高频问题: 为什么二分类不用 MSE 损失函数?
由于微信改了推送规则,请加星标,多点赞和在看,以便第一时间收到推送。
〄机器学习与数学

对于二分类问题,损失函数不采用均方误差(Mean Squared Error,MSE)至少可以从两个角度来分析。
1从数据分布角度
首先,使用 MSE 意味着假设数据采样误差是遵循正态分布的。用贝叶斯门派的观点来看,意味着作了高斯先验的假设。实际上,可以分为两类(即二分类)的数据集是遵循伯努利分布。
如果假设误差遵循正态分布,并使用最大似然估计(Maximum Likelihood Estimation,MLE),我们将得出 MSE 正是用于优化模型的损失函数。
首先,正态/高斯分布
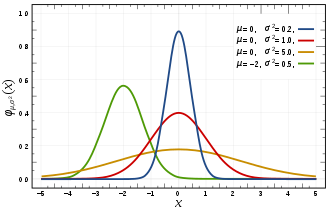
训练数据
我们可以这样来看,实际观测值
因此,每个观测值
假设数据是独立同分布的,因此使用最大似然估计时,只要最大化所有观测值误差正态分布的乘积。即似然函数为,
为了简化公式,可以采用似然函数的自然对数,
上式倒数第二行的第一项是独立于
由于方差
最后,我们可以通过
以上是通过 MLE 得到 MSE 的推导过程。这是想说明,使用 MSE 损失函数的背景假设是数据误差遵循高斯分布。实际上,二分类问题并不符合这个假设。
2从优化角度
其次,MSE 函数对于二分类问题来说是非凸的。简而言之,如果使用 MSE 损失函数训练二分类模型,则不能保证将损失函数最小化。这是因为 MSE 函数期望实数输入在范围
当将一个无界的值传递给 MSE 函数时,在目标值
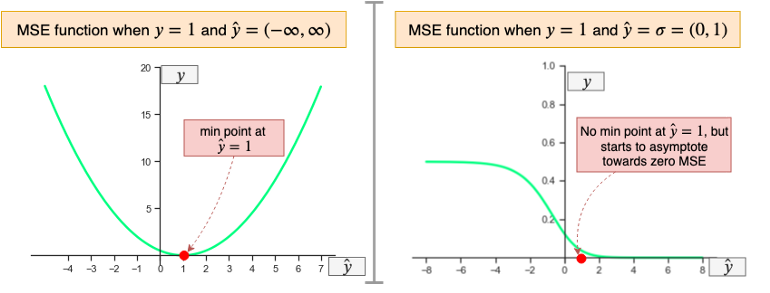
看上面右边的图,函数的一侧是凹的,而另一侧是凸的,没有明确的最小值点。因此,如果在初始化二分类神经网络权重时,权值万一设置得很大,使其落在 MSE 凹的那一侧(如下图红色标记的点),由于梯度几乎为
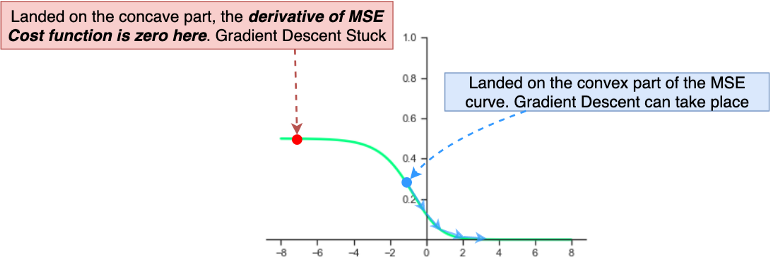
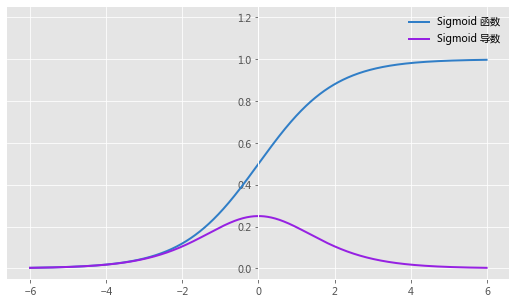
为什么是这样呢?让我们把 Sigmoid 函数代进去看看,
此时求导会多一个因子,就是
说句题外话,当我们进行线性回归(即通过直线拟合数据)时,选用 MSE 作为损失函数是一个不错的选择。在没有关于数据的分布知识的情况下,假设高斯分布通常是可行的。

3有更好选择
假如没有更好的选择,那么在权重初始化方面做做工作,MSE 也能凑合着用。但实际上,确实存在更好的选择,那就是交叉熵。戳这里可以温习一下本号关于交叉熵的图解介绍。至于为什么交叉熵在这个问题上好使,且听下回分解。
⟳参考资料⟲
正态分布: https://en.wikipedia.org/wiki/Normal_distribution
[2]Sigmoid: https://en.wikipedia.org/wiki/Sigmoid_function
[3]Rafay Khan: https://towardsdatascience.com/why-using-mean-squared-error-mse-cost-function-for-binary-classification-is-a-bad-idea-933089e90df7
