为什么说Heatmap方法是分类问题？

如果这篇文章对你有所帮助，也欢迎给我点个赞支持一下~

0. 分类问题

说到分类问题，应该是大部分同学入门深度学习时最早接触的任务了，常见的如MNIST和ImageNet数据集上进行分类，模型需要输入一张图片，然后预测该图片属于哪一个类别。

对于这类问题，目前非常成熟的做法是：让网络在倒数第二层输出一个任意长度的一维特征，然后在最后一层放一个全连接层，将倒数第二层输出的一维特征，线性变换成一个长度为N的一维向量，N对应了数据集的类别数，对这个一维向量做Softmax归一化后，用CrossEntropy即交叉熵作为损失函数进行训练。而在推理时，则是对Softmax归一化的结果取argmax，得到分数最高的那一项的位置，视为网络的预测结果，而该位置上的分数，则视为分类的置信度（当然，如果不需要置信度的话，连Softmax也不需要，因为Softmax不改变最大值的位置）。

以上过程可以用这个图来描述：

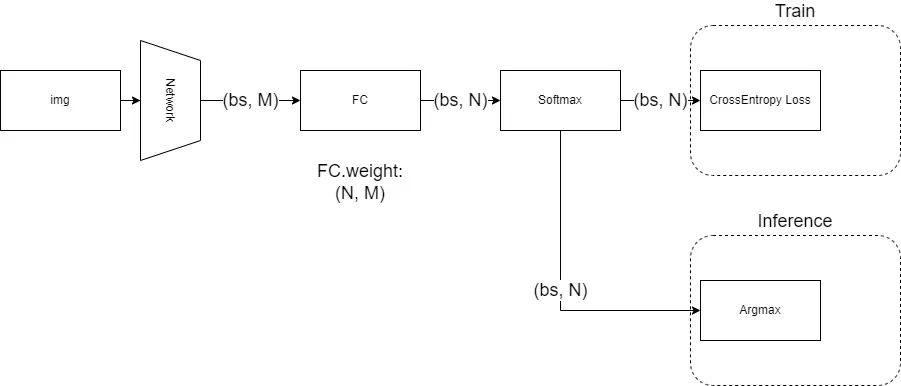
对于MNIST和ImageNet而言，我们做的都是单标签分类问题，也就是说，一张图只会对应一个类别，在网络训练时，我们训练的监督信号实际上是一个one-hot向量，即形如：[0 0 0 1 0 0]，在目标类的位置上为1，其他位置为0。

由于我们是用Softmax归一化后的结果去拟合以上one-hot向量，所以实际上这个监督信号的意思是，目标类的置信度100%，其他位置为0%，要求网络去学习这样的一个概率分布，因此原本交叉熵公式：

由于只有一个位置是1，其他位置都是0，所以硬生生变成了：

应该不难看出，这是一个非常严格的监督信号，事实上网络也的确做不到输出某一类置信度100%，但整体的学习方向和目标是没问题的，能让网络的学习目标为：目标类位置上的得分最高，其他位置上得分都比目标类低。

但事实上，大多数图片是很难做到画面中有且仅有目标类内容的，背景中难免会带点别的东西，只不过可能不是画面的主体，但对于神经网络来说，有就是有啊，这里面明明有这个东西，你却告诉我它的置信度是0%？（我做对了事还要被骂.jpg）

所以这种过于强硬的监督信号就可能带来负面作用，使网络的学习受到阻碍。

而改进方案也很有名，叫做Label Smoothing，直译的话可以叫标签软化，什么意思呢？就是说我不再那么强硬地用100%和0%，我柔和一点，目标类我用90%，其他类我都用10%，这样既不影响我原来的学习目标，又可以让画面中那些没有标注的类被预测出来时不会受到那么强的惩罚。

所以软化后的交叉熵公式回到了原本的形式：

对分类问题进行了以上简单介绍后，那么在关键点定位时Heatmap方法是怎么做的呢？

1. 定位问题

在为任何问题设计目标函数时，我们都必须明确我们的任务目标是什么，对于图片分类问题，我们的目标是：目标类位置上的得分最高，其他位置上得分都比目标类低。

类比到关键点定位问题，我们的目标应该是：目标点位置上的得分最高，其他位置上得分都比目标点低。

这样一看，是不是就会发现定位问题本质上还是一个分类问题了？

所以按照这个思路，我们也可以想到，最原始的监督信号，也应该是一个one-hot的标注，即在一张二维平面上，只有目标点所在的像素标注为1，其他位置都为0，如果把这个二维向量拉直，那形状就跟一维分类一模一样：[0 0 0 1 0 0]

那么这样做有什么不好呢？同样类比分类问题，还是标注信息惹的祸：在关键点标注时，我们没法保证真的做到刚好在关键点那个像素标注1，毕竟人都是会犯错的，再加上实际图片往往还可能有模糊不清、遮挡等因素，标注的结果跟真实位置有一点点偏移是再正常不过的了。

考虑到这个因素，再用one-hot去监督就明显不太好了，有时候网络也许明明预测到了真实位置，却因为标注员的标注点歪了一个像素，导致网络受到严厉惩罚，这对于性能自然是有很大影响的。

改进方案也很自然，Label Smoothing嘛，但这一次却不能像分类问题那样0.9和0.1地来了，我们选择了用高斯分布来渲染标签。

为什么呢？实际上，用高斯分布是引入了我们的一个先验知识，即：离目标点越近的像素得分应该越高，目标点上的得分最高。 这个先验知识是定位问题独有的，而对分类问题显然不适用，至于为什么用高斯分布，来自于中心极限定理的保证——任何大的数据都趋近于高斯分布，你怎么用它几乎都是对的。

也很自然地可以想到，高斯分布只是一个很中庸的选择，根据数据的真实分布，我们大可以选择更好的分布来进行监督，能取得更好的效果。

经过了软化的标签，即使标注信息有所偏移，但由于偏移通常也就几个像素，所以网络预测正确受到的惩罚相较于预测错误还是小很多的。

2. 一点点延伸

其实上面已经交代清楚了本文的标题：为什么说Heatmap方法是分类问题。下面我进行一点点的延伸：

(1)

用卷积神经网络做定位问题的一个优势在于，卷积网络的本身是用一个个卷积核在图片平面上滑动，就像在对目标内容做模式匹配一样，这跟用全连接层拟合概率分布相比，保留了很多空间信息，因此效率上高多了。

(2)

分类问题的本质，回到网络结构上，网络最后一层的全连接层是一个矩阵运算，假如倒数第二层输出的特征维度为M，类别数为N，那么这个矩阵的形状就是(N, M)，可以看成是N个长度为M的向量。

从数学意义上，这个全连接层在做的，是让网络预测的特征向量，分别跟全连接层里学到的N个向量求内积，所以才会越相似的向量之间内积越大。

所以这背后的本质，是网络在为每个类学习一个聚类中心。

(3)

对于标准的分类问题而言，总的类别数是固定的，不会莫名其妙多几类或者少几类，但是对定位问题来说，输出的heatmap分辨率不同，这分类问题的类别数是不是就变化了？

分辨率越小，类别数就越少，即我们需要学习的聚类中心向量也少，那么这个分类问题就越简单；分辨率越大，类别数越多，每个聚类中心向量都学好的难度也就越大。

假如我们让情况变得极端一点，网络预测的heatmap最小可以是1x1，即只有一个像素，那么这个时候，网络预测的结果就变成了一个0-1的二分类问题，也就是在预测关键点的存在性。

所以关键点的存在性问题，实际上只是关键点定位问题的一个特殊情况，并且是难度最低的情况，也因此，在很多业务中我们需要知道每个点存在的概率时，与其用最大响应值点的置信度来作为存在性判断，不如直接用一个头部来做二分类准确度高。

另一种极端情况是网络预测的heatmap变大，当heatmap跟输入图片一样尺寸时，我们的分类问题就成了对原图片每一个像素进行分类；假如我们的heatmap比原图片还大，那我们的分类问题就是在亚像素上做的：错误的量化误差变成1/s。（当然，代价是指数级上升的计算量，以及过拟合的风险）

3. 尾语

这篇文章内容实际上很基础，之所以写出来一方面是对自己知识的一种梳理，另一方面也是受益于近期仔细拜读了知乎上王峰大佬的Softmax系列文章，尽管大佬是做人脸识别任务，但cv领域原本就是一通百通的，读后我感觉收获非常大，在此也强烈推荐大家前往阅读。

https://zhuanlan.zhihu.com/p/45014864

如果这篇文章对你有所帮助，欢迎给我点个赞支持一下，我们下期再见~