十大经典排序算法之希尔排序算法
点击上方蓝字关注我们
希尔排序
之前我们讲过冒泡排序、选择排序、插入排序,它们的时间复杂度都是 ,比较高,在实际的场景用应用也比较少。
今天我们要讲的希尔排序虽然也是插入排序的一种,但是它是插入排序的一个高效变形,脱离了 的时间复杂度深渊。
主要思想
希尔排序的思想简单点说就是有跨度的插入排序,这个跨度会逐渐变小,直到变为 1,变为 1 的时候也就是我们之前讲的简单插入排序了。
规范点的描述就是,选择一组递减的整数作为增量序列,最小的增量必须为 1。
先用第一个增量把数组分为若干个子数组,每个子数组中的元素下标距离等于增量; 然后对每个子数组进行简单插入排序 再使用第二个增量,然后继续同样的操作,直到增量序列里的增量都使用过一次(增量为 1 时,其实就是对整个数组进行简单插入排序)。
可能你有点疑惑为啥刚开始要进行大跨度的插入排序呢?说实话我刚开始的时候也觉得怪怪的,举个极端的例子帮助你理解下。
假定 ,对于简单的插入排序,如果最小的元素位于最后面的话,那么它就需要和所有的元素比较移动一遍,才可以到达它指定的位置,但是刚开始进行大跨度插入排序的时候,它就可以少比较几次就可以到达前面了。
这就是希尔排序的思想。
代码实现
#!/usr/bin/python
# -*- coding: utf-8 -*-
from typing import List
import random
def shell_sort_original(array: List[int]) -> None:
# 增量序列的初始值
gap = len(array) // 2
while gap > 0:
# 对于 array 进行分组,默认编号是 0, 1, 2, ...
for i in range(gap):
# 对于每组进行插入排序
for j in range(i+gap, len(array), gap):
temp = array[j]
index = j - gap
while index >= 0:
if array[index] > temp:
array[index+gap] = array[index]
index -= gap
else:
break
array[index+gap] = temp
# 增量序列值减小,变为原来的 1/2
gap //= 2
if __name__ == "__main__":
min_number, max_number = 0, 100
num = 10
array = [random.randint(min_number, max_number) for _ in range(num)]
print(array)
shell_sort_original(array)
print(array)
乍一看,这个程序一共有四层循环,是不是觉得这个程序怎么可能是插入排序的优化算法呢?但是这个确实是按照希尔排序的思想进行写出来的。
确实,这个程序确实是四层循环,但是呢一个程序的时间复杂度不能单单看循环的层数,更应该看的是程序随着输入的执行次数。
希尔排序的写法优化
虽然上面的写法就是完全按照希尔排序的思想来进行实现的,但是呢,写的不够简洁。
下面带你看下一个更常用的写法:
#!/usr/bin/python
# -*- coding: utf-8 -*-
from typing import List
import random
def shell_sort(array: List[int]) -> None:
# 增量序列
gap = len(array) // 2
while gap > 0:
for i in range(gap, len(array)):
temp = array[i]
index = i - gap
while index >= 0:
if array[index] > temp:
array[index + gap] = array[index]
index -= gap
else:
break
array[index+gap] = temp
gap //= 2
if __name__ == "__main__":
min_number, max_number = 0, 100
num = 10
array = [random.randint(min_number, max_number) for _ in range(num)]
print(array)
shell_sort(array)
print(array)
这种实现方法在表面上模糊了对数组分组的概念,而是在进行插入排序的时候通过设置 的变化值为 (之前是 1),来实现的。
性能分析
希尔排序的时间复杂度不是我们表面认为的那样,一般来说认为希尔排序的时间复杂度是 ,这个证明起来比较难。
空间复杂度的话,希尔排序没有使用额外的空间,进行存储,是原地排序算法。
希尔排序算法不是稳定的排序算法。前面我们也提到过,只要涉及到大跨度的排序算法,一般都不是稳定的排序算法。
优化
希尔排序的优化主要是针对增量序列的优化。增量序列如果取得不好,效率比直接插入排序还要低,下面举个例子1:
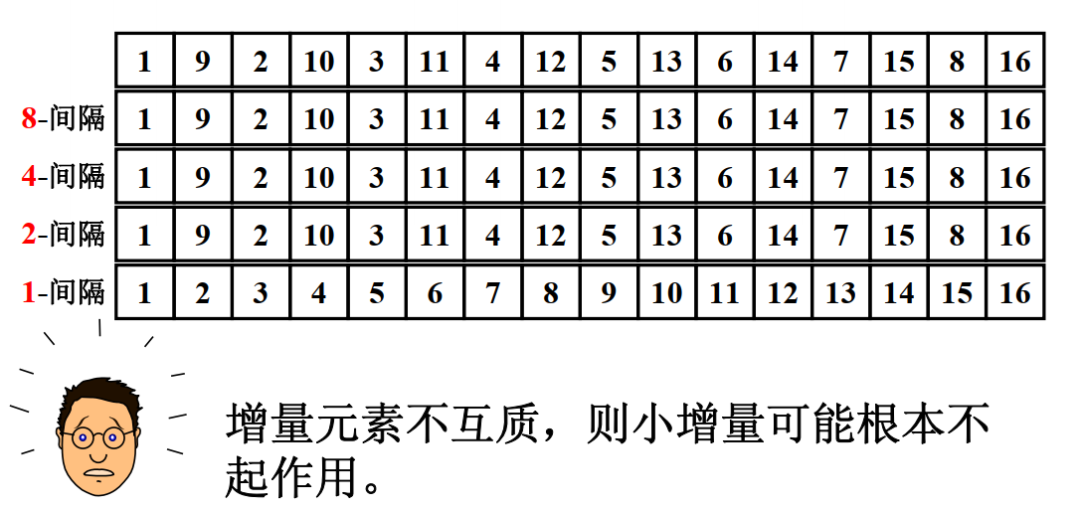
这个例子就形象说明了这个问题。
于是呢,人们就研究了一些比较好用的增量序列,比如说Hibbard增量序列、Sedgewick增量序列。
Hibbard增量序列
Hibbard增量序列的取法为
Sedgewick增量序列
Sedgewick增量序列的取法为
总结
本文主要介绍了希尔排序的思想及其代码实现,通过其两种代码实现也可以看到计算机的理论和实现还是不一样的,在理解理论的同时还需要多实践才能更好的学习编程。
一个人可以走的更快,一群人可以走得更远
长按扫码关注我们

