复现了LeCun 33年前的神经网络-技术圈

↓↓↓点击关注，回复资料，10个G的惊喜

选自Andrej Karpathy blog 作者：Andrej Karpathy 机器之心编译

最近，特斯拉 AI 高级总监 Andrej Karpathy 做了一件很有趣的事情，他把 Yann LeCun 等人 1989 年的一篇论文复现了一遍。一是为了好玩，二是为了看看这 33 年间，深度学习领域到底发生了哪些有趣的变化，当年的 LeCun 到底被什么卡了脖子。此外，他还展望了一下 2055 年的人将如何看待今天的深度学习研究。

1989 年，Yann Lecun 等人发表了一篇名为「Backpropagation Applied to Handwritten Zip Code Recognition」的论文。在我看来，这篇论文有一定的历史意义，因为据我所知，它是使用反向传播训练的端到端神经网络在现实世界中最早的应用。

论文链接：http://yann.lecun.com/exdb/publis/pdf/lecun-89e.pdf

尽管数据集和神经网络都比较小（7291 张 16x16 灰度数字图像，1000 个神经元），但这篇论文在 33 年后的今天读起来依然没感觉过时：它展示了一个数据集，描述了神经网络的架构、损失函数、优化，还给出了训练集和测试集的实验分类错误率。它是那么得有辨识度，完全可以被归类为现代深度学习论文，但它却来自 33 年前。所以我开始复现这篇论文，一是为了好玩，二是为了将此练习作为一个案例研究，探讨深度学习进步的本质。

实现

我试着尽可能地接近论文，并在 PyTorch 中复现了每个细节，参见以下 GitHub 库：

复现链接：https://github.com/karpathy/lecun1989-repro

最初的网络是用 Lisp 实现的，使用了 Bottou 和 LeCun 1988 年提出的反向传播模拟器 SN（后来被命名为 Lush）。这篇论文是法语的，所以我读不懂。但从句法来看，你可以使用高级 API 指定神经网络，类似于今天在 PyTorch 中做的事情。

在当代软件设计中，库的设计分为以下 3 个部分：

1）一个快速 (C/CUDA) 通用 Tensor 库，用来实现多维张量的基本数学运算；

2）一个 autograd 引擎，用来跟踪前向计算图并为 backward pass 生成运算；

3）一个可脚本化的（Python）深度学习、高级 API，包含常见的深度学习运算、层、架构、优化器、损失函数等。

训练

在训练过程中，我们要对 7291 个样本组成的训练集进行 23 次 pass，总共有 167693 个样本 / 标签展示给神经网络。最初的网络在一个 SUN-4/260 工作站（发布于 1987 年）上训练了 3 天。现如今，我用我的 MacBook Air (M1) CPU 就能运行这个实现，而且只用了 90 秒（实现了大约 3000 倍的加速）。我的 conda 被设置为使用本机 amd64 构建，而不是 Rosetta 模拟。如果 PyTorch 能够支持 M1 的所有功能（包括 GPU 和 NPU），那么加速效果可能会更加明显。

我还尝试单纯地在一个 A100 GPU 上运行代码，但训练却更慢，原因很可能是网络太小（4 层 convnet，最多 12 个通道，总共 9760 个参数，64K MACs，1K 激活），并且 SGD 一次只使用一个示例。也就是说，如果一个人真的想用现代硬件（A100）和软件基础设施（CUDA，PyTorch）来解决这个问题，我们需要把 per-example SGD 换成 full-batch 训练，以最大限度地提高 GPU 利用率。这样一来，我们很有可能额外实现约 100 倍的训练加速。

复现 1989 年的实验结果

原始论文给出了以下实验结果：

eval: split train. loss 2.5e-3. error 0.14%. misses: 10eval: split test . loss 1.8e-2. error 5.00%. misses: 102

但在第 23 轮 pass 之后，我的训练脚本 repro.py 打印出的结果却是：

eval: split train. loss 4.073383e-03. error 0.62%. misses: 45eval: split test . loss 2.838382e-02. error 4.09%. misses: 82

所以，我只是粗略复现了论文的结果，数字并不精确。想要得到和原论文一模一样的结果似乎是不可能的，因为原始数据集已经随着时间的流逝而丢失了。所以，我必须使用更大的 MNIST 数据集来模拟它，取它的 28x28 digits，用双线性插值将它们缩小到 16x16 像素，并随机而不替换地从中抽取正确数量的训练和测试集示例。

但我确信还有其他影响精确复现的原因，如这篇论文对权重初始化方案的描述有点过于抽象；PDF 文件中可能存在一些格式错误（小数点、平方根符号被抹掉等等）。例如，论文告诉我们，权重初始化是从统一「2 4 / F」中提取的，其中 F 是 fan-in，但我猜这里实际是「2.4 / sqrt(F)」，其中的 sqrt 有助于保持输出的标准差。H1 和 H2 层之间特定的稀疏连接结构也有问题，论文只说它是「根据一个方案选择的，这个方案先按下不表」，所以我不得不用重叠的块稀疏结构做一些合理的猜测。

该论文还声称使用了 tanh non-linearity，但是我担心这可能实际上是映射 ntanh(1) = 1 的「normalized tanh」，并有可能添加了一个缩小的残差连接，这在当时非常流行，以确保 tanh 的平尾至少有一点梯度。最后，该论文使用了「牛顿法的特殊版本，该版本使用了 Hessian 的正对角近似」。但我只用了 SGD，因为它明显更简单。而且，论文作者表示，「这种算法被认为不会带来学习速度的巨大提升」。

用新方法试试

这是我最喜欢的部分。我们生活在 33 年后的今天，深度学习已经是一个非常活跃的研究领域。利用我们现在对深度学习的理解以及这 33 年积累的研发经验，我们能在原结果的基础上做出多少改进呢？

我最初的结果是：

eval: split train. loss 4.073383e-03. error 0.62%. misses: 45eval: split test . loss 2.838382e-02. error 4.09%. misses: 82

首先需要明确，我们正在进行 10 个类别的简单分类。但当时，这被建模为 targets -1（针对负类）或 + 1（针对正类）的均方误差（MSE）回归，输出神经元也具有 tanh non-linearity。因此，我删除了输出层上的 tanh 以获得 class logits，并在标准（多类）交叉熵损失函数中进行交换。这一变化极大地提高了训练错误，使训练集完全过拟合：

eval: split train. loss 9.536698e-06. error 0.00%. misses: 0eval: split test . loss 9.536698e-06. error 4.38%. misses: 87

我怀疑，如果你的输出层有（饱和的）tanh non-linearity 和 MSE 误差，你必须更加小心权重初始化的细节。其次，根据我的经验，一个微调过的 SGD 可以运行得很好，但是当前 Adam 优化器（3e-4 的学习率）几乎总是一个很好的基线，几乎不需要调整。

因此，为了让我更加确信优化不会影响性能，我切换到了 AdamW with，同时将学习率设置为 3e-4，并在训练过程中将学习率降至 1e-4。结果如下：

eval: split train. loss 0.000000e+00. error 0.00%. misses: 0eval: split test . loss 0.000000e+00. error 3.59%. misses: 72

这在 SGD 的基础上给出了一个稍微改进的结果。不过，我们还需要记住，通过默认参数也有一点权重衰减，这有助于对抗过拟合的情况。由于过拟合仍然严重，接下来我引入了一个简单的数据增强策略：将输入图像水平或垂直移动 1 个像素。但是，因为这模拟了数据集的增大，所以我还必须将通道数从 23 增加到 60（我验证了在原始设置中简单地增加通道数并不能显著改善结果）：

eval: split train. loss 8.780676e-04. error 1.70%. misses: 123eval: split test . loss 8.780676e-04. error 2.19%. misses: 43

从测试错误中可以看出，上述方法很有帮助！在对抗过拟合方面，数据增强是一个相当简单、标准的概念，但我没有在 1989 年的论文中看到它，也许这是一个出现略晚的创新？由于过拟合仍然存在，我从工具箱里拿出了另一个新工具——Dropout。我在参数数量最多的层（H3）前添加了一个 0.25 的弱 dropout。因为 dropout 将激活设置为零，所以它与活动范围为 [-1，1] 的 tanh 一起使用没有多大意义，所以我也将所有 non-linearities 替换为更简单的 ReLU 激活函数。因为 dropout 会在训练中引入更多的噪声，我们还必须训练更长的时间，pass 数达到 80。最后得到的结果如下：

eval: split train. loss 2.601336e-03. error 1.47%. misses: 106eval: split test . loss 2.601336e-03. error 1.59%. misses: 32

这使得我们在测试集上只有 32/2007 的错误！我验证过，仅仅在原始网络中将 tanh 换成 relu 并没有带来实质性的收益，所以这里的大部分改进来自于 dropout。总的来说，如果我回到 1989 年，我将把错误率降低 60%（把错误数从 80 降到 30 个），测试集的总错误率仅为 1.5%。但这一收益并不是「免费的午餐」，因为我们几乎增加了 3 倍的训练时间（从 3 天增加到 12 天）。但是推理时间不会受到影响。剩下的错误如下：

再进一步

然而，在完成 MSE → Softmax、SGD → AdamW 的转变，增加数据增强、dropout，以及将 tanh 换成 relu 之后，我开始逐渐放弃那些容易实现的想法，转而尝试更多的东西（如权重归一化)，但没有得到实质上更好的结果。

我还试图将一个 ViT 缩小为一个与参数和 flops 数量大致匹配的「微型 ViT」，但它无法与一个卷积网络的性能相媲美。当然，在过去的 33 年里，我们还看到了许多其他的创新，但是其中的许多（例如残差连接、层 / 批归一化）只能在大模型中发挥作用，而且主要用于稳定大模型的优化。在这一点上，进一步的收益可能来自于网络规模的扩大，但是这会增加测试时推理的延迟。

在数据上动手脚

提高性能的另一种方法是扩大数据集的规模，尽管这需要花费一美元的标签成本。这里再贴一下我们的原始基线：

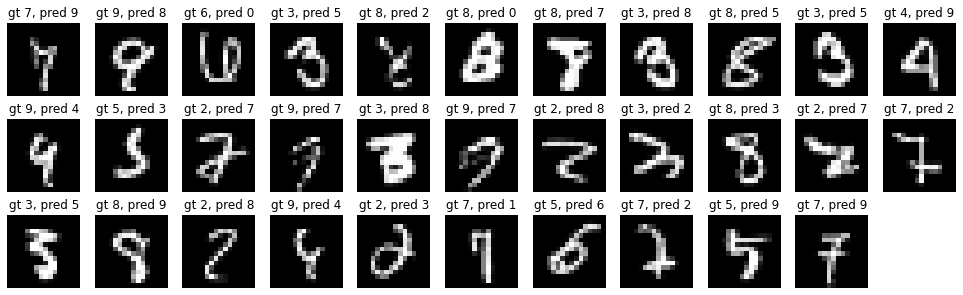
eval: split train. loss 4.073383e-03. error 0.62%. misses: 45eval: split test . loss 2.838382e-02. error 4.09%. misses: 82

由于现在可以使用整个 MNIST，我们可以将训练集规模扩大到原来的 7 倍（从 7291 扩大到 50000）。仅从增加的数据来看，让基线训练跑 100 pass 已经显示出了一些改进：

eval: split train. loss 1.305315e-02. error 2.03%. misses: 60eval: split test . loss 1.943992e-02. error 2.74%. misses: 54

进一步将其与现代知识的创新相结合（如前一节所述），将获得最佳性能：

eval: split train. loss 3.238392e-04. error 1.07%. misses: 31eval: split test . loss 3.238392e-04. error 1.25%. misses: 24

总之，在 1989 年，简单地扩展数据集将是提高系统性能的一种有效方法，而且不会影响推理延迟。

反思

让我们总结一下，作为一个来自 2022 年的时间旅行者，我们从 1989 年的深度学习 SOTA 技术中学到了什么：

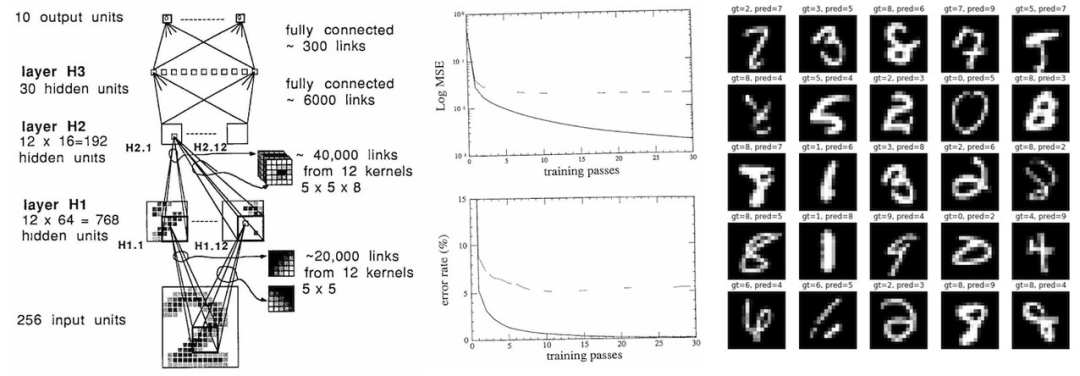
首先，33 年来的宏观层面没有太大变化。我们仍然在建立由神经元层构成的可微神经网络体系架构，并使用反向传播和随机梯度下降对它们进行端到端优化。一切读起来都非常熟悉，只是 1989 年的网络更小。
以今天的标准来看，1989 年的数据集还是个「婴儿」: 训练集只有 7291 张 16x16 的灰度图像。今天的视觉数据集通常包含来自网络的几亿张高分辨率彩色图像（谷歌有 JFT-300M，OpenAI CLIP 是在 400M 张图上训练的），而且会增长到几十亿张的规模。每张图像包含的像素信息增长了 1000 倍（384 * 384 * 3/(16 * 16)），图像数量增长了 100,000 倍（1e9/1e4），粗略计算的话，像素数据输入增长了 100,000,000 倍以上。
那时的神经网络也是一个「婴儿」：它大约有 9760 个参数、64K MACs 和 1K activations。当前（视觉）神经网络的规模达到了几十亿参数，而自然语言模型可以达到数万亿参数。

当年，一个 SOTA 分类器在工作站上训练需要 3 天，现在如果是在无风扇笔记本电脑上训练只需要 90 秒（3000 倍加速），如果切换到 full-batch 优化并使用 GPU，速度还能提升百倍以上。
事实上，我能够通过微调模型、增强、损失函数，以及基于现代创新的优化，将错误率降低 60% ，同时保持数据集和模型测试时间不变。
仅仅通过扩大数据集就可以获得适度的收益。
进一步的重大收益可能必须来自一个更大的模型，这将需要更多的计算和额外的研究与开发，以帮助稳定规模不断扩大的训练。如果我被传送到 1989 年，而且没有一台更大的计算机，我将无法进一步改进系统。

假设这个练习课程时间上保持不变，这对 2022 年的深度学习意味着什么？一个来自 2055 年的时间旅行者会如何看待当前网络的表现？

2055 年的神经网络在宏观层面上基本上与 2022 年的神经网络相同，只是规模更大。
我们今天的数据集和模型看起来像个笑话，2055 年的二者规模都大约有 10,000,000 倍。
一个人可以在一分钟内训练 2022 个 SOTA 模型，而且是在他们的个人电脑上作为一个周末娱乐项目来训练。
今天的模型并不是最优化的，只是改变了模型的一些细节、损失函数、增强或者可以将误差降低一半的优化器。
我们的数据集太小了，通过扩大数据集可以获得适度的收益。
如果不扩大计算机基础设施和投资相应规模的高效训练模式的研发，就不可能取得进一步的收益。

但我想要表达的最重要的趋势是，随着 GPT 这种基础模型的出现，根据某些目标任务（比如数字识别）从零开始训练整个神经网络的设置，会由于「微调」而变得落伍。这些基础模型由那些拥有大量计算资源的少数机构进行训练，大多数应用是通过对网络的一部分进行轻量级微调、prompt engineering，或是通过数据和模型蒸馏到更小的专用推理网络的 optional step 来实现的。

我认为，这一趋势在未来将十分活跃。大胆假设一下，你根本不会再想训练一个神经网络。在 2055 年，你可以用说话的方式去要求一个 10,000,000 倍大小的神经网络大脑去执行一些任务。如果你的要求足够明确，它就会答应你。

当然，你也可以自己训练一个神经网络，但你为什么要这么做呢？

原文链接：https://karpathy.github.io/2022/03/14/lecun1989/

AI黑科技！从此只看高清视频
AI 黑科技，老照片修复，模糊变高清
朴实无华，万字统计学知识大梳理
机器学习理论基础到底有多可靠？
人工智能博士：思维修炼指南
“卷积”其实没那么难以理解