“约瑟夫问题”教学思路
说在前面
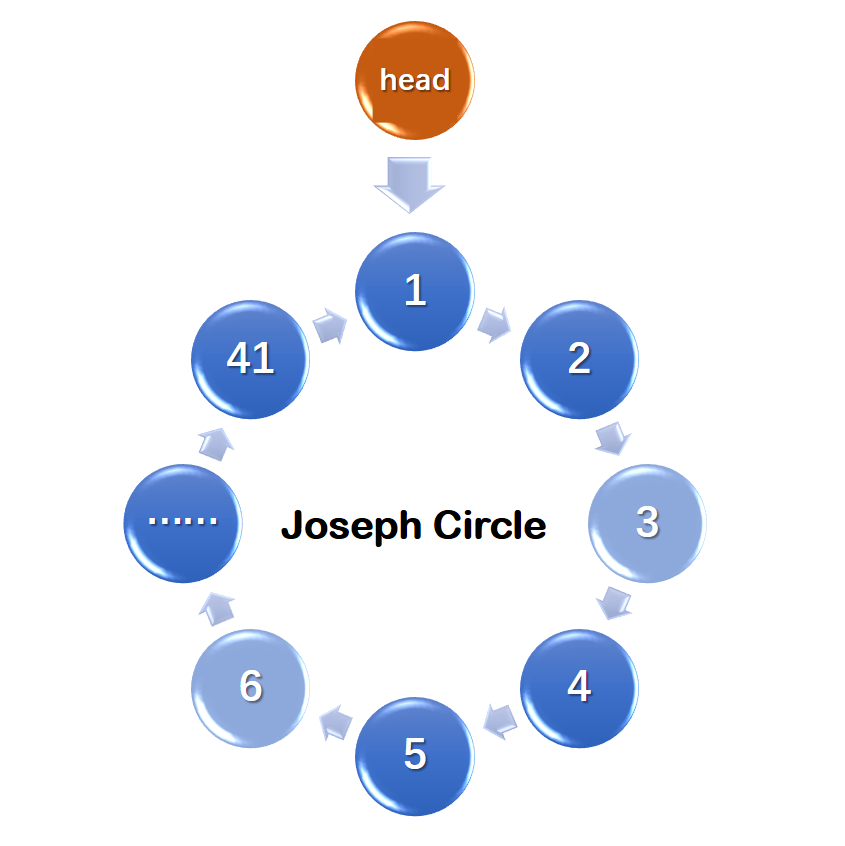
约瑟夫问题是一个经典的数学应用问题，它通过循环报数不断删除序列中的元素，直至剩下1个（或多个）人为止。编程解决约瑟夫问题的算法很多，基本思想都是模拟报数过程，区别在于数据结构不同，删除元素的方法也不一样。
约瑟夫问题可以考查使用模运算实现循环报数功能，使用循环链表、循环队列等数据结构模拟报数和删除元素过程，变例繁多、算法难度较高、综合性强，是需要重点掌握的经典案例。
教材文本
n=int(input("请输入参与人数（N）："))
m=int(input("请输入淘汰数（M）："))
a = [[i+1,i+1] for i in range(n-1)]
a.append(填空1) # 最后一个人的下一位是第一个人
pre = len(a) - 1 # 指向前驱节点
while 填空2: # 循环单链表中节点数量大于1
for i in range(1, m): # 报数[1,m-1]的人留下
pre = 填空3
a[pre][1] = 填空4 # 报数m的人离开（删除a[pre][1]）
print(f'幸存者位置为：{a[pre][0]}')
if i==m: # 报数为m时删除k的后继节点t
t=a[k][1] # 用t指向节点k的后继节点
a[k][1]=a[t][1] # 修改k的后继指针，以实现删除节点t功能
if t==head: # 删除头节点时需要修改头指针
head=a[k][1] # 或者head=a[t][1]
i=1 # 计数器归1
long-=1 # 链表长度减1
程序通过修改k的后继指针，实现删除其后继节点的功能。为了增强代码的可读性，程序设置变量t指向节点k的后继节点，然后修改a[k][1]=a[t][1]，这样就能实现删除节点t的功能了。为了使head始终指向链表的头节点，当被删除节点是头节点时需要修改头指针head。
删除某个节点后，程序让计数器i归1，并使记录链表长度的变量long减1，准备下一轮报数。
n=int(input("请输入参与人数（N）："))
m=int(input("请输入淘汰数（M）："))
a = [[i+1,i+1] for i in range(n-1)]
a.append([n, 0]) # 最后一个人的下一位是第一个人
pre = len(a) - 1 # 指向前驱节点
while a[pre][1] != pre: # 循环单链表中节点数量大于1
for i in range(1, m): # 报数[1,m-1]的人留下
pre = a[pre][1]
a[pre][1] = a[a[pre][1]][1] # 报数m的人离开（删除a[pre][1]）
print(f'幸存者位置为：{a[pre][0]}')
教材程序通过遍历链表来模拟报数过程，并删除节点以实现淘汰人员功能，直至只剩一个节点为止。除此之外，你还能想到别的方法来解决约瑟夫问题吗？例如使用一维数组和循环队列等数据结构来存储数据，又该如何编写代码呢？
需要本文word文档、源代码和课后思考答案的，可以加入“Python算法之旅”知识星球参与讨论和下载文件，“Python算法之旅”知识星球汇集了数量众多的同好，更多有趣的话题在这里讨论，更多有用的资料在这里分享。
我们专注Python算法，感兴趣就一起来！
相关优秀文章：