关于卡尔曼及卡尔曼增益的理解【精】
点击下方卡片,关注“新机器视觉”公众号
视觉/图像重磅干货,第一时间送达
提到卡尔曼,不得不说一个故事:
片绿油油的草地上有一条曲折的小径,通向一棵大树。一个要求被提出:从起点沿着小径走到树下。
“很简单。” A说,于是他丝毫不差地沿着小径走到了树下。
现在,难度被增加了:蒙上眼。
“也不难,我当过特种兵。” B说,于是他歪歪扭扭地走到了树旁。“唉,好久不练,生疏了。” (只凭自己的预测能力)
“看我的,我有 DIY 的 GPS!” C说,于是他像个醉汉似地歪歪扭扭的走到了树旁。“唉,这个 GPS 没做好,漂移太大。”(只依靠外界有很大噪声的测量)
“我来试试。” 旁边一也当过特种兵的拿过 GPS, 蒙上眼,居然沿着小径很顺滑的走到了树下。(自己能预测+测量结果的反馈)
“这么厉害!你是什么人?”
“卡尔曼 ! ”
“卡尔曼?!你就是卡尔曼?”
众人大吃一惊。
“我是说这个 GPS 卡而慢。
总结就是预测+测量更新。
卡尔曼滤波的测量更新部分是由最小二乘推导而来。

今天主要说明卡尔曼增益的Kt如何去理解?
卡尔曼主要来处理如下两个来源的数据:
(1)根据模型来预测出的数据。(预测)
(2)传感器观测到的数据。(观测)
核心:
K越小越相信你的预测(1)中的估计,
K越大越相信你的观测(2)中的观测。
K的值和传感器的精度有关。依赖于按个传感器更缺。
我们从另一个角度理解卡尔曼滤波算法,假设你的传感器和预测模型的噪声均满足正高斯正态分布,看下面图片:
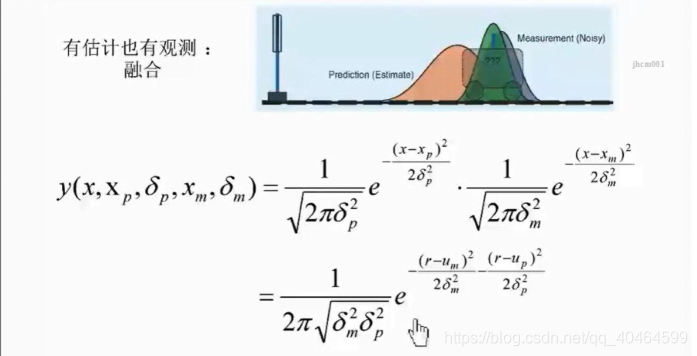
显然你可以看到两个正态分布相乘,带P下坠的代表预测满足的噪声正态分布,带m下标的表示是传感器测量噪声所满足的正态分布。这两个预测和测量是独立事件。

整理后得到上述的式子。我们会得到如下分析:
(1)δp越大时,k越大,这样对于预测来说它的噪音的不确定性变大,所以我们相信更传感器的测量值
(2) δp越小的时候,k越小,这样对于预测来说它的噪音不确定性变小,所以我们更相信预测的值。

现在,我们把一维推广到高维,用矩阵表示:
比如高维情况下卡尔曼增益K=P*Ht*(R+HPHt)(图中绿框地方),这个式子与正好对应。

P是预测的方差,H是观测矩阵,R是传感器测量满组方差。其余也是一一对应的。
版权声明:本文为CSDN博主「Jack Ju」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:
https://blog.csdn.net/qq_40464599/article/details/108106552
编辑:古月居
声明:部分内容来源于网络,仅供读者学习、交流之目的。文章版权归原作者所有。如有不妥,请联系删除。
—THE END—
