PyTorch学习系列教程：三大神经网络在股票数据集上的实战-技术圈

导读

近几天的推文中，分别对深度学习中的三大神经网络——DNN、CNN、RNN进行了系统的介绍，今天本文以股票数据集为例对其进行案例实战和对比。

对这三类神经网络不熟悉的读者，欢迎查看历史推文：

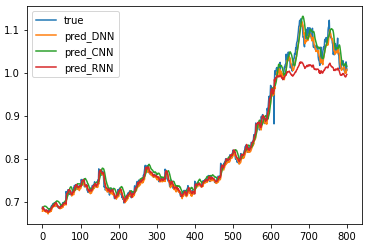
DNN、CNN和RNN是深度学习中的三大经典神经网络，分别有各自的适用场景。但为了能够在同一任务下综合对比这三种网络，本文选择对股票预测这一任务开展实验，其中DNN可以将历史序列特征转化为全连接网络，而CNN则可利用一维卷积进行特征提取，RNN则天然适用于序列数据建模。

三大神经网络预测效果对比

本文行文结构如下：

数据集准备
DNN模型构建及训练
CNN模型构建及训练
RNN模型构建及训练
对比与小结

01 数据集准备

本次实战案例选择了某股票数据，时间范围为2005年1月至2021年7月间的所有交易日，共4027条记录，其中每条记录包含[Open, High, Low, Close, Vol]共5个特征字段。数据示意如下：

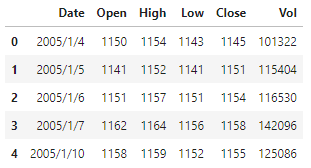
显然，各字段的取值范围不同，为了尽可能适配神经网络中激活函数的最优特性区间，需要对特征字段进行归一化处理，这里选用sklearn中MinMaxScalar进行。同时，为了确保数据预处理时不造成信息泄露，在训练MinMaxScalar时，只能用训练集中的记录。所以，这里按照大体上8:2的比例切分，选择后800条记录用于提取测试集，之前的数据用作训练集。因此，做如下数据预处理：

from sklearn.preprocessing import MinMaxScaler
mms = MinMaxScaler()
mms.fit(df.iloc[:-800][["Open", "High", "Low", "Close", "Vol"]])
df[["Open", "High", "Low", "Close", "Vol"]] = mms.transform(df[["Open", "High", "Low", "Close", "Vol"]])

而后，查看预处理之后的数据：

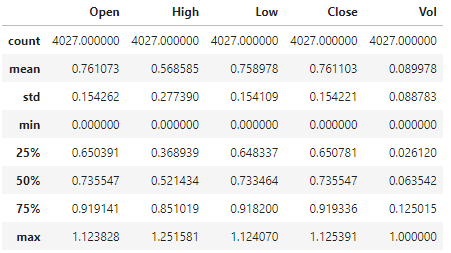
显然，除了Vol列字段的数据范围调整为[0, 1]外，其他4个字段的最大值均超过了1，这是因为测试集中的数据范围比训练集中的数据范围要大，但这更符合实际训练的要求。

而后，进行数据集的构建。既然是时序数据，我们的任务是基于当前及历史一段时间的数据，预测股票次日的收盘价（Close字段），我们大体将历史数据的时间长度设定为30，而后采用滑动窗口的形式依次构建数据集和标签列，构建过程如下：

X = []
y = []
for i in range(30, len(df)):
    X.append(df.iloc[i-30:i, 1:6].values)  # 输入数据未取到i时刻
    y.append(df.iloc[i, 4])  # 标签数据为i时刻
X = torch.tensor(X, dtype=torch.float)
y = torch.tensor(y, dtype=torch.float).view(-1, 1)
X.shape, y.shape
## 输出
(torch.Size([3997, 30, 5]), torch.Size([3997, 1]))

而后，进行训练集和测试集的切分。由于是时序数据，仅能按时间顺序切分，这里沿用之前的设定，及选取后800条记录作为测试集，前面的作为训练集：

N = -800
X_train, X_test = X[:N], X[N:]
y_train, y_test = y[:N], y[N:]
trainloader = DataLoader(TensorDataset(X_train, y_train), 64, True)
X_train.shape, X_test.shape
## 输出
(torch.Size([3197, 30, 5]), torch.Size([800, 30, 5]))

至此，完成了数据集的准备和切分。注意，这里数据集维度为3，其含义为[batch, seq_len, input_size]，即[样本数, 序列长度, 特征数]。接下来开始使用三类神经网络进行建模。

02 DNN模型构建及训练

DNN是最早的神经网络，主要构成元素是若干个全连接层及相应的激活函数。这里为了多个时刻的历史特征一并加入到全连接训练，需要首先对三维的输入数据展平为二维，此处即为[batch, seq_len, input_size]变为[batch, seq_len*input_size]，而后即可应用全连接模块。这里我们对DNN添加3个隐藏层，且遵循神经元数量逐渐减少的节奏。具体来说，DNN模型设计如下：

class ModelDNN(nn.Module):
    def __init__(self, input_size, hiddens=[64, 32, 8]):
        super().__init__()
        self.hiddens = hiddens
        self.net = nn.Sequential(nn.Flatten())
        for pre, nxt in zip([input_size]+hiddens[:-1], hiddens):
            self.net.append(nn.Linear(pre, nxt))
            self.net.append(nn.ReLU())
        self.net.append(nn.Linear(hiddens[-1], 1))
        
    def forward(self, x):
        return self.net(x)

而后即可开始训练，其中模型优化器选择Adam，并保留默认学习率0.001，损失函数选用MSEloss，epoch设置为100，每10个epoch监控一下训练集损失和测试集损失。训练过程如下：

modelDNN = ModelDNN(30*5)
optimizer = optim.Adam(modelDNN.parameters())
criterion = nn.MSELoss()

for i in trange(100):
    for X, y in trainloader:
        y_pred = modelDNN(X)
        loss = criterion(y_pred, y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    if (i+1) % 10 ==0:
        with torch.no_grad():
            train_pred = modelDNN(X_train)
            train_mse = criterion(train_pred, y_train)
            test_pred = modelDNN(X_test)
            test_mse = criterion(test_pred, y_test)
            print(i, train_mse.item(), test_mse.item())
## 输出
9 0.000504376832395792 0.0004596100770868361
19 0.00039938988629728556 0.00026557157980278134
29 0.0003091454564128071 0.00021832890342921019
39 0.0002735845628194511 0.00017248920630663633
49 0.0002678786404430866 0.00018119681044481695
59 0.00024609942920506 0.00013418315211310983                     
69 0.0002652891562320292 0.00018864106095861644
79 0.00023099897953215986 0.00011782139335991815
89 0.000230113830184564 0.0001355513377347961
99 0.00023369801056105644 0.0001391700643580407

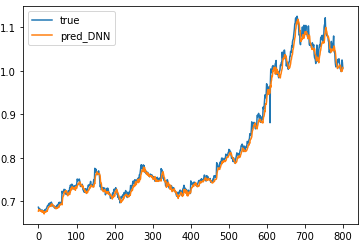
整体来看，模型训练是比较有效的，损失下降得很快。用最终的模型预测一下测试集的输出，并绘制对照曲线：

看上去效果还不错！

03 CNN模型构建及训练

CNN模型的核心元素是卷积和池化，所以这里我们也对该序列数据应用这两个模块。值得注意的是，对于序列数据，特征数应对应卷积核的通道数，而卷积滑动的方向应该是在序列维度上。也就是，此处我们首先应将输入数据形状由[batch, seq_len, input_size]转化为[batch, input_size, seq_len]，而后再应用一维卷积和一维池化层。不失一般性，我们首先设置两个kernel_size=3的Conv1d和两个kernel_size=2的AvgPool1d，而后再将特征展平转变为2维数据，最后经过一个全连接得到预测输出。模型构建代码如下：

class ModelCNN(nn.Module):
    def __init__(self, in_channels, hidden_channels=[8, 4]):
        # input: N x C x L
        # C: 5->8->4
        # L: 30->28->14->12->6
        super().__init__()
        self.in_channels = in_channels
        self.hidden_channels = hidden_channels
        self.net = nn.Sequential()
        for in_channels, out_channels in zip([in_channels]+hidden_channels[:-1], hidden_channels):
            self.net.append(nn.Conv1d(in_channels, out_channels, kernel_size=3))
            self.net.append(nn.AvgPool1d(kernel_size=2))
        self.net.append(nn.Flatten())
        self.net.append(nn.Linear(6*hidden_channels[-1], 1))
        
    def forward(self, x):
        x = x.permute(0, 2, 1)
        return self.net(x)

接下来是训练过程，训练参数沿用DNN中的设定，代码及结果如下：

modelCNN = ModelCNN(5)
optimizer = optim.Adam(modelCNN.parameters())
criterion = nn.MSELoss()

for i in trange(100):
    for X, y in trainloader:
        y_pred = modelCNN(X)
        loss = criterion(y_pred, y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    if (i+1) % 10 ==0:
        with torch.no_grad():
            train_pred = modelCNN(X_train)
            train_mse = criterion(train_pred, y_train)
            test_pred = modelCNN(X_test)
            test_mse = criterion(test_pred, y_test)
            print(i, train_mse.item(), test_mse.item())
## 输出
9 0.0006343051209114492 0.0005071654450148344
19 0.0005506690358743072 0.0005008925218135118
29 0.00048158588469959795 0.0003848765918519348
39 0.0004702212754637003 0.00034184992546215653
49 0.00042759429197758436 0.00038456765469163656
59 0.0003927639627363533 0.00028791968361474574
69 0.00037852991954423487 0.0002683571365196258
79 0.00034848105860874057 0.00025418962468393147
89 0.00035096638021059334 0.00023561224224977195
99 0.0003425602917559445 0.00022362983145285398

绘图展示一下：

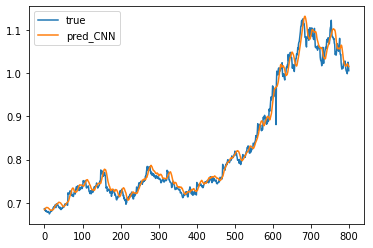
看上去效果也不错！

04 RNN模型构建及训练

RNN是天然适用于序列数据建模的，这里我们选用GRU实践一下，并只选择最基础的GRU结构，即num_layers=1，bidirectional=False。在最后时刻输出的隐藏状态hn的基础上，使用一个全连接得到预测输出。网络结构代码如下：

class ModelRNN(nn.Module):
    def __init__(self, input_size, hidden_size):
        super().__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        
        # 注意，这里设置batch_first=True
        self.gru = nn.GRU(input_size=input_size, hidden_size=hidden_size, batch_first=True)
        self.activation = nn.ReLU()
        self.output = nn.Linear(hidden_size, 1)
        
    def forward(self, x):
        _, hidden = self.gru(x)
        hidden = hidden.squeeze(0)
        hidden = self.activation(hidden)
        return self.output(hidden)

RNN模型训练仍沿用前序训练参数设定，训练过程及结果如下：

modelRNN = ModelRNN(5, 4)
optimizer = optim.Adam(modelRNN.parameters())
criterion = nn.MSELoss()

for i in trange(100):
    for X, y in trainloader:
        y_pred = modelRNN(X)
        loss = criterion(y_pred, y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    if (i+1) % 10 ==0:
        with torch.no_grad():
            train_pred = modelRNN(X_train)
            train_mse = criterion(train_pred, y_train)
            test_pred = modelRNN(X_test)
            test_mse = criterion(test_pred, y_test)
            print(i, train_mse.item(), test_mse.item())
## 输出
9 0.00942652765661478 0.014085204340517521
19 0.0008321275236085057 0.003637362737208605
29 0.0002676403964869678 0.001723079476505518
39 0.00024218574981205165 0.0013364425394684076
49 0.00022829060617368668 0.0011184979230165482
59 0.0002223998453700915 0.0009826462483033538
69 0.00021638070757035166 0.0008919781539589167
79 0.00021416762319859117 0.0008065822767093778
89 0.00022308445477392524 0.0007256607641465962
99 0.00021087308414280415 0.0006862917798571289

查看一下输出，并绘制预测结果曲线如下：

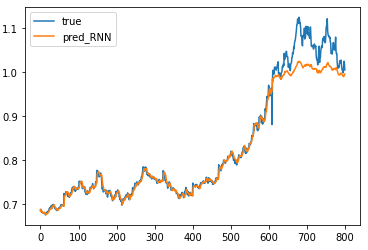
前面预测的都还是比较准的，只是最后一点预测误差较大，这可能是由于测试集标签真实值超出了1，而这种情况是模型在训练集上所学不到的信息……

05 对比与小结

最后，我们综合对比一下三大神经网络模型在该股票预测任务上的表现。首先来看各自的预测结果对比曲线：

整体来看，DNN和CNN在全部测试集上的表现要略胜于RNN一些。然后再从评价指标和训练速度方面对比一下：

好吧，DNN几乎呈现碾压态势——模型训练速度快，预测结果精度高！这大体可以体现两个结论：

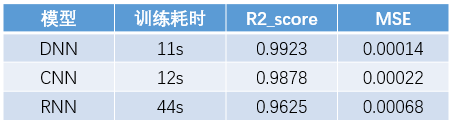
机器学习界广泛受用的“天下没有免费的午餐”定理，即不存在一种确切的模型在所有数据集上均表现较好；
虽然RNN是面向序列数据建模而生，但DNN和CNN对这类任务也有一定的适用性，巧妙设计网络结构也能带来不错的效果。

以上案例及结论仅供参考！