神经网络实验代码 | PyTorch系列（二十七）-技术圈

点击上方“AI算法与图像处理”，选择加"星标"或“置顶”

重磅干货，第一时间送达

文 |AI_study

原标题：Training Loop Run Builder - Neural Network Experimentation Code

使用RunBuilder类

本文以及本系列最后几节的目的是使自己处于能够有效地尝试我们所构建的训练过程的位置。因此，我们将扩展在超参数实验中该情节涉及的内容。我们将使那里看到的更加干净。

我们将构建一个名为RunBuilder的类。但是，在介绍如何构建类之前。让我们看看它将允许我们做什么。我们将从import 开始。

from collections import OrderedDictfrom collections import namedtuplefrom itertools import product

我们正在从 collections 中导入OrderedDict和namedtuple，并且正在从itertools中导入一个名为product的函数。这个product（）函数是我们上次看到的函数，它在给定多个列表输入的情况下计算笛卡尔乘积。

好的。这是RunBuilder类，它将构建用于定义运行的参数集。看到如何使用后，我们将看到它的工作原理。

class RunBuilder():    @staticmethod    def get_runs(params):
        Run = namedtuple('Run', params.keys())
        runs = []        for v in product(*params.values()):            runs.append(Run(*v))
        return runs

关于使用此类的主要注意事项是它具有一个称为get_runs（）的静态方法。该方法将为我们提供基于传入参数构建的运行结果。

现在定义一些参数。

params = OrderedDict(                lr = [.01, .001],            batch_size = [1000, 10000])

在这里，我们在字典中定义了一组参数和值。我们有一组要尝试的学习率和一组批batch的大小。当我们说“尝试”时，是指我们要针对字典中的每个学习率和每个批次大小进行一次训练。

要获得这些运行，我们只需调用RunBuilder类的get_runs（）函数，并传入我们要使用的参数即可。

> runs = RunBuilder.get_runs(params)> runs
[    Run(lr=0.01, batch_size=1000),    Run(lr=0.01, batch_size=10000),    Run(lr=0.001, batch_size=1000),    Run(lr=0.001, batch_size=10000)]

很好，我们可以看到RunBuilder类已经构建并返回了四个运行的列表。这些运行中的每一个都有学习率和定义运行的batch大小。

我们可以通过索引到列表来访问单个运行，如下所示：

> run = runs[0]> run
Run(lr=0.01, batch_size=1000)

注意运行输出的字符串表示形式。此字符串表示形式是由Run tuple类为我们自动生成的，如果我们想将运行统计信息写到TensorBoard或任何其他可视化程序的磁盘上，则可以使用该字符串唯一标识运行。

另外，由于run is object是具有命名属性的元组，因此我们可以使用点表示法访问值，如下所示：

> print(run.lr, run.batch_size)
0.01 1000

最后，由于运行列表是Python可迭代的，因此我们可以像这样干净地迭代运行：

for run in runs:    print(run, run.lr, run.batch_size)

输出：

Run(lr=0.01, batch_size=1000) 0.01 1000Run(lr=0.01, batch_size=10000) 0.01 10000Run(lr=0.001, batch_size=1000) 0.001 1000Run(lr=0.001, batch_size=10000) 0.001 10000

要添加其他值，我们要做的就是将它们添加到原始参数列表中，如果我们想添加其他类型的参数，我们要做的就是添加它。新参数及其值将自动变为可在运行中使用。运行的字符串输出也将更新。

两个参数：

params = OrderedDict(    lr = [.01, .001]    ,batch_size = [1000, 10000])
runs = RunBuilder.get_runs(params)runs

输出：

[    Run(lr=0.01, batch_size=1000),    Run(lr=0.01, batch_size=10000),    Run(lr=0.001, batch_size=1000),    Run(lr=0.001, batch_size=10000)]

三个参数：

params = OrderedDict(    lr = [.01, .001]    ,batch_size = [1000, 10000]    ,device = ["cuda", "cpu"])
runs = RunBuilder.get_runs(params)runs

输出：

[    Run(lr=0.01, batch_size=1000, device='cuda'),    Run(lr=0.01, batch_size=1000, device='cpu'),    Run(lr=0.01, batch_size=10000, device='cuda'),    Run(lr=0.01, batch_size=10000, device='cpu'),    Run(lr=0.001, batch_size=1000, device='cuda'),    Run(lr=0.001, batch_size=1000, device='cpu'),    Run(lr=0.001, batch_size=10000, device='cuda'),    Run(lr=0.001, batch_size=10000, device='cpu')]

当我们在训练过程中尝试不同的值时，此功能将使我们能够更好地控制。

让我们看看如何构建此RunBuilder类。

编码 RunBuilder类

我们需要具备的第一件事就是我们想要尝试的参数和值字典。

params = OrderedDict(    lr = [.01, .001]    ,batch_size = [1000, 10000])

接下来，我们从字典中获得键列表。

> params.keys()odict_keys(['lr', 'batch_size'])

然后，我们从字典中获取值列表。

> params.values()odict_values([[0.01, 0.001], [1000, 10000]])

有了这两个功能之后，我们只需检查一下它们的输出，以确保我们了解它们。完成后，我们将使用这些键和值进行下一步操作。我们将从键开始。

Run = namedtuple('Run', params.keys())

该行创建一个名为Run的新元组子类，该子类具有命名字段。这个Run类用于封装每次运行的数据。此类的字段名称由传递给构造函数的名称列表设置。首先，我们传递类名。然后，我们传递字段名，在本例中，我们传递字典中的键列表。

现在我们有了一个用于运行的类，我们准备创建一些类。

runs = []for v in product(*params.values()):    runs.append(Run(*v))

首先，我们创建一个名为runs的列表。然后，我们使用itertools中的product（）函数使用字典中每个参数的值来创建笛卡尔乘积。这给了我们一组定义运行的有序对。我们遍历所有这些，将运行添加到每个运行的列表中。

对于笛卡尔乘积中的每个值，我们都有一个有序的元组。笛卡尔积为我们提供了每个订购对，因此我们拥有所有可能的订购对，其学习率和批量大小均如此。当将元组传递给Run构造函数时，我们使用*运算符告诉构造函数接受元组值作为与元组本身相反的参数。

最后，我们将此代码包装在RunBuilder类中。

class RunBuilder():    @staticmethod    def get_runs(params):
        Run = namedtuple('Run', params.keys())
        runs = []        for v in product(*params.values()):        runs.append(Run(*v))
        return runs

由于get_runs（）方法是静态的，因此我们可以使用类本身来调用它。我们不需要该类的实例。

现在，这使我们可以通过以下方式更新我们的训练代码：

之前：

for lr, batch_size, shuffle in product(*param_values):    comment = f' batch_size={batch_size} lr={lr} shuffle={shuffle}'
    # Training process given the set of parameters

之后

for run in RunBuilder.get_runs(params):    comment = f'-{run}'        # Training process given the set of parameters

什么是笛卡尔积？

您知道笛卡尔积吗？像生活中的许多事物一样，笛卡尔积是一个数学概念。笛卡尔积是二进制运算。该操作将两组作为参数，并返回第三组作为输出。让我们看一个通用的数学示例。

假设 X 是一个集合。

假设 Y 是一个集合。

两组之间的笛卡尔积表示为：X * Y。集合X和集合Y的笛卡尔积被定义为所有有序对的集合对（x, y）, x∈X 和 y∈Y。这可以用以下方式表示：

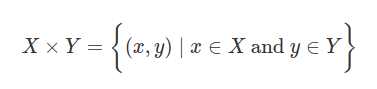
这种表示笛卡尔乘积的输出的方式称为集合生成器符号。很酷。所以X *Y 是所有有序对的集合（x, y）, x∈X 和 y∈Y。

计算X*Y

我们执行以下操作：对于每个x∈X 和 y∈Y，我们收集相应的对（x, y）。结果集合给我们的是所有有序对的集合

这是用Python表达的具体示例：

X = {1,2,3}Y = {1,2,3}
{ (x,y) for x in X for y in Y }

输出：

{(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}

注意数学代码是多么强大。它包括所有的情况。也许你注意到这可以通过使用for循环迭代来实现，就像这样:

X = {1,2,3}Y = {1,2,3}cartesian_product = set()for x in X:    for y in Y:        cartesian_product.add((x,y))cartesian_product

输出：

{(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}

结束好了，现在我们知道它是如何工作的了，我们可以继续使用它。

文章中内容都是经过仔细研究的，本人水平有限，翻译无法做到完美，但是真的是费了很大功夫，希望小伙伴能动动你性感的小手，分享朋友圈或点个“在看”，支持一下我 ^_^

英文原文链接是：

https://deeplizard.com/learn/video/NSKghk0pcco

加群交流

欢迎小伙伴加群交流，目前已有交流群的方向包括：AI学习交流群，目标检测，秋招互助，资料下载等等；加群可扫描并回复感兴趣方向即可（注明：地区+学校/企业+研究方向+昵称）

谢谢你看到这里！ 👇