用 Python 绘制一个 Facebook 元宇宙新 Logo
Facebook 为了投身元宇宙,连名字都改了 Meta,也更换了 LOGO。

但这个 LOGO 似乎不是艺术家凭感觉设计的,而是有来头的,在数学上称为 Lissajous 曲线。
平面上的 Lissajous 曲线可以看成是沿着相互垂直方向的两个正弦振动的合成,具体是由以下参数方程描述的一系列曲线:
Lissajous 曲线在物理学、天文学和其他科学中都有应用。下面是一些 Lissajous 曲线示例,你可以通过更改 Python 代码中常量 A 和 B 的值,塑造出更多的具体曲线。
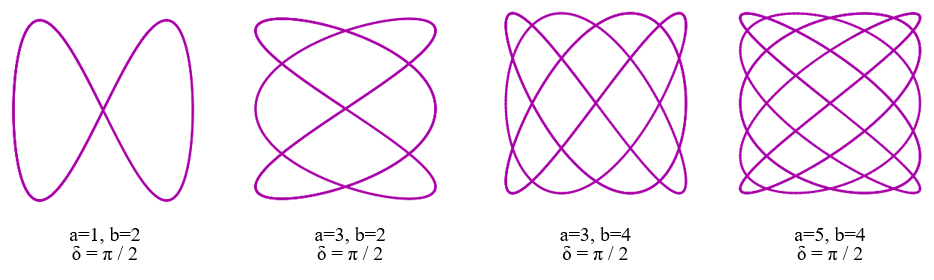
下面就让我们用 Python 来试着绘制一下这个 LOGO。
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.style.use('Solarize_Light2')
import seaborn as sns
sns.set_style("white")
所谓参数曲线,就是要根据参数来确定曲线上的每一个点。也就是说在绘制时,我们需要根据参数来取不同点的
设置常量参数 、 、 、 以及 ,控制曲线整体的形状。
A, B = 1, 1
delta = 3.14159/2
设置曲线上采样点的参数向量 。我们先取 50 个点,便于观察点在曲线上的分布。
t = np.linspace(0, 2*np.pi, 50)
fig = plt.figure(figsize=(8,4.5))
a = 1
b = 2
x = A * np.sin(a*t + delta)
y = B * np.sin(b*t)
plt.plot(x, y, '-o');
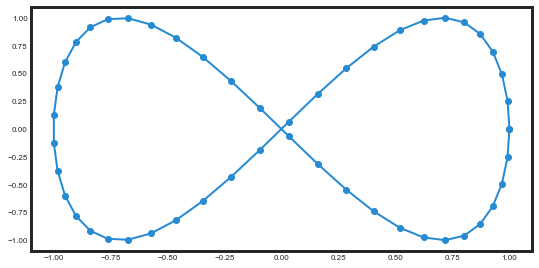
这画出来了一个无穷大
我们不妨将上述内容写在一起,定义一个简单的函数,方便后面调用。
def drawLissajous2D(r=10,n=500,A=1,B=1,a=1,b=1,delta=1.75,lw=2):
t = np.linspace(0, r, n)
fig = plt.figure(figsize=(8,4.5))
x = A * np.sin(a*t + delta)
y = B * np.sin(b*t)
plt.plot(x, y, '-',linewidth=lw)
为了更方便观察曲线上绘制的点列,我们将参数
t = np.linspace(0, np.pi, 50)
fig = plt.figure(figsize=(8,4.5))
a = 1
b = 2
x = A * np.sin(a*t + delta)
y = B * np.sin(b*t)
plt.plot(x, y, '-o');
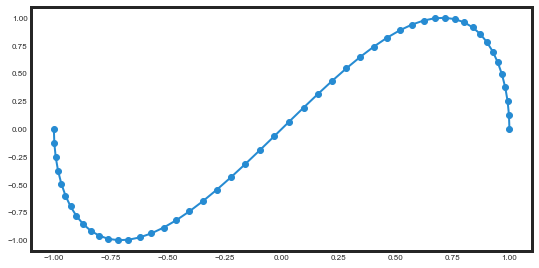
上面只看到了无穷大的一半,因为只画了半个周期。把这些点想象成动点,将其两个坐标分开考虑,
取 500 个点,调整下 和 的值,再次绘制曲线。曲线的样子是不是改变了,上下并不对称了。
drawLissajous2D(n=500,a=1,b=2)

调整常量参数以及线条的宽度
drawLissajous2D(n=500,a=1,b=2,lw=12)

看看其他参数画出来的是个啥?
drawLissajous2D(n=300,a=1,b=1,delta=3.14159/2,lw=6)

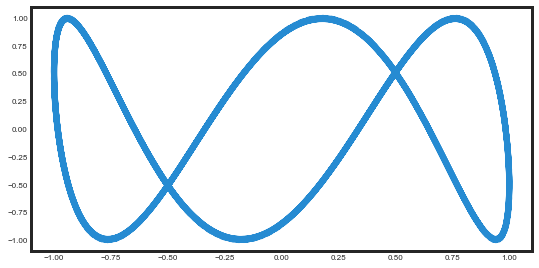
drawLissajous2D(n=300,a=3,b=9,lw=6)
13D 版本
还可以二维版本的 Lissajous 曲线扩展到三维空间中,得到三维版本的空间 Lissajous 曲线。只要增加一个
from mpl_toolkits import mplot3d
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc('xtick', labelsize=8)
matplotlib.rc('ytick', labelsize=8)
def drawLissajous3D(r=2*np.pi,n=500,A=1,B=1,C=1,a=1,b=1,c=2,delta=1.75,epsilon=1.75):
# 设置 Lissajous 参数。
t = np.linspace(0, r, n)
x = A * np.sin(a*t)
y = B * np.sin(b*t + delta)
z = C * np.sin(c*t + epsilon)
plt.figure(figsize=(8,6))
ax = plt.axes(projection='3d')
ax.plot3D(x, y, z, '-', linewidth=6)
ax.set_xlabel('$x = A sin(at)$', fontsize=12)
ax.set_ylabel('$y = B sin(bt + \delta)$', fontsize=12)
ax.set_zlabel('$z = C sin(ct + \epsilon)$', fontsize=12)
plt.title("Lissajous 3D Curve", fontsize=12)
ax.view_init(2, 60)
drawLissajous3D()

可以在窗口中用鼠标交互,比如转动看看,

如果有兴趣,可以将上述绘制改成旋转动画,让这个 LOGO 在三维空间中动起来哦。
评论
