用 Python 绘制图表理解神经网络

人工神经网络 (ANN) 已成功应用于许多需要人工监督的日常任务,但由于其复杂性,很难理解它们的工作方式和训练方式。
在这篇博客中,我们深入讨论了神经网络是什么、它们是如何工作的,以及如何将它们应用于诸如寻找异常值或预测金融时间序列之类的问题。
在这篇文章中,我尝试直观地展示一个简单的前馈神经网络如何在训练过程中将一组输入映射到不同的空间,以便更容易理解它们。
数据
为了展示它是如何工作的,首先我创建了一个“ toy”数据集。它包含 400 个均匀分布在两个类(0 和 1)中的样本,每个样本具有两个维度(X0 和 X1)。
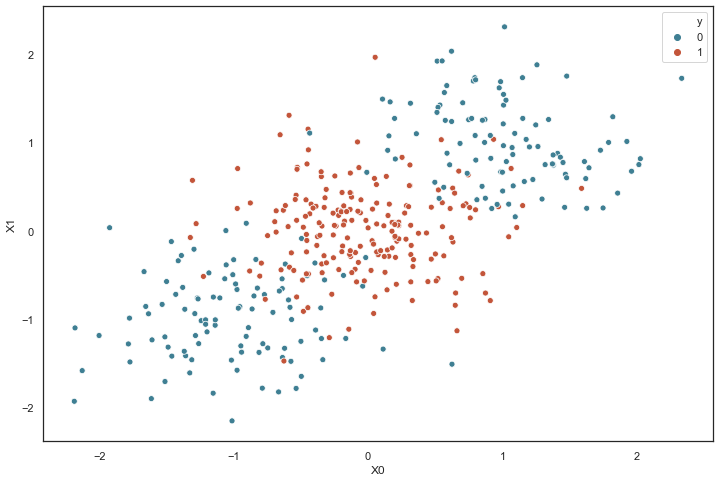
注:所有数据均来自三个随机正态分布,均值为 [-1, 0, 1],标准差为 [0.5, 0.5, 0.5]。
网络架构
下一步是定义ANN的结构,如下:
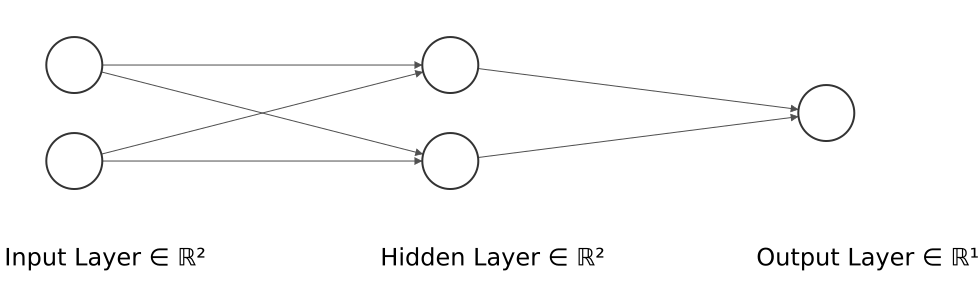
隐藏层的维度最小(2 个神经元)以显示网络在 2D 散点图中映射每个样本的位置。
尽管前面的图表没有显示,但每一层都有一个修改其输出的激活函数。
•输入层有一个linear激活函数来复制它的输入值。
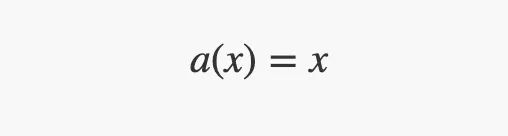
•隐藏层具有ReLU或tanh激活函数。
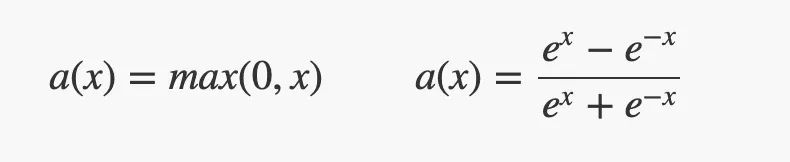
•输出层有一个sigmoid激活函数,可以将其输入值“缩小”到 [0, 1] 范围内。
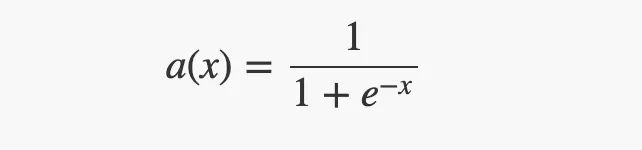
训练
除了网络的架构之外,神经网络的另一个关键方面是训练过程。训练 ANN 的方法有很多种,但最常见的是反向传播过程。
反向传播过程首先将所有训练案例(或一批)前馈到网络,然后优化器根据损失函数计算“如何”更新网络的权重,并根据学习率更新它们。
当损失收敛、经过一定数量的 epoch 或用户停止训练时,训练过程停止。一个epoch 表示所有的数据送入网络中, 完成了一次前向计算 + 反向传播的过程。
在我们的研究案例中,该架构使用隐藏层中的 2 个不同激活函数(ReLU 和 Tanh)和 3 个不同的学习率(0.1、0.01 和 0.001)进行训练。
在输入样本周围,有一个“网格”点,显示模型为该位置的样本提供的预测概率。这使得模型在训练过程中生成的边界更加清晰。
# figure holding the evolutionf, axes = plt.subplots(1, 3, figsize=(18, 6), gridspec_kw={'height_ratios':[.9]})f.subplots_adjust(top=0.82)# camera to record the evolutioncamera = Camera(f)# number of epochsepochs = 20# iterate epoch timesfor i in range(epochs):# evaluate the model (acc, loss)evaluation = model.evaluate(x_train, y_train, verbose=0)# generate intermediate modelsmodel_hid_1 = Model(model.input, model.get_layer("hidden_1").output)model_act_1 = Model(model.input, model.get_layer("activation_1").output)# generate datadf_hid_1 = pd.DataFrame(model_hid_1.predict(x_train), columns=['X0', 'X1'])df_hid_1['y'] = y_traindf_act_1 = pd.DataFrame(model_act_1.predict(x_train), columns=['X0', 'X1'])df_act_1['y'] = y_train# generate meshgrid (200 values)x = np.linspace(x_train[:,0].min(), x_train[:,0].max(), 200)y = np.linspace(x_train[:,1].min(), x_train[:,1].max(), 200)xv, yv = np.meshgrid(x, y)# generate meshgrid intenistydf_mg_train = pd.DataFrame(np.stack((xv.flatten(), yv.flatten()), axis=1), columns=['X0', 'X1'])df_mg_train['y'] = model.predict(df_mg_train.values)df_mg_hid_1 = pd.DataFrame(model_hid_1.predict(df_mg_train.values[:,:-1]), columns=['X0', 'X1'])df_mg_hid_1['y'] = model.predict(df_mg_train.values[:,:-1])df_mg_act_1 = pd.DataFrame(model_act_1.predict(df_mg_train.values[:,:-1]), columns=['X0', 'X1'])df_mg_act_1['y'] = model.predict(df_mg_train.values[:,:-1])# show datasetax = sns.scatterplot(x='X0', y='X1', data=df_mg_train, hue='y', x_jitter=True, y_jitter=True, legend=None, ax=axes[0], palette=sns.diverging_palette(220, 20, as_cmap=True), alpha=0.15)ax = sns.scatterplot(x='X0', y='X1', data=df_train, hue='y', legend=None, ax=axes[0], palette=sns.diverging_palette(220, 20, n=2))ax.set_title('Input layer')ax = sns.scatterplot(x='X0', y='X1', data=df_mg_hid_1, hue='y', x_jitter=True, y_jitter=True, legend=None, ax=axes[1], palette=sns.diverging_palette(220, 20, as_cmap=True), alpha=0.15)ax = sns.scatterplot(x='X0', y='X1', data=df_hid_1, hue='y', legend=None, ax=axes[1], palette=sns.diverging_palette(220, 20, n=2))ax.set_title('Hidden layer')# show the current epoch and the metricsax.text(x=0.5, y=1.15, s='Epoch {}'.format(i+1), fontsize=16, weight='bold', ha='center', va='bottom', transform=ax.transAxes)ax.text(x=0.5, y=1.08, s='Accuracy {:.3f} - Loss {:.3f}'.format(evaluation[1], evaluation[0]), fontsize=13, ha='center', va='bottom', transform=ax.transAxes)ax = sns.scatterplot(x='X0', y='X1', data=df_mg_act_1, hue='y', x_jitter=True, y_jitter=True, legend=None, ax=axes[2], palette=sns.diverging_palette(220, 20, as_cmap=True), alpha=0.15)ax = sns.scatterplot(x='X0', y='X1', data=df_act_1, hue='y', legend=None, ax=axes[2], palette=sns.diverging_palette(220, 20, n=2))ax.set_title('Activation')# show the plotplt.show()# call to generate the GIFcamera.snap()# stop execution if loss <= 0.263 (avoid looping 200 times if not needed)if evaluation[0] <= 0.263:break# train the model 1 epochmodel.fit(x_train, y_train, epochs=1, verbose=0)
ReLU 激活
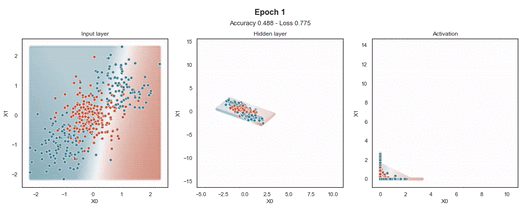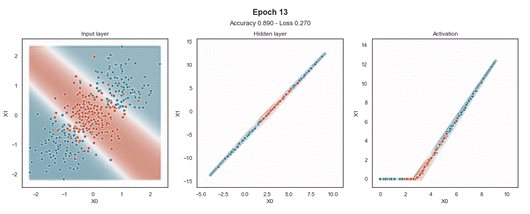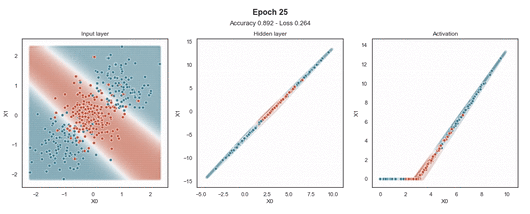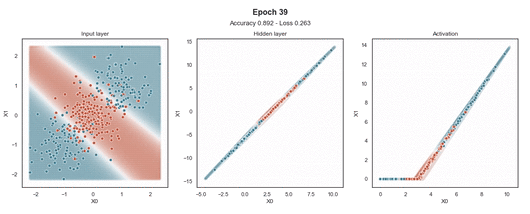
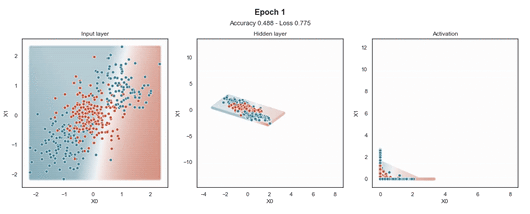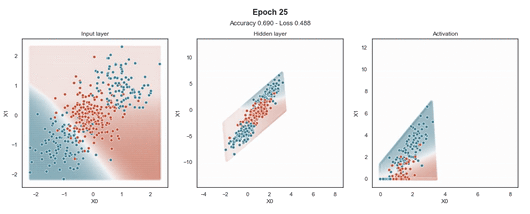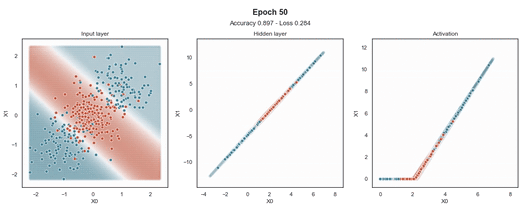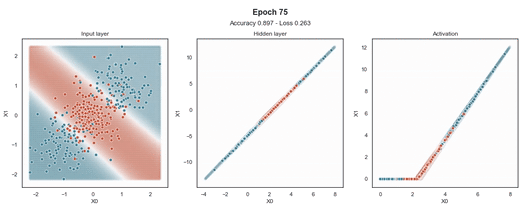
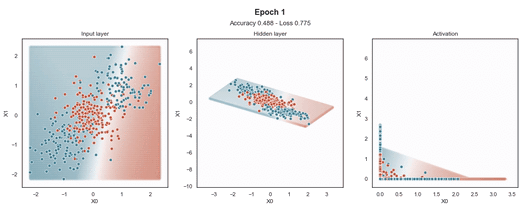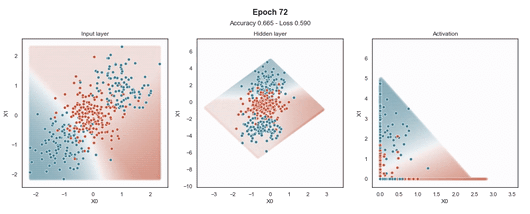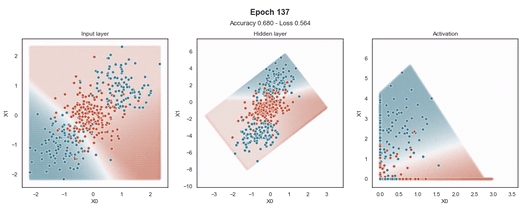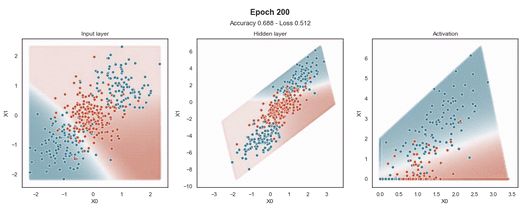
Tanh 激活
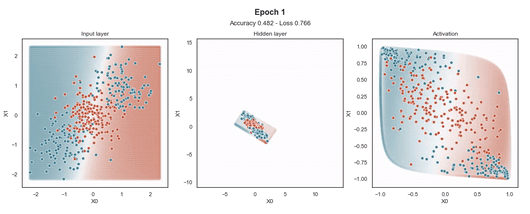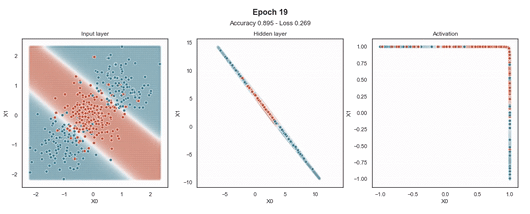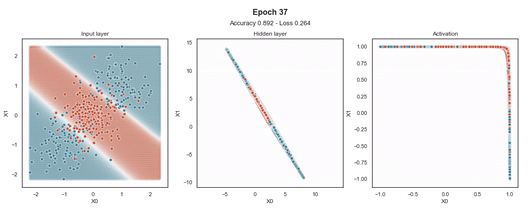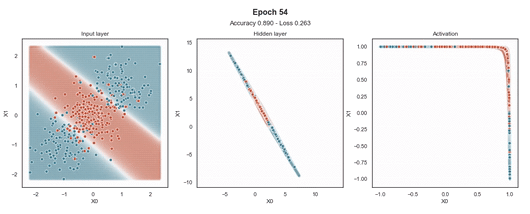
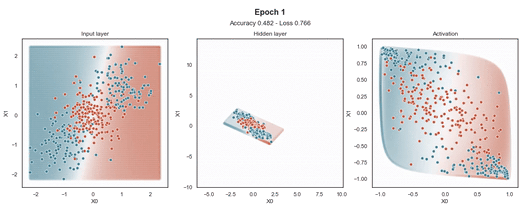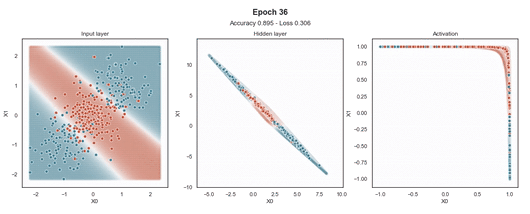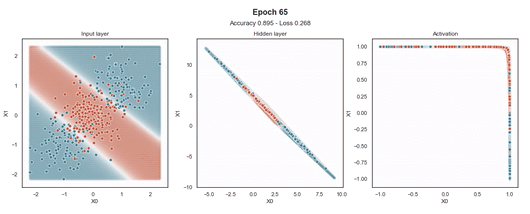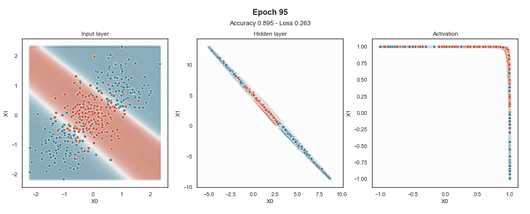
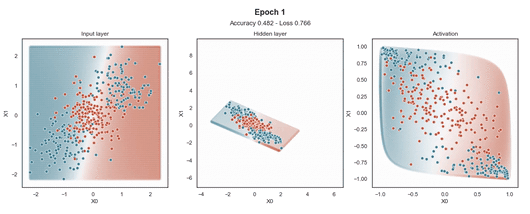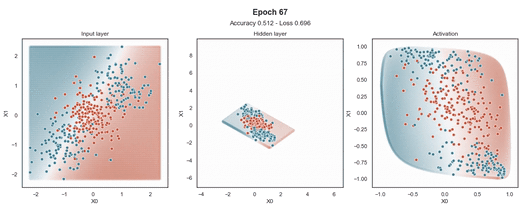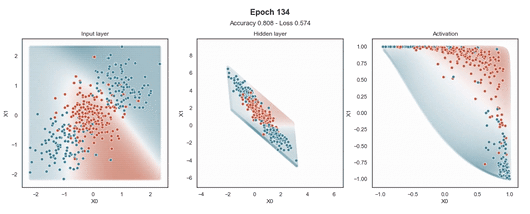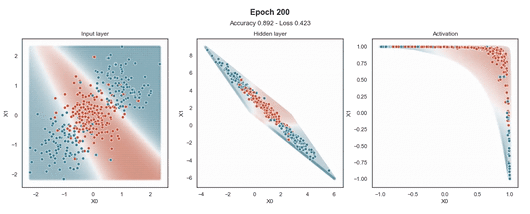
注意:使用的损失函数是二元交叉熵,因为我们正在处理二元分类问题,而优化器是对原始随机梯度下降 (SGD) 称为 Adam 的修改。当epoch达到 200 或损失低于 0.263 时,模型训练停止。
