本文为大家梳理了相关分析的生活实例、原理、方法、误区，欢迎留言一起探讨。

Part1什么是相关性

“万物皆有联”，是大数据一个最重要的核心思维。

所谓联，这里指的就是事物之间的相互影响、相互制约、相互印证的关系。而事物这种相互影响、相互关联的关系，在统计学上就叫做相关关系，简称相关性。

世界上的所有事物，都会受到其它事物的影响：

• HR经常会问：影响员工离职的关键原因是什么？是工资还是发展空间？

• 销售人员会问：哪些要素会促使客户购买某产品？是价格还是质量？

• 营销人员会问：影响客户流失的关键因素有哪些？是竞争还是服务等？

• 产品设计人员：影响汽车产品受欢迎的关键功能有哪些？价格、还是动力等？

所有的这些商业问题，转化为数据问题，不外乎就是评估一个因素与另一个因素之间的相互影响或相互关联的关系。而分析这种事物之间关联性的方法，就是相关性分析方法。

当然，有相关关系，并不一定意味着是因果关系。但因果关系，则一定是相关关系。

在过去，传统的统计模型主要是用来寻找影响事物的因果关系，所以过去也叫影响因素分析。但是，从统计学方法来说，因果关系一定会有统计显著，但统计显著并不一定就是因果关系，所以准确地说，影响因素分析应该改为相关性分析。

所以，在不引起混淆的情况下，我们也会用影响因素分析。

Part2相关性与影响因素分析

1相关性种类

客观事物之间的相关性，大致可归纳为两大类：一类是函数关系，一类是统计关系。

• 函数关系，就是两个变量的取值存在一个函数关系来唯一描述。比如，销售额与销售量之间的关系，可用函数y=px（y表示销售额，p表示单价，x表示销售量）来表示。所以，销售量和销售额存在函数关系。这一类确定性的关系，不是我们关注的重点。

• 统计关系，指的是两事物之间的非一一对应关系，即当变量x取一定值时，另一个变量y虽然不唯一确定，但按某种规律在一定的可预测范围内发生变化。比如，子女身高与父母身高、广告费用与销售额的关系，是无法用一个函数关系唯一确定其取值的，但这些变量之间确实存在一定的关系。大多数情况下，父母身高越高，子女的身高也就越高；广告费用花得越多，其销售额也相对越多。这种关系，就叫做统计关系。

进一步，统计分析如果按照相关的形态来说，可分为线性相关和非线性相关（曲线相关）；如果按照相关的方向来分，可分为正相关和负相关，等等。详细见下面的图形。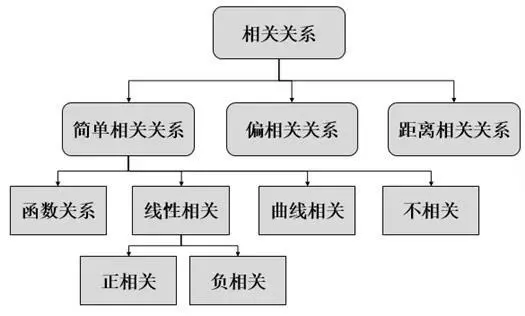

2相关性描述方式

描述两个变量是否有相关性，常见的方式有：可视化相关图（典型的如散点图和列联表等等）、相关系数、统计显著性。

如果用可视化的方式来呈现各种相关性，常见有如下散点图：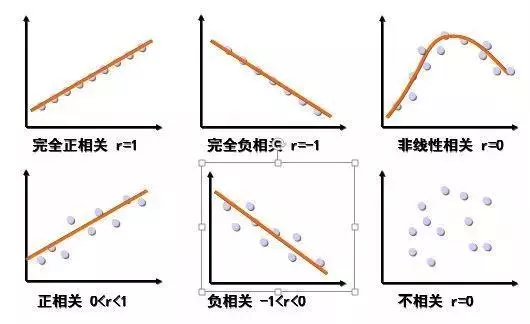

3相关性方法种类

对于不同的因素类型，采用的相关性分析方法也不相同。

下面简单总结一下所选用的相关性分析方法：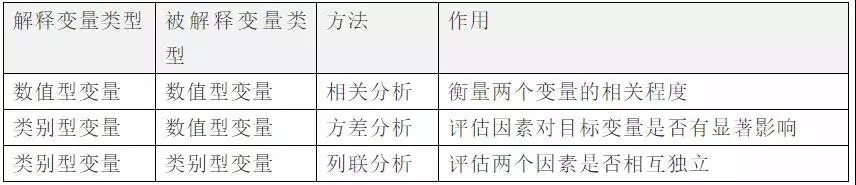

Part3相关分析主要方法

简单地说，相关分析，就是衡量两个数值型变量的相关性，以及计算相关程度的大小。

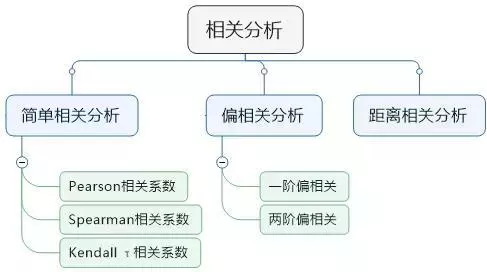
4相关分析种类

相关分析，常用的方法类别有：简单相关分析、偏相关分析、距离相关分析等。其中前两种方法比较常见。

• 简单相关分析，是直接计算两个变量的相关程度。

• 偏相关分析，是在排除某个因素后，两个变量的相关程度。

• 距离相关分析，是通过两个变量之间的距离来评估其相似性（这个少用）。

5散点图

判断两个变量是否存在线性相关关系，一种最简单的方法就是可视化。

相关分析中最合适的图形就是散点图。在下表中，将腰围、脂肪比重和体重用散点图的方式画出来，则如下图所示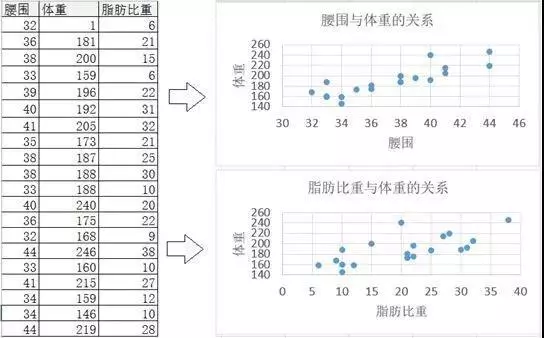：显然，随着腰围的增加，体重也在增加。说明，腰围和体重是存在相关关系的，而且应该是正相关。同样，脂肪比重与体重也是正相关的。

可视化的优点是：直观，但其缺点是：无法准确度量。比如腰围和脂肪比重，对体重的影响程度到底有多大？或者说，这两个因素中哪个因素对体重的影响会更大？散点图是无法给出答案的（所以，我们接下来要引入更强大的方法）。

所以，在相关分析时，我们将引入一个新的数据指标（即相关系数），专门用于衡量两个变量的线性相关程度。

6相关系数

相关系数（CorrelationCoefficient），是专门用来衡量两个变量之间的线性相关程度的指标，经常用字母r来表示相关系数。

相关系数，是以数值的方式来精确地反映两个变量之间线性相关的强弱程度的。最常用的相关系数，是皮尔逊（Pearson）相关系数，又称积差相关系数，公式如下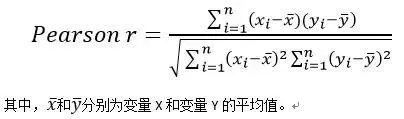：相关系数的特征如下：

• 相关系数的取值范围是在[-1，1]之间。

• |r|越趋于1，表示线性相关越强；|r|越趋于0，表示线性相关越弱。

• 若|r|=1，为完全线性相关（相当于两变量有函数关系）

• r=1，为完全正线性相关。

• r=-1，为完全负线性相关。

• 若r >0，表示两个变量存在正相关。

• 若r< 0，表示两个变量存在负相关。

• 若r = 0，表示两个变量不存在线性相关关系。

其实，并不是说一定要r=0时才表示两变量不存在线性相关。在实际的应用中，因为r表示的是相关程度，所以我们往往会将r的取值分成几个区间，来表示不同的相关程度（如下图所示）:显著性检验

由于上述相关系数是根据样本数据计算出来的，所以上述相关系数又称为样本相关系数（用r来表示）。若相关系数是根据总体全部数据计算的，称为总体相关系数，记为ρ。

但由于存在抽样的随机性和样本较少等原因，通常样本相关系数不能直接用来说明两总体（即两变量）是否具有显著的线性相关关系，因此还必须进行显著性检验。相关分析的显著性检验，经常使用假设检验的方式对总体的显著性进行推断。

显著性检验的步骤如下：

假设：两个变量无显著性线性关系，即两个变量存在零相关。

构建新的统计量t，如下所示

由于上述相关系数是根据样本数据计算出来的，所以上述相关系数又称为样本相关系数（用r来表示）。若相关系数是根据总体全部数据计算的，称为总体相关系数，记为ρ。

但由于存在抽样的随机性和样本较少等原因，通常样本相关系数不能直接用来说明两总体（即两变量）是否具有显著的线性相关关系，因此还必须进行显著性检验。相关分析的显著性检验，经常使用假设检验的方式对总体的显著性进行推断。

显著性检验的步骤如下：

假设：两个变量无显著性线性关系，即两个变量存在零相关。

构建新的统计量t，如下所示: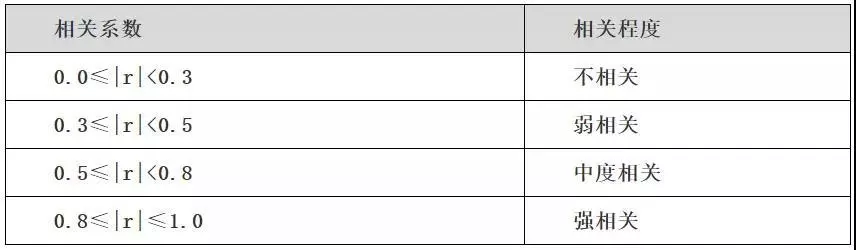

7显著性检验

由于上述相关系数是根据样本数据计算出来的，所以上述相关系数又称为样本相关系数（用r来表示）。若相关系数是根据总体全部数据计算的，称为总体相关系数，记为ρ。

但由于存在抽样的随机性和样本较少等原因，通常样本相关系数不能直接用来说明两总体（即两变量）是否具有显著的线性相关关系，因此还必须进行显著性检验。相关分析的显著性检验，经常使用假设检验的方式对总体的显著性进行推断。

显著性检验的步骤如下：

1. 假设：两个变量无显著性线性关系，即两个变量存在零相关。

2. 构建新的统计量t，如下所示:

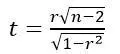
• 在变量X和Y服从正态分布时，该t统计量服从自由度为n-2的t分布。

• 计算统计量t，并查询t分布对应的概率P值。

• 最后判断（α表示显著性水平，一般取0.05）：

  1）如果P<α，表示两变量存在显著的线性相关关系；

  2）否则，不存在显著的线性相关关系。

Part4相关分析基本步骤

简单相关分析的基本步骤如下：下面以腰围、体重、脂肪比重为例，来说明应该怎样进行相关分析。

第1步：绘制散点图

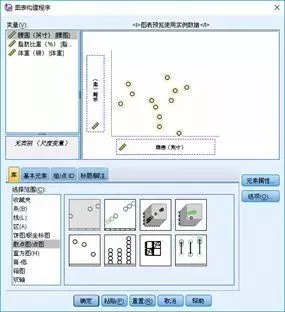
在SPSS中，绘制散点图非常简单。操作步骤如下：

1. 点击【图形- 图表】构建程序。

2. 在库中选择散点图，双击简单散点图。

3. 分别将腰围和体重，拖入X轴和Y轴，确定即可。

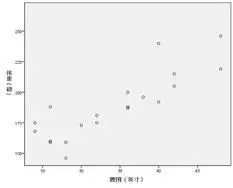
观察散点图，可知：腰围与体重应该是存在线性相关性的，或者说，腰围对体重是有影响的。不过，这相关程度（或影响程度）有多大，则需要进一步计算相关系数来度量。

第2步：选择系数公式

因为，Pearson相关系数要求变量服从正态分布，所以在计算相关系数之前，需要先确定两变量是否都服从正态分布，或者近似正态分布。如果采用其它相关系数（参考“相关系数种类”小节），则可以省略正态性检验。

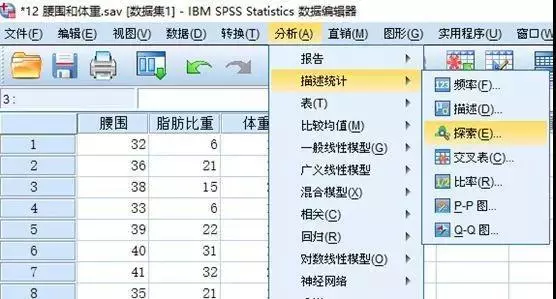
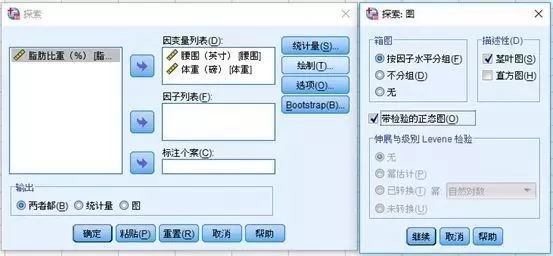
在SPSS中，判断两变量是否服从正态分布操作步骤如下：

1. 点击【分析 - 描述统计 - 探索】，进入探索界面。

2. 将待判断的变量选入因变量列表。

3. 打开绘制界面，选中带检验的正态图，确定。确定后得到如下的正态性检验结果：在SPSS中，采用的是K-S检验以及Shapiro-Wilk检验的结果。当Sig>0.05时，表明该变量服从正态分布，否则为非正态分布。

注：当样本量大于50时用K-S检验结果，样本量小于50时用Shapiro-Wilk检验结果。

如表所示，显然腰围和体重两个变量都是服从正态分布的，所以可以采用Pearson相关系数。下面在计算相关系数时，将采用Pearson相关系数。

第3步：计算相关系数

在SPSS中，计算相关系数的操作步骤如下：

1. 打开数据文档，点击【分析 - 相关 - 双变量】，进入相关分析界面。

2. 将要判断的几个变量全部选入变量列表，确定，即可得到相关系数矩阵。确定后得到如下的相关系数矩阵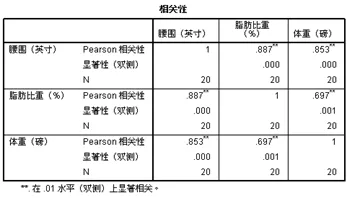：显然，相关系数矩阵是对称矩阵，而且对角线上的相关系数全为1（即变量自身的相关系数为1）。从上表中可知，腰围和体重的相关系数r=0.853，存在强相关；脂肪比重和体重的相关系数r=0.697，存在中度相关。

第4步：显著性检验

在SPSS中，不但计算出变量间的相关系数，同时还进行了显著性检验（即计算了统计量t，且查询出对应的概率P值，见显著性一行）。

在相关系数矩阵中，查看显著性一行，腰围和体重对应的概率P=0.000（因精度的原因，看起来概率为0），显然P<0.05，即根据显著性检验，也可知腰围和体重、脂肪比重和体重，都存在显著的线性相关关系。

第5步：进行业务判断

根据前面的相关分析，可得到数据分析结论：

1. 根据显著性判断，可知腰围与体重、脂肪比重与体重，都存在显著线性相关性。

2. 根据相关系数，可知腰围与体重存在强相关，脂肪比重与体重存在中度相关。

然后，再从业务上对分析结果进行解读，并给出相应的业务策略或建议：

1. 业务解读：腰围对体重的影响很大，脂肪比重对体重的影响较大。

2. 业务建议：要减轻体重，最好先减小腰围，少吃脂肪类食物。

这样，就实现了从数据到业务的完整的相关分析过程。

Part5其他相关分析方法

常用的三种相关性检验技术，Pearson相关性的精确度最高，但对原始数据的要求最高。Spearman等级相关和Kendall一致性相关的使用范围更广，但精确度较差。

下面介绍Spearman等级相关和Kendall一致性相关方法，并用实际案例说明如何用SPSS使用这三种相关性分析技术。

Spearman相关

当定距数据不满足正态分布，不能使用皮尔逊相关分析，这时，可以在相关分析中引入秩分，借助秩分实现相关性检验，即先分别计算两个序列的秩分，然后以秩分值代替原始数据，代入到皮尔逊相关系数公式中，得到斯皮尔曼相关系数公式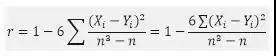：数据要求

• 不明分布类型的定距数据；

• 两个数据序列的数据一一对应，等间距等比例。数据序列通常来自对同一组样本的多次测量或不同视角的测量。

结论分析

在斯皮尔曼相关性分析中，也能够得到相关系数（r）和检验概率（Sig.），当检验概率小于0.05时，表示两列数据之间存在相关性。

Kendall相关

当既不满足正态分布，也不是等间距的定距数据，而是不明分布的定序数据时，不能使用Pearson相关和Spearman相关。此时，在相关分析中引入“一致对”的概念，借助“一致对”在“总对数”中的比例分析其相关性水平。Kendall相关系数计算公式如下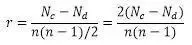：Kendall相关实质上是基于查看序列中有多少个顺序一致的对子的这个思路来判断数据的相关性水平。在Kendall相关性检验中，其核心思想是检验两个序列的秩分是否一致增减。因此，统计两序列中的“一致对”和“非一致对”的数量就非常重要。下面举例说明Kendall相关系数的计算过程：

假设有两个数据序列A和B的秩分序列分别是{2,4,3,5,1}，{3,4,1,5,2}，即相对应的秩对为(2,3)(4,4)(3,1)(5,5)(1,2)。在按照A的秩分排序后，得到新的秩对(1,2)(2,3)(3,1)(4,4)(5,5)，此时B的秩分序列变成了{2,3,1,4,5}。在这种情况下，针对第一个B值2，后面有3,4,5比它大，有1比它小，所以一致对为3，非一致对为1；第二个数字3，有4,5比它大，有1比它小，所以一致对为2，非一致对为1；依次类推，总共有8个一致对，2个非一致对。即Nc=8，Nd=2。

数据要求

适用于不明分布的定序数据；

Pearson相关适用于正态分布定距数据；Spearman相关适用于不明分布定距数据；Kendall相关适用于不明分布定序数据。

结论分析

在肯德尔相关性分析中，能够得到两个数值：相关系数（r）和检验概率（Sig.），当检验概率小于0.05时，表示两列数据之间存在相关性。

案例分析

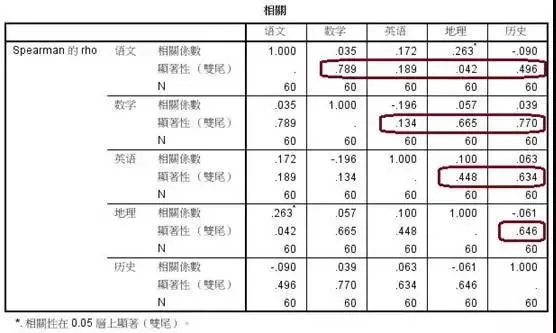
现在有一份《学生成绩数据》，如下图所示。请分析其中的语文、数学、英语、历史、地理成绩之间的相关性: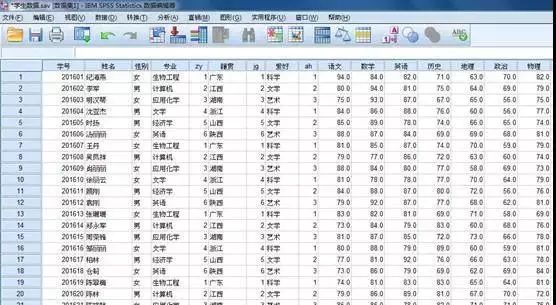解题思路

观察图中数据可知，需要分析的数据都是定距数据，而且它们来自同一组样本（同一批学生）的多次多视角测试（不同学科考试），可以使用Pearson相关分析和Spearman相关分析。先对原始数据进行正态分布检验，对于满足正态分布检验的变量使用Pearson相关性分析，不满足正态分布检验的变量则使用Spearman等级相关检验。

解题步骤

1. 利用【分析】-【非参数检验】-【旧对话框】-【1样本K-S】命令对语文、数学、英语、历史和地理成绩进行正态分布检验。

2. 利用【分析】-【相关】-【双变量】命令，在相关系数中选择【Pearson】，对语文、数学、英语和地理成绩进行Pearson相关性检验。

3. 利用【分析】-【相关】-【双变量】命令，在相关系数中选择【Spearman】，对历史、语文、数学、英语和地理成绩进行Spearman相关性检验。

结果解读

1. 正态性检验结果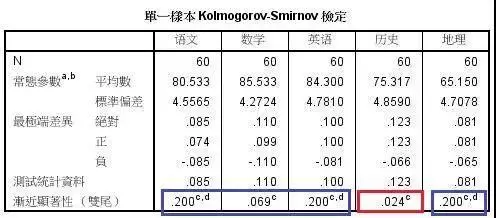；发现除历史以外，其它数据变量的检验概率都大于0.05，都符合正态分布。

2. 在皮尔逊相关分析中，语文、数学、英语和地理成绩之间的所有检验概率都大于0.05，说明它们之间都不存在相关性；同时，皮尔逊相关系数都小于0.4，也证明了它们之间没有相关性。

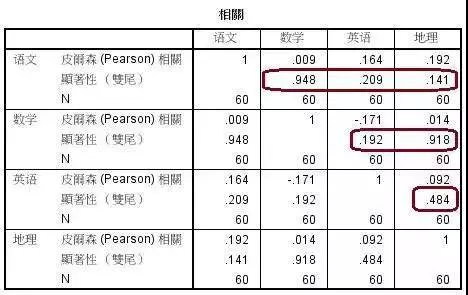
3. 在斯皮尔曼相关分析中，历史、语文、数学、英语和地理之间的检验概率除了地理和语文之间小于0.05以外，其它都大于0.05。但这不能说明地理与语文成绩之间存在相关性。观察它们的相关系数为0.263，这说明它们之间也不存在相关性。在确定变量之间相关性时，应该结合检验概率与相关系数进行分析。不能只看其中一个数值就确定变量之间的相关性。

Part6延伸思考：相关分析可能不靠谱

大家在电视上随处可见的广告或者新闻标题的句式：“想要A吗？那就来用B吧！”或者“研究表明，C物质会降低得D疾病的风险”， 又或者“E为你摆脱F的烦恼！”特别熟悉吧，是不是直接就被洗脑了？如果没有做过谨慎全面的实验设计和统计分析，就草率地下这种因果关系的结论啊，很可能造成坑爹坑妈坑群众的后果。市面上关于因果关系的论断，很多时候是表象上的相关分析而已。

例一：想长寿吗？来吸烟吧！（……）

这个例子是一个基于合理数据的严肃研究。英国某健康研究机构随机抽取出了1314名志愿者，其中582名吸烟者，732名不吸烟者。20年后，跟踪调查显示，吸烟者的死亡率24%，而不吸烟者死亡率为31%，并给出了这样一份统计报告（部分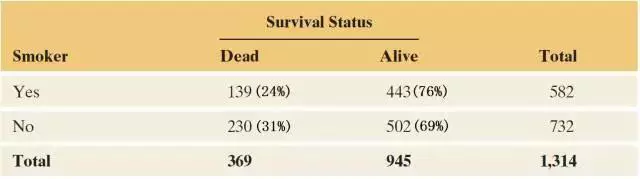）：有表有真相，吸烟者的死亡率比不吸烟者还要低。这1314名是随机抽取出来的，能够代表全民。问题不在数据，那就是分析的问题了，一定是我们漏掉了什么重要的东西。

那我们再来回头看看还能从数据中找出来点儿什么。可能有朋友已经想到了，数据有缺失信息（比缺失值更甚），没错，年龄。在这随机抽取的1314个人里面，我们统计了一下，吸烟者中65岁以上的老年人只占8.4%，而不吸烟者中的老年人却占到了26.4%。这种年龄不均衡性就可以解释上述的现象了：不吸烟组他们的死亡率高是没错，但可不是因为人家不吸烟啊，而是因为本来这组老年人的比例就高，那20年以后自然死亡或者是患某种致命的疾病的几率本来就大啊！

那么发现了这个现象之后我们应该怎么办呢？有统计经验的朋友可能已经知道了，分组。那我们就再按年龄分组来做一次列联表，看看每一个年龄组的死亡率在吸烟者和不吸烟者中有什么差别。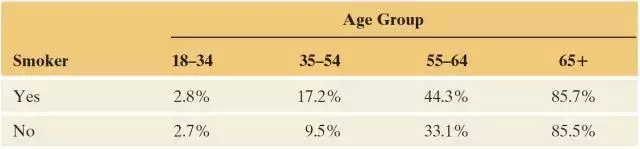可以看到，在34岁以下的青年人中，吸不吸烟影响不大，因为20年后的死亡率都很低，而在65岁以上的老年人中，其实吸不吸烟影响也不大，因为过了20年之后，他们都85岁以上了，死亡率本来就很高。但对于35岁到64岁之间的人群，不吸烟组比吸烟组的死亡率低了那可不是一点两点。如果看表格会把你搞晕的话，来看一下下面一目了然的分组柱状图。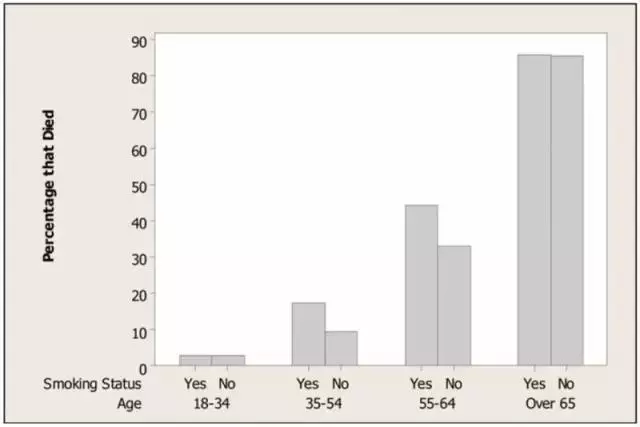看到这儿呢，你可以长吁一口气了，如果只是看否吸烟和死亡率，它们真的会出现这种“越吸烟越长寿”的奇怪的现象。但这只是表象上的关联性，或者说相关性，我们不能盲目地把它描述为因果关系。“吸烟组的死亡率比较低”这种说法指的是相关性，只是我们观察到的一种表象，它并不等价于“因为吸烟，所以死亡率低”或者“吸烟会导致死亡率降低”这种带有逻辑性推理的因果关系。

这个例子是因为我们之前忽略了一个可能很重要的变量“年龄”，这种会对结果产生重大影响但是却没有被考虑在列的变量，我们把它叫做“潜在变量”（lurking variable）。它有时候真可谓是“杀人于无形之中”，稍不注意就可能会要了整个统计分析报告的命。这种结果直接被潜在变量给反转的现象，我们在统计学里面称之为辛普森悖论（Simpson’s Paradox）。

例二：犯罪率和教育

如果说今天报纸的头条是这样写的：“美国高等教育现状令人堪忧：高学历更易引发犯罪”，你会有什么反应？是不是迫切地想知道为什么会造成这样的社会现象：是读书读多了压力过大容易变态吗？还是高学历社会认同感不够导致了容易仇视社会？还是美国高等教育真的有问题？然后又联想到几例最近听到的美国高校枪杀案呢，还有各种高科技犯罪的新闻，马上把这篇报道转到票圈，呼吁亲朋好友不要再到美国去留学了。

看完此篇文章以后，下次在思考这些问题之前，可以先对这种言论本身持一种怀疑态度，关心一下这个研究究竟是怎么做的？数据是哪儿来的？而分析又是怎么进行的？

这份数据是从美国各地区人群普查得到的，包含当地犯罪率以及用来代表教育水平的高中以上学历的居民比例。由于这两个变量都是连续变化的，之前那种针对分类数据的列联表就不能用了，我们需要在统计分析中每天都要用的散点图（scatter plot）来找一下灵感。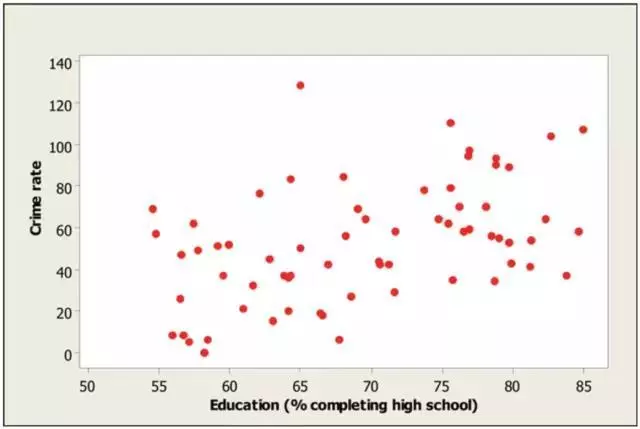从这个散点图中，我们确实能看到，随着教育水平的增高，犯罪率真的有些许上升的趋势。而且二者之间的皮尔森相关系数（Pearson correlation）是0.47，正相关关系。到这儿我们是不是可以把这个结果交由心理学家或者社会学家或者教育家去研究，统计分析是不是就结束了呢？其实，我们能做的远不止这点。根据上一个吸烟使人长寿的例子，思考一下，这种表象上的相关性会不会跟某个潜在变量有关呢？

人口普查其实还会得到很多有用的数据，根据常识，我们可以初步确定几个候选的潜在变量。在这里我们就来讨论一个最有可能的潜在变量：城市化程度。也就是说，每个地区在大城市生活的居民比例。如果我们把所有数据根据城市化程度划分成三组，我们就会得到如下的分组散点图。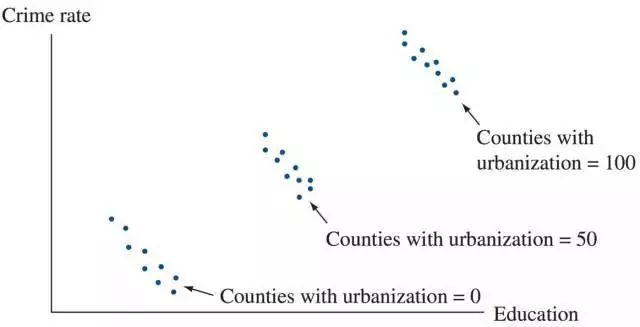在类似的城市化程度上，教育水平是跟犯罪率是负相关的！而随着城市化程度越来越高，其实犯罪率和教育水平都会升高，这一点是跟我们的常识相符的。美国的大城市犯罪率就是要高一些，而大城市的居民通常更有可能接受到高中以上的教育。所以之前我们看到的教育水平和犯罪率的正相关性其实并没有太大的参考价值。标题党的说法也就不攻自破了。

以上两个例子都属于辛普森悖论的范畴。有些看似的新发现啊、新言论啊，其实只是因为少考虑了一些潜在变量。

这类问题的常见种类总结如下：

第一种，本来是负相关的，因为被潜在变量影响而变成了正相关。这就是上述所说的辛普森悖论。

第二种，本来不相关的，是完全由于潜在变量导致的相关性。

举个例子，澳大利亚黄金海岸因为有很多美丽的沙滩而世界闻名。但不幸的是，每年都会有人在那里溺水身亡。现在如果你做一下黄金海岸溺水身亡的人数和当地冰激凌销售业绩的分析，它们会有很强的正相关性。因为冰激凌的销售量变大导致溺水人数变多吗？或者说如果想让溺水的人少一些，是不是号召大家少买点冰激凌就好了呢？

正常人都知道这种正相关性是因为炎热天气下冰激凌更受欢迎，同时更多人会去游泳而导致溺水的人可能变多。这本身是一个非常明显的例子，所以大家不觉得自己会拎不清，但如果一个健康广告说“最新研究结果显示，优质胆固醇会降低心血管疾病的发病风险”，然后顺带推销几种优质胆固醇的保养品，你会不会头脑一热就去给你的长辈买了？

第三种，表象上的相关性有的时候呢，是由于时间趋势和先后造成的。

本科毕业答辩的时候可以见到太多的例子，就是这种原因造成的盲目的因果关系的推断。比如说我们收集了近20年来中国的离婚率和犯罪率的数据，发现离婚率越高犯罪率越高。那么可以直接推出离婚的人更容易有犯罪倾向吗？当然不。因为这种现象，主要是由于二者都是时间序列（time series）这种数据，那离婚率和犯罪率都会随着时间推移而逐渐上升，也就是说离婚率越高，说明数据的时间节点越晚，而对应的犯罪率就会越高。还有个经典的例子就是，公鸡打鸣后，太阳从地平线升起，这两者之间有关系，但一定不会是因果关系。

又比如啊，如果你做一下房价和手机使用率的相关关系，那在过去的这二十几年里面，它们肯定也是正相关。那大家为了能买得起房子是不是少用点儿手机就可以了呢？这都是显而易见的对吧？

第四种，即使普遍认为是有相关关系，但是没法证明内在机制，或者不确定谁是因谁是果。

上面的吸烟使人长寿的例子大家都知道是在忽悠，那么“吸烟可能导致肺癌”却是一个被普遍认可的观点。但是其实呢，从20世纪初直到现在，这种因果关系都受到科学界的各种质疑或者说怀疑。比如说也许肺癌与吸烟习惯的背后有一种共同的遗传因素只是人们还没有找到？现代统计学之父R.A. Fisher大家都认识吧？至少可能学统计的同学会认识他。他当时甚至认为，不排除“由肺癌导致吸烟”的这样一种可能性——也许在即将患上肺癌时，人们开始感觉不舒服或者感到烦躁，这时候比平常更容易吸上一支香烟来应对。这种论调呢，现在看来可能有点荒唐，但是的确给我们打开了一扇不走寻常路的这种逻辑门，避免我们落入定式思维的圈套。

论证因果关系是件挺难的事，单纯从表面的相关关系是不能直接推出因果关系的，而我们日常生活或者科学研究领域经常会犯这种错误。有很多方法可以去验证因果关系的存在，比如说我们可以进行实验性研究（experimental study），或者针对观察性研究（observational study）采用倾向得分匹配（propensity score matching）之类的统计技巧。

还有的朋友说，大数据时代，我们最在乎预测未来，比如说预测股票走势、预测地震台风、预测城市发展前景等等等等。其实可以不去理会那么复杂的因果关系，只要知道相关关系就足够了。没错，“预测”（prediction）是数据分析的主要目的之一。你如果知道下一个月的冰淇淋销售量，确实可以差不多预测出溺水死亡的人数。或者反过来，你知道某个时期溺水死亡的人比较多，也可以估计出这个时期应该冰淇淋销售业绩也不会太差。在预测的层面上，你并不用管是不是冰激凌的销售情况直接导致溺水死亡人数的变化。

但更多的时候呢，我们是需要知道事物之间的内在机制的，特别是在科学研究领域。比如在提出类似“优质胆固醇会降低心血管疾病的发病风险”这种言论的时候啊，只研究优质胆固醇和心血管疾病的相关关系显然是不够的。你必须保证增加此胆固醇的摄入真的会直接导致心血管疾病发病风险降低，而不是其他的什么假象。

数据分析和最终面向大众的言论中间有一道被忽略了的鸿沟，这道鸿沟的一边是“表面上的相关关系”，另一边是“机理上的因果关系”，而我们经常把这道鸿沟不自觉地就模糊掉了。有的时候这种因果关系并不重要，比如你只关心预测，那你就把言结论止于相关关系就万事大吉了，千万别多说多错。还有的时候，因果关系它本身是重要的，那就需要我们用更加仔细更加严谨的统计思维和方法去进一步探讨因果关系的存在性。如果从相关关系这个时候你直接一个大跨步，即使你有两米的大长腿，也逃不了掉到沟里的命运。

本文内容参考了以下文章：

1. 相关分析：从概念到步骤. 微信公众号：量化研究方法. 20190224

2. 相关分析表明：相关分析不靠谱！.媛子老师. 微信公众号：狗熊会.  20160725

3. SPSS分析技术：Pearson相关、Spearman相关及Kendall相关. 东山草堂. 微信公众号：生活统计学. 2016101