一起刷 leetcode 之旋转矩阵(头条/华为/陌陌真题)
微信公众号:[每天晒白牙]
关注可了解更多的编程知识。问题或建议,请公众号留言;
如果你觉文章对你有帮助,欢迎关注与
题目描述
给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?
https://leetcode-cn.com/problems/rotate-matrix-lcci/
示例
示例 1
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]示例 2
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]分析
方法 1:借助额外数组存放旋转后的元素
按行旋转,找旋转前和旋转后元素的坐标对应关系
原始矩阵
1 2 3
4 5 6
7 8 9
把第一行顺时针旋转 90 度后为:
x x 1
x x 2
x x 3
对应的坐标关系如下所示:
1:(0,0) -> (0,2)
2:(0,1) -> (1,2)
3:(0,2) -> (2,2)
把第二行顺时针旋转 90 度后为:
x 4 1
x 5 2
x 6 3
对应的坐标关系如下所示:
4:(1,0) -> (0,1)
5:(1,1) -> (1,1)
6:(1,2) -> (2,1)
第三行也类似,就不一一列出了,通过旋转前和旋转后坐标的对比,我们可以得出一个很重要的规律
旋转前元素的坐标:(row,col)
旋转后元素的坐标:(col,n-row-1)
matrix[row] [col] = matrix[col] [n-row-1]
这个规律很重要,下面方法也会用到
方法就很简单了,我们遍历矩阵,根据上面得出的旋转前后的对应关系,把元素放到新的位置上,这里我们用额外矩阵来存放旋转后的元素,然后在最后把新矩阵复制到之前的矩阵中
源码
public static void rotate(int[][] matrix) {
int n = matrix.length;
if (n == 0) {
return;
}
// 新建一个矩阵用来存放旋转后的元素
int[][] newMatrix = new int[n][matrix[0].length];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
// 根据旋转前后的对应关系把元素放到要旋转的位置上
newMatrix[j][n - i - 1] = matrix[i][j];
}
}
// 把存放旋转后元素的矩阵复制到原先的矩阵上
System.arraycopy(newMatrix, 0, matrix, 0, newMatrix.length);
}执行结果
复杂度分析
时间复杂度:O(n^2)
空间复杂度:O(n^2)
方法 1 占用了额外的内存空间,其实这道题是可以不额外占用空间也能实现,我们一起来看下下面的方法吧
方法 2:原地进行旋转操作
如果不借助额外数组该怎么操作?
在方法 1 中我们找到了规律是元素 matrix[row] [col] 旋转到了 matrix[col] [n-row-1] ,如果不借助额外数组,matrix[col] [n-row-1] 就会被覆盖,所以需要先把 matrix[col] [n-row-1] 临时存起来,下面就一起分析下不借助额外数组进行原地旋转吧,分析过程比较枯燥,建议自己尝试一下,省的跟丢
先把 matrix[col] [n-row-1] 存放到 temp 上,然后把 matrix[row] [col] 旋转到 matrix[col] [n-row-1]
temp = matrix[col] [n-row-1]
matrix[col] [n-row-1] = matrix[row] [col]
那 matrix[col] [n-row-1] 要旋转到什么位置上呢?这里需要方法 1 得出的重要规律
matrix[row] [col] = matrix[col] [n-row-1]
这里需要注意的是新的 row = col;col = n-row-1,将其代入上面的规律中后为
matrix[n - row -1] [n - col -1] = matrix[col] [n - row -1]
可知,matrix[col] [n - row -1] 旋转后的位置是 matrix[n - row -1] [n - col -1],这个位置也会被覆盖,所以还需要用 temp 做中转
temp = matrix[n - row -1] [n - col -1]
matrix[n - row- 1] [n - col-1] = matrix[col] [n - row -1]
matrix[col] [n-row-1] = matrix[row] [col]
我们继续往下推导,matrix[n - row -1] [n - col -1] 要旋转到什么位置上?依然代入方法 1 的重要规律中
matrix[row] [col] = matrix[col] [n-row-1]
这里需要注意的是新的 row = n - row -1;col = n - col -1,将其代入上面的规律中后为
matrix[n - col - 1] [row] = matrix[col] [n - row -1]
可知,matrix[n - row -1] [n - col -1] 旋转后的位置为 matrix[n - col - 1] [row] ,但这个位置也会被覆盖,依然需要用 temp 做中转
temp = matrix[n - col - 1] [row]
matrix[n - col - 1] [row] = matrix[n - row -1] [n - col -1]
matrix[n - row -1] [n - col -1] = matrix[col] [n - row -1]
matrix[col] [n - row -1] = matrix[row] [col]
不要放弃,继续推导,matrix[n - col - 1] [row] 旋转到设么位置上?代入方法 1 的重要规律中
matrix[row] [col] = matrix[col] [n-row-1]
这里需要注意的是新的 row = n - col - 1;col =row ,将其代入上面的规律中后为
matrix[row] [col] = matrix[n - col - 1] [row]
这次竟然发现了新大陆,matrix[col] [n - row -1] 旋转后的位置为 matrix[row] [col],最后又回到了起点
此刻脑子里飘来了《那些年,我们一起追过的女孩》中的歌词“又回到最初的起点,呆呆的站在镜子前……”
综合上面的推导,我们发现旋转的重点就是下面的 4 个元素是处于一个循环中的
matrix[row] [col]
matrix[col] [n - row -1]
matrix[n - row - 1] [n - col - 1]
matrix[n - col - 1] [row]
对于上面 4 个元素的交换,我们用一个 temp 就可以实现了。但还有一点需要我们思考,就是要枚举哪些位置的元素来进行原地交换,能保证不重不漏呢?因为一次原地交换需要 4 个元素参加。我们把 n 分为偶数和奇数来看
当 n 为偶数时,需要枚举 (n/2)*(n/2) = n^2/4 个位置,所以矩阵左上角的子矩阵就符合我们的要求,可以做到不重不漏
下面用 n = 4 来举个栗子,* 代表要枚举的位置
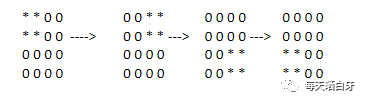
当 n 为奇数时,矩阵的中心位置是不动的,只需要枚举 ((n-1)/2)*((n+1)/2) = (n^2 -1/4) 个位置,矩阵的左上角的子矩阵还是符合要求的,可以做到不重不漏
下面以 n = 5 来举个栗子,* 代表要枚举的位置,x 代表中心位置
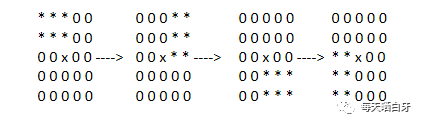
综上,我们只需要枚举矩阵左上角高为 n/2,宽为 (n+1)/2 的小矩阵就好了,就可以做到不重不漏
源码
public static void rotate2(int[][] matrix) {
int n = matrix.length;
if (n == 0) {
return;
}
for (int row = 0; row < n / 2; row++) {
for (int col = 0; col < (n + 1) / 2; col++) {
// 把 4 个位置的元素互换,注意顺序
int temp = matrix[n - col -1][row];
matrix[n - col -1][row] = matrix[n - row -1][n - col -1];
matrix[n - row -1][n - col -1] = matrix[col][n-row-1];
matrix[col][n-row-1] = matrix[row][col];
matrix[row][col] = temp;
}
}
}
执行结果

复杂度分析
时间复杂度:O(n^2)
空间复杂度:O(1),这个方法没有额外使用空间
方法 2 的难点是找到 4 个元素位置的坐标关系,然后找到可以枚举的不重不漏的子矩阵,方法已经很优秀了,但是广大技术友总是能找到更牛逼的方法,下面的方法是从数学的角度来做到矩阵的原地旋转
方法 3 :原地双百
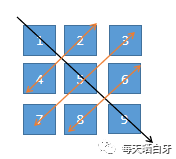
主要思想是用翻转代替旋转,先以对角线为轴,进行翻转。再以每一行的中点为轴,进行翻转。
我们通过示例图来看下这个过程
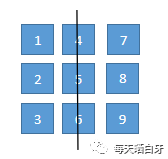
对于原始矩阵,先以对角线为轴,进行翻转
翻转完后如下所示:
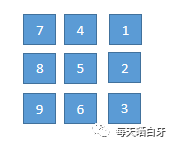
然后对每一行以中点为轴,进行翻转,效果如下:
以对角线进行翻转时,我们只需要枚举对角线上方的元素,然后和下方元素进行交换,坐标对应关系如下
matrix[row] [col] --> matrix[col] [row]
对每行以中点进行翻转时,我们只需要枚举中点左边的元素,然后和右边的元素进行交换,坐标对应关系如下
matrix[row] [col] --> matrix[row] [n - col - 1]
源码
public static void rotate3(int[][] matrix) {
int n = matrix.length;
if (n == 0) {
return;
}
// 以对角线进行翻转
for (int row = 0; row < n; row++) {
for (int col = row + 1; col < n; col++) {
int temp = matrix[col][row];
matrix[col][row] = matrix[row][col];
matrix[row][col] = temp;
}
}
// 对每一行以中点进行翻转
for (int row = 0; row < n; row++) {
for (int col = 0; col < n / 2; col++) {
int temp = matrix[row][n - col - 1];
matrix[row][n - col - 1] = matrix[row][col];
matrix[row][col] = temp;
}
}
}
执行结果
这种方法很巧妙,一般很难想到,所以只要你多刷肯定能学到一些比较好的方法,这种方法就是你看到过,你就会,没看到过,可能就需要好好想想了,最终还不一定能想到
但这个方法还可以优化,可以把按对角线翻转按中点翻转放到一个大 for 循环下
源码
public static void rotate4(int[][] matrix) {
int n = matrix.length;
if (n == 0) {
return;
}
for (int row = 0; row < n; row++) {
// 以对角线进行翻转
for (int col = row + 1; col < n; col++) {
int temp = matrix[col][row];
matrix[col][row] = matrix[row][col];
matrix[row][col] = temp;
}
// 对每一行以中点进行翻转
for (int col = 0; col < n / 2; col++) {
int temp = matrix[row][n - col - 1];
matrix[row][n - col - 1] = matrix[row][col];
matrix[row][col] = temp;
}
}
}
执行结果

复杂度分析
时间复杂度:O(n^2)
空间复杂度:O(1) 没有使用额外的空间
用过该题做过面试题的公司

其实有技术友分享过陌陌公司去年使用过这道题作为笔试题,不知道今年还有没有,遇到的小伙伴可以留言说下

陌陌真题-技术友分享
推荐阅读
老年代又占用100%了,顺便发现了vertx-redis-client 的bug
三面阿里被挂,幸获内推名额,历经 5 面终获口碑 offer
