样例
示例 1:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,3,6,9,8,7,4,5]
示例 2:
输入:
[
[1, 2, 3, 4],
[5, 6, 7, 8],
[9,10,11,12]
]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]
解题
https://www.cnblogs.com/techflow/p/12790451.html通过螺旋丸我们都知道螺旋形是什么意思，所以所谓的螺旋矩阵，就是按照螺旋形的顺序来遍历一个数组，或者说矩阵。我们可以看下下图：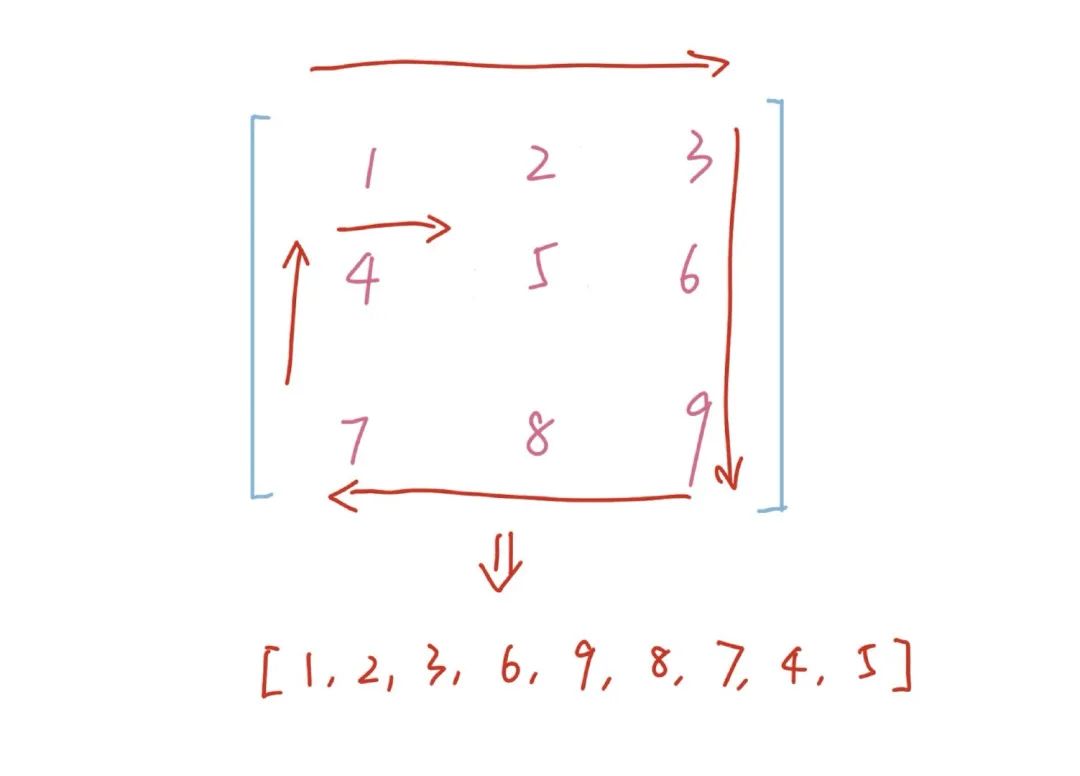
箭头标注的顺序就是螺旋的顺序，这道题让我们求的就是按照螺旋的顺序遍历之后的结果。背景
这道题的题意非常简单，我想大家肯定都能看明白，但是真的要上手去做会发现还是蛮困难的。主要的难点就是我们遍历的顺序一直在变化，并且变化的速度也是在变化的。虽然从某种程度上来说，这些变化都是有迹可循的，但是即便如此，把这些规律抽象出来写成简单易懂没有bug的代码也并不是一件容易的事情。如果我没有记错的话，当年我大二的时候学校里的acm校赛有一题就是这个，一模一样的原题。虽然非常简单，每个人都知道怎么做，但是最后的通过率并不高。这并不完全是出题人的恶意，其实这类问题在acm的比赛当中还是很常见的。经常会有一些题目很清晰明确，你只需要照着实现就可以了的题目。考察的就是选手的抽象和编码能力，虽然题意不难，但是在比赛高压的场景下想要快速写出一个几百行包含一系列复杂逻辑的程序并且没有bug，还是非常困难的一件事。由于这类题目的关键就是让我们模拟出来题目的意思，所以也被称为模拟题。想要比较顺手地写出这道题，需要一个很常用的技巧或者说惯例，这也是这篇文章的关键。方向数组
在许多问题当中我们经常会遇到这样一个问题，比如我们需要遍历一个迷宫，需要沿着现实世界当中上下左右或者是东南西北的方向进行移动。在移动的过程当中自然就涉及各种各样的方向，于是我们需要用代码来表示方向。比如我们画一个小人，它所在的坐标是(x, y)，它有东南西北四个方向可以选。我们假设他每次移动一个单位的距离，我们很容易就得出它往各个方向移动之后的新坐标。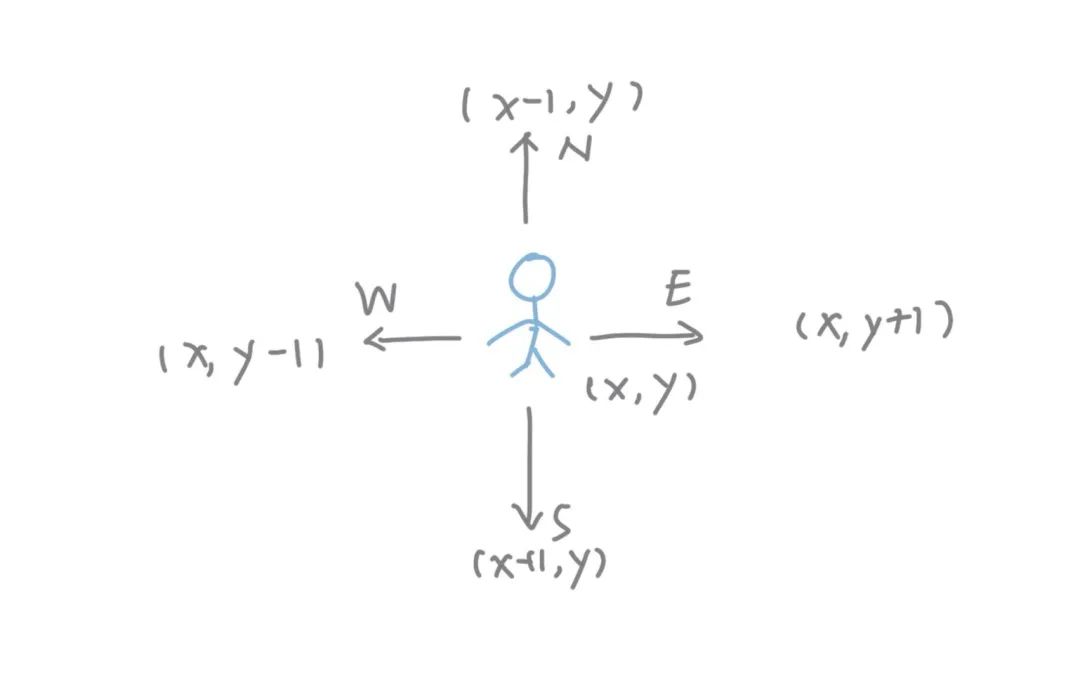
根据数学上向量的定义，我们可以写出这四个方向的方向单位向量：[0, 1], [0, -1], [1, 0], [-1, 0]。我们把这些向量存放进一个常量数组当中，就得到了方向数组。当我们需要遍历所有方向的时候，我们只需要遍历这个数组即可。不仅如此，如果我们对方向的遍历顺序有要求，它也完全可以实现。比如在这题当中，我们可以发现，螺旋遍历每一次改变顺序其实都是向左转了90度。原本朝东的旋转之后变成了朝南，朝南的变成了朝西，朝西的成了朝北，而朝北的成了朝东。那么我们只需要把方向按照东南西北的顺序摆放，我们每次把方向数组的下标增加一位并对4取模，就得到了下一个方向。解答
理解了方向数组之后剩下的就容易多了，我们观察一下上面螺旋遍历的过程，每一次改变方向遍历的长度虽然不同，但是每一次改变的原因是一致的，就是这个方向上已经遍历到头了，所以我们需要变更方向。明白了这点其实就很容易了，我们只需要维护每个方向上的终点，每次到终点则进行变向。由于矩阵当中元素的数量是固定的，我们遍历的次数也就知道了，所以只要把变更方向的事情处理好，这道题也就解决了。class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
# 定义方向数组
fx = [[0, 1], [1, 0], [0, -1], [-1, 0]]
n = len(matrix)
if n == 0:
return []
m = len(matrix[0])
ret = []
# 定义边界数组
# 边界数组和旋转的顺序也是对应的
# 第一次旋转之后上边界+1，所以第0位是上边界
# 第二次旋转之后，右边界-1
# 以此类推
condition = [0, m-1, n-1, 0]
x, y, dt = 0, 0, 0
for i in range(n * m):
ret.append(matrix[x][y])
x_, y_ = x + fx[dt][0], y + fx[dt][1]
# 如果已经越过边界了，则需要转向
if x_ < condition[0] or x_ > condition[2] or y_ < condition[3] or y_ > condition[1]:
# 更新边界
if dt in (1, 2):
condition[dt] -= 1
else:
condition[dt] += 1
# 转向，并且重新移动
dt = (dt + 1) % 4
x_, y_ = x+fx[dt][0], y+fx[dt][1]
# print(x_, y_)
x, y = x_, y_
return ret
我们观察一下代码，还有一个我们刚才没有提到的细节。我们在移动的时候，并不是直接在原变量上进行变更，因为如果一旦移动超界或者触发其他非法的情况，那么我们就无法回滚了。所以我们会创建新的x和y的变量来表示移动之后的位置，即使移动到了非法位置，也不会影响之前的结果。这也是一个常用的技巧，在Python当中，我们在变量末尾加上下划线表示这是一个影子（克隆）变量。总结
我个人认为今天的题目出得不错，初学者很有必要亲自动手做一下。因为在做题的过程当中我们可以很具体地学到方向数组这个很有用的解题技巧，它在搜索问题当中广泛使用，可以说是做算法题必须会的技巧之一。可能你会觉得我们通过边界判断是否需要转向的逻辑看起来有些复杂，这并不是必须的。我们也可以使用一些其他方法来代替，比如我们可以开辟一个数组记录已经遍历过的位置来代替边界的判定，和使用边界判定的方法相比，这样做消耗的空间要更大一些，并且通过边界判定的方法更加考验思维一些，因此我个人比较推荐。好了，今天的文章就到这里，如果觉得有所收获，请顺手点个在看或者转发吧，你们的支持是我最大的动力。
