LeetCode刷题实战48:旋转图像
算法的重要性,我就不多说了吧,想去大厂,就必须要经过基础知识和业务逻辑面试+算法面试。所以,为了提高大家的算法能力,这个公众号后续每天带大家做一道算法题,题目就从LeetCode上面选 !
今天和大家聊的问题叫做 旋转图像,我们先来看题面:
https://leetcode-cn.com/problems/rotate-image/
You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
题意
样例
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
我们来看两个动态图:

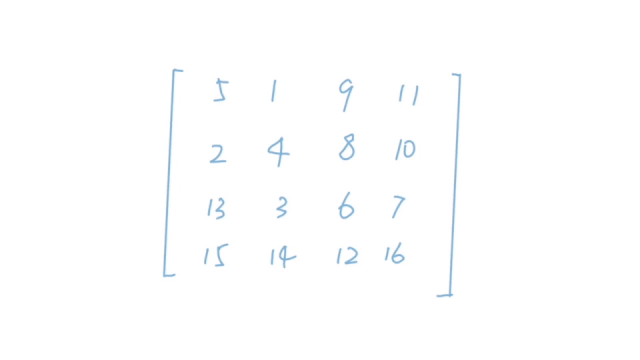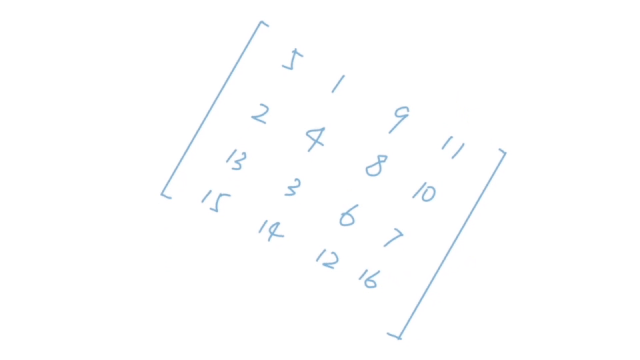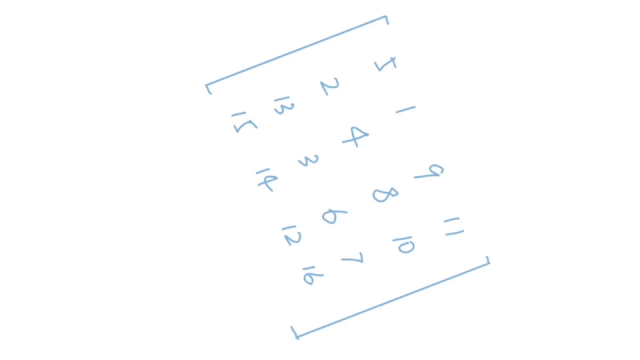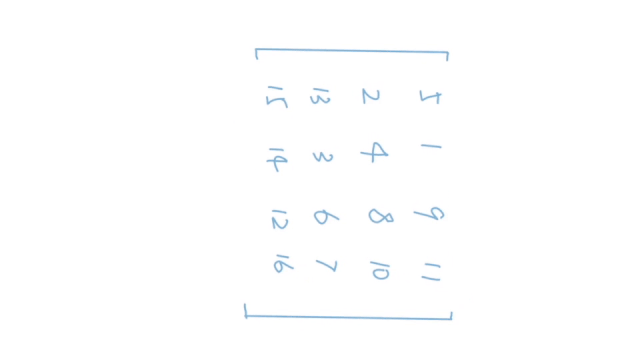
题解
https://www.cnblogs.com/techflow/p/12687271.html
这个动图一看就明白了,也就是说我们需要将一个二维矩阵顺时针旋转90度。这个题意我们都很好理解,但是题目当中还有一个限制条件:我们不能额外申请其他的数组来辅助,也就是对我们的空间利用进行了限制。
如果没有这个条件限制其实很容易,我们只需要算出每一个坐标旋转之后的位置,我们重新创建一个数组然后依次填充就行了。
我们忽略矩阵当中具体的数据,而来看看矩阵旋转前后的坐标变化。这是矩阵旋转之前的坐标:

旋转之后,坐标变成了:
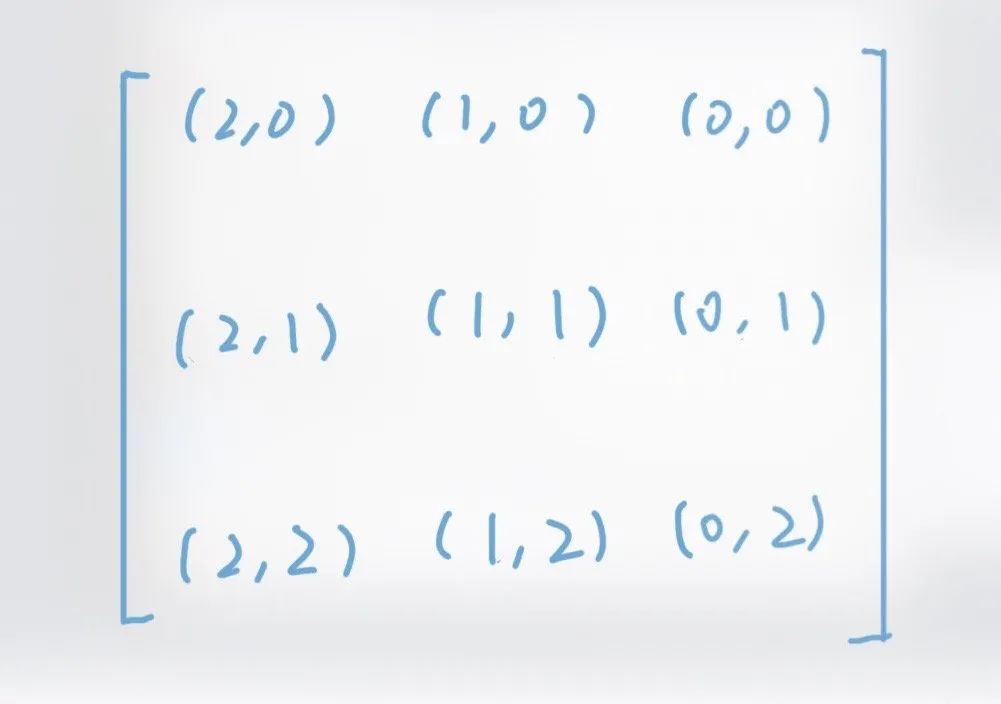
我们对照上面两张图观察一下,可以看出对于坐标(i, j)来说,它旋转90度之后得到的结果应该是(j, n-1-i)。这里的n是行数。
我们有了这个式子之后,我们可以继续推广。我们发现(i, j)位置的点旋转之后到了(j, n-1-i)。而(j, n-1-i)位置的点旋转之后到了(n-1-i, n-1-j),同理(n-1-i, n-1-j)旋转之后到了(n-1-j, i),最后我们发现(n-1-j, i)旋转之后回到了(i, j)。
也就是说对于一次旋转来说,(i, j), (j,n-1-i), (n-1-i, n-1-j), (n-1-j, i)这四个位置的元素互相交换了位置,并没有影响到其他位置。其实这个也是很容易想明白的,因为题目给定的是一个方阵。
我们看下下图就理解了:
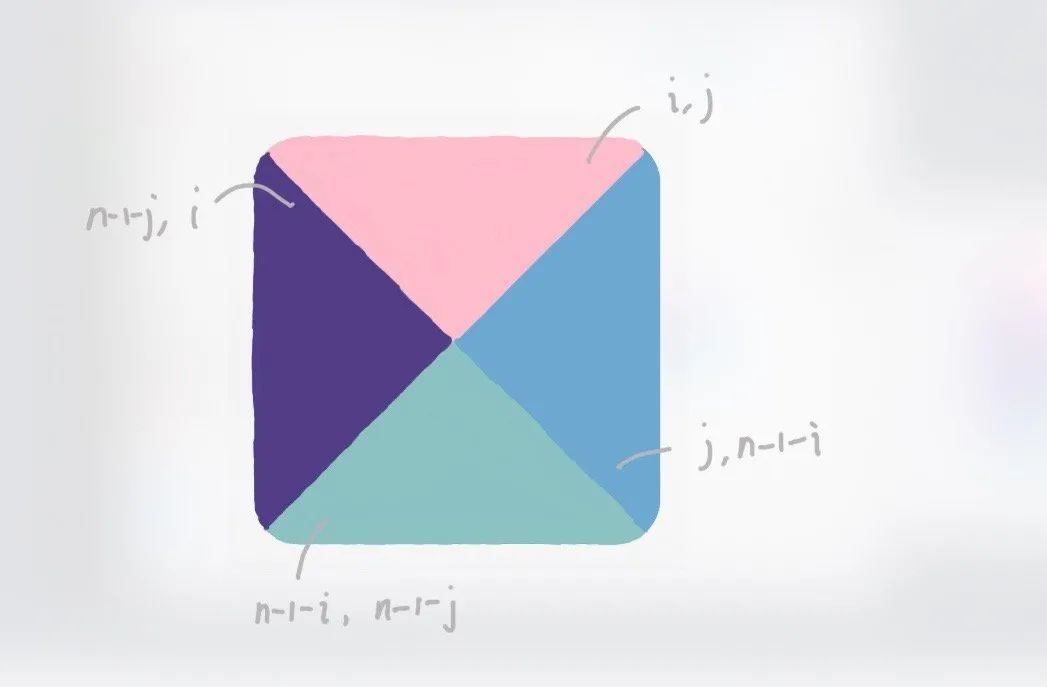
也就是说我们只需要遍历矩阵四分之一的部分,然后通过坐标拿到互相交换的4个位置,然后交换它们的元素即可。
代码
代码真的很简单,只有几行:
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
# 注意一下范围和下标即可
for i in range(n//2):
for j in range(i, n-1-i):
matrix[i][j], matrix[j][n-1-i], matrix[n-1-i][n-1-j], matrix[n-1-j][i] = \
matrix[n-1-j][i], matrix[i][j], matrix[j][n-1-i], matrix[n-1-i][n-1-j]上期推文:
