启示：分形、升维与第二曲线创新 | IDCF

一张A4纸有多长？

一张A4纸有多长？搜索的结果是：A4纸是由国际标准化组织的ISO 216定义的，规格为21*29.7cm（210mm×297mm）。

那么，如果揉成纸团呢？是应该直接测量直径，还是展开成平面进行测量？还能恢复原先的平整状态么？褶皱部分如何计量？

同样的问题存在于：英国的海岸线究竟有多长？

英国的海岸线究竟有多长？

上个世纪60年代，著名数学家芒德勃罗 Benoit B.Mandelbrot对困扰人们很多年的问题开始感兴趣：英国的海岸线究竟有多长？以此为题，1967年Mandelbrot在美国权威的《科学》杂志上发表了题为《英国的海岸线有多长？统计自相似和分数维度》（How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension）的著名论文，对这一问题深入探讨。

海岸线作为曲线，其特征是极不规则、极不光滑的，呈现极其蜿蜒复杂的变化。海岸线的长度，取决于你想要的精度。随着分辨率的提高，得到的长度会持续增长，随着放大倍数的增大，海岸线呈现出来的细节也就越多。

我们不能从形状和结构上区分这部分海岸与那部分海岸有什么本质的不同，这种几乎同样程度的不规则性和复杂性，说明海岸线在形貌上是自相似的，也就是局部形态和整体态的相似。在没有建筑物或其他东西作为参照物时，在空中拍摄的100公里长的海岸线与放大了的10公里长海岸线的两张照片，看上去会十分相似。

Mandelbrot把这些部分与整体以某种方式相似的形体称为分形(Fractal)。1975年，他创立了分形几何学(Fractal Geometry)。在此基础上，形成了研究分形性质及其应用的科学，称为分形理论。

理想化范式的欧几里得几何，与自然界的分形结构。

我们之所以测不准海岸线的长度，是因为海岸线就是一个天然的分形。

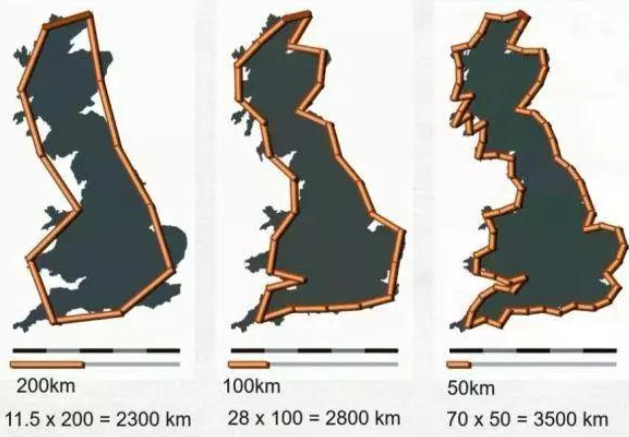
“平缓的形状在野外很少见到，但在象牙塔和工厂中极为重要”。

在这个人工制品的新世界，我们不可避免的习惯于通过蒙蔽我们的欧几里得几何（直线、平滑曲线和平滑表面）的滤镜观察世界，而我们所处的是一个混乱、复杂、不规则的令人费解的世界。

Mandelbrot认为别人视为不规则形状的东西恰恰是最普通的类型；别人视为想当然的无比美好的点、线、面、体却是例外。长期的观察、收集与总结，使Mandelbrot获得这样一个印象：除了光滑的欧氏几何（广义的，泛指分形几何以外的标准几何）以外，应该还有一种不光滑的几何，这种几何更适于描写大自然的本来面目。

根植于欧几里得几何的柏拉图式的平滑理想状态在我们灵魂深处根深蒂固，但是，自然界中，几乎没有什么东西是平缓的，大多数事物都是有褶皱的、不规则的、细圆锯齿的，通常都以一种自相似的形式存在。

在其代表著《大自然的分形几何学》中，Mandelbrot如是说：

“为什么几何学常常被说成是‘ 冷酷无情’和‘枯燥乏味’的?原因之一在于它无力描写云彩、山岭、海岸线或树木的形状。云彩不是球体，山岭不是锥体，海岸线不是圆周，树皮并不光滑，闪电更不是沿着直线传 播的。更为一般地，我要指出，自然界的许多图样是如此地不规则和支离破碎，以致与欧几里得(几何)──本书中用这个术语来称呼所有标准的几何学——相比，自然界不只具有较高程度的复杂性，而且拥有完全不同层次上的复杂度。自然界图样的长度，在不同标度下的数目，在所有实际情况下都是无限的。这些图样的存在，激励着我们去探索那些被欧几里得搁置在一边，被认为是‘无形状可言的’形状，去研究“无定形”的形态学。然而数学家蔑视这种挑战，他们想出种种与我们看得见或感觉到的任何东西都无关的理论，却回避从大自然提出的问题 。”

自然界的分形现象

在自然界令人畏惧的复杂性的背后，潜藏着惊人的简单性、规律性和一致性：褶皱，中断，粗糙和自相似性。

分形（Fractal）和物体的自相似性有很大联系。生活里面，我们发现许多自然生成的东西往往有极其复杂的细节，而且组成它们的微小部分就好像是整体的缩小版，它们在各个尺度上的复杂程度都很相似。蜿蜒的海岸线，发散的树枝，海螺的断面，这些都是自然生成的自相似图形。

具有自相似性的形态广泛存在于自然界中，如：连绵的山川、飘浮的云朵、岩石的断裂口、粒子的布朗运动、树冠、花菜、大脑皮层、血管网络、小溪、河流、山脉、闪电、股市K线。

启示一：创新第二曲线的分形创新

“一花一世界，一树一菩提”，说的是以小见大，从细微之处洞察宏观的哲学思考，而“一即是全，全即是一”，是对分形最传神的表达。

几乎所有维持生命的网络，都有自相似分形的特点。分析特点可以从个体扩展到公司、城市、州，甚至生命本身。

我们要熟悉充满抽象、褶皱、非欧几里得曲线和平面的奇怪世界，重拾被欧几里何经典几何的重复性、高度一致性所打压的自然创造力。

多样化，拥有更多可交替和适应性。自然选择因更强的多样性而发展，同样也创造出了更强的多样性，有韧性的生态系统也有更多样的物种。

创新也是如此，多样性对于创新而言至关重要。于此同时，S曲线告诉我们增长一定有拐点，无论大公司，还是小公司，要想突破第一曲线极限点，都必须通过创新，找到自己的第二曲线。

第二曲线不是凭空布局出来的，而是从第一曲线长出来的！

要有意识的梳理微创新，引入外部市场竞争机制，看是否能够生长成为第二条S曲线。

（以上内容来自于“IDCF黑客马拉松 - 第二曲线创新模块”）

注：IDCF DevOps黑客马拉松2021年赛事安排点击“阅读原文”或输入地址查看：https://j.mp/35bBHI2

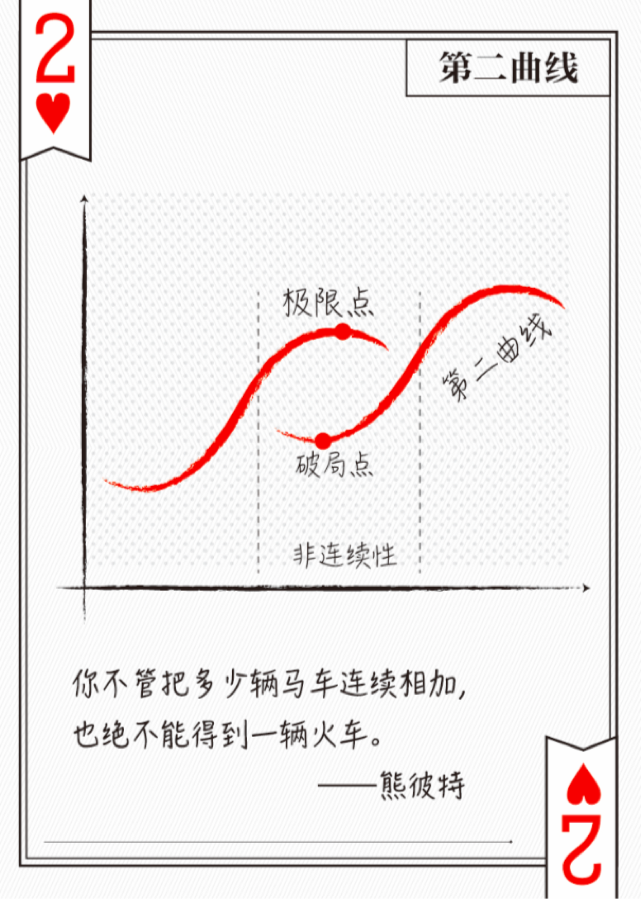
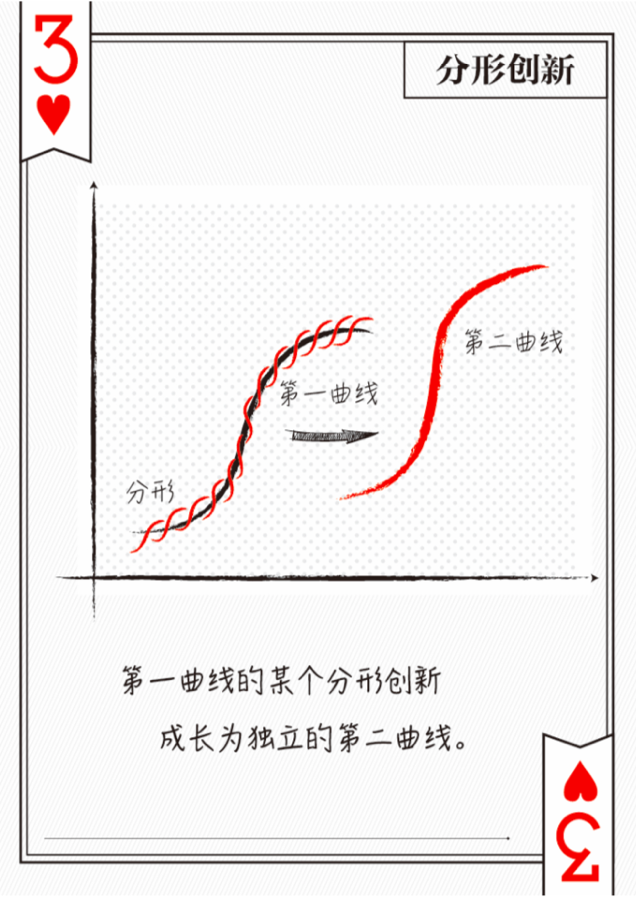
启示二：升维与降维

还记得A4纸与纸团么？A4纸是一个二维的物体（如果不考虑其厚度），而纸团则是三维空间的物体，A4纸到纸团的过程是升维的过程，升维产生了空间的折叠，而这些折叠体现在纸团的褶皱上。

Credit: evoluasuaconsciencia 时空概念

分维，又称分形维或分数维，作为分形的定量表征和基本参数，是分形理论的又一重要原则。长期以来人们习惯于将点定义为零维，直线为一维，平面为二维，空间为三维，爱因斯坦在相对论中引入时间维，就形成四维时空。

（分形维度更主要的是用来形容形体的不规则程度，和我们一般理解的时空的维度有所不同，详细区别可以查阅参考材料中的豆瓣链接）

纸团之所以能够在拳头大小的空间聚合了一整张A4纸的长度，是因为其升维。升维的力量在人体中的表现：

• 尽管你的肺只有一个足球那么大，但是血液中负责氧气和二氧化碳交换的肺泡的总表面就几乎有一个网球场那么大。
• 所有气流通路的总长度约为2500千米，这几乎是北京到深圳的距离。
• 如果把你循环系统中的所有动脉、静脉和毛细血管平铺开来，首尾连接，它们的总长度约为10万千米，差不多可以绕地球2.5圈！
• 所以一切整整齐齐的排列在人体中，令人难以置信，这也是自然选择的神奇之处！

在大刘的《三体》中，我们看到从0维的“世界即是一个无限小的点”到10维的囊括宇宙所有可能的“真理”世界，充分体验到了三维时空的你面对高维世界的无法想象与理解，以及随之而来的无力感。

几年前科幻作家郝景芳的中短篇小说《北京折叠》也描述了类似的场景，讲述北京在未来按照社会阶层被分成三个空间，城市尺度由空间和时间双重折叠，不同阶层所处的空间和时间都是不平等的，映射出当代社会中人们对于阶层割裂趋势的深切焦虑。

在指数级增长的时代，在高节奏高压力快速扩张的城市生活中，只有像纸团一样，将自己升维，尽可能容纳更多的褶皱，这就像人体的大脑，脑沟和脑回构成的褶皱使脑颅里的大脑皮层面积增加，从而在哺乳脑之上，产生出完全不同的物种。

启示三：生命在于折腾

健康心脏的心电图变化更多，分形维数相对更高；而生病的心脏则有着相对平缓的心电图，分形维数更小。

外界持续的冲击和改变，要求你的器官，即灵活又要有弹性，也因此要有更大的分形维数。

健康和强壮等同于更大的变化和波动，心电图中的分形维数更大，这与系统的韧性有关。太过僵硬和受限意味着系统缺乏足够的灵活性来进行必要的调整，以抵抗不可避免的小冲击。

小结

无论是产品创新的分形第二曲线，还是创新对多样性的要求，亦或是笔者一直推崇的“一切杀不死你的让你更坚强”的反脆弱理念，在分形理论上同样都得到完美的证实。

在DevOps社区北京峰会上，有人说之所以参加技术社区活动，是因为深深的焦虑感。

《北京折叠》就像被揉成一团的A4纸，即科幻又现实，即合乎情理又异常残酷。

如何破除？唯有不停折腾自己，唯有成为终生学习者，唯有不断让自己升维，与IDCF一同成长！

参考材料

• IDCF黑客马拉松 - 第二曲线创新模块
• 《规模：复杂世界的简单法则》
• 芒德勃罗：沿着博物学传统走来 https://www.pep.com.cn/gzsx/rjbgzsx/rjgzsxwd/201008/t20100827_1473661.html
• 知乎：https://www.zhihu.com/question/265983000/answer/301235097
• 百度百科：https://baike.baidu.com/item/%E5%88%86%E5%BD%A2%E7%90%86%E8%AE%BA/1568038?fr=aladdin

1月7日（周四）晚8点，【冬哥有话说】2021年1月第一期，邀请到业界知名实战派研发效能和软件质量双领域专家茹炳晟老师分享《软件研发效能提升随想录》，识别下图二维码回复“研发效能”可获取直播地址~

?IDCF DevOps黑客马拉松2021年赛事安排点击“阅读原文”或输入地址查看：https://j.mp/35bBHI2