九十四、动态规划系列之路径问题-技术圈

「@Author：Runsen」

在动态规划最短路径经常提及，在上几篇介绍过相关的最短路径的问题，介绍过使用Dijkstra算法去求解，但是Dijkstra算法是基于贪心算法，按路径长度递增的次序一步一步并入来求取，算法效率低效。

Dijkstra算法原理是：如果从图中某一顶点（源点）到达另一顶点（终点）的路径可能不止一条，如何找到一条路径使得沿此路径上各边的权值总和（称为路径长度）达到最小。动态规划可以说算法中最优秀的算法，因为在此介绍动态规划系列中的路径问题。

下面是对应的动态规划解决的路径问题总结：

62. 不同路径
63. 不同路径 II
64. 最小路径和
120. 三角形最小路径和

62.不同路径

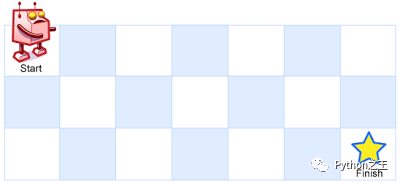
一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

下面是测试用例：

输入：m = 3, n = 7
输出：28

在此，我们可以完全当作一道初中数学题来对待，既然最后要到达终点，那肯定需要往下走n-1步，往右走m-1步，总共需要走n+m-2步。

还有无论往右走还是往下走他的总的步数是不会变的，往右走的步数一定等于n，往下走的步数一定等于m。

因此，可以换一种说法相当于总共要走n+m-2步，往右走m-1步，总共有多少种走法，很明显这就是一个高中数学的排列组合问题，公式如下

排列组合的计算公式：

代入就可以得到：

# factorial求阶乘，也可以自己定义一个
import math 
def uniquePaths(self, m: int, n: int) -> int:
        return int(math.factorial(m+n-2)/math.factorial(m-1)/math.factorial(n-1))

上面的方法没有开数组空间，无论是时间还是空间，都是最优的做法。

对于动态规划的方法，也非常容易理解，定义一个二维数组dp，来存储每一个格子的最短路径数之和，设 dp 为大小矩阵，其中 dp[i][j] 的值代表直到走到 (i,j) 的最小路径和。

由于只能向右向下移动，所以对于除了边界外的格子之外的其他格子而言，到达它的方式只能有它上边的格子下移或者左边的格子右移，所以到达它的路径数为它上边格子的路径数与左边格子的路径数之和，可得状态转移方程：dp[i][j] = dp[i-1][j] + dp[i][j-1]。

下图是二维数组动态规划求解的过程：

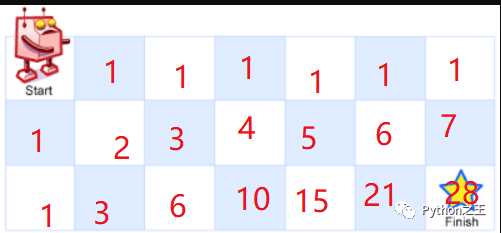
dp初始化，对于第一行 dp[0][j]，或者第一列 dp[i][0]，由于都是在边界，所以只能为 1。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0] * n for _ in range(m)]

        # 初始化
        for i in range(m):
            dp[i][0] = 1
        
        for j in range(n):
            dp[0][j] = 1

        # 根据转移方程进行递推
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
        
        return dp[-1][-1]

当然，你也可以对二维dp数组压缩成一维数组，来代表每一行或者每一列的路径数之和，可以对空间进一步的优化。

63. 不同路径 II

此题和第一题的添加了一个障碍物，那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

测试用例：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

假设自己画的方框是障碍物，那么直接把二维数组对应的位置变成0即可。

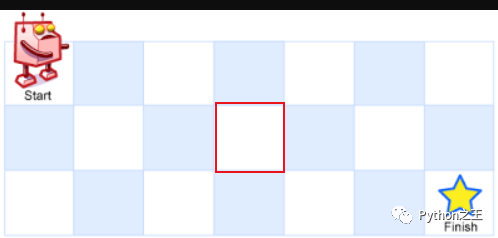
因此，最终的解决过程：

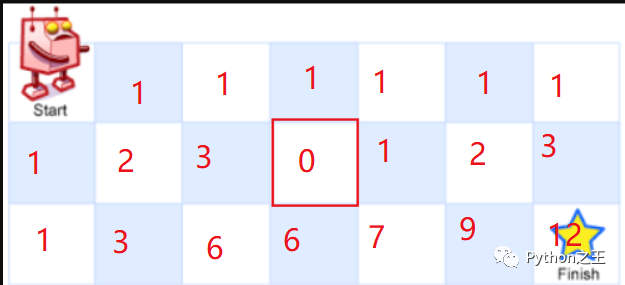
在此题中，测试用例存在门口就是一个障碍物的情况，因此需要注意初始化条件。

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m, n = len(obstacleGrid), len(obstacleGrid[0])
        # 门口是一个障碍物
        if obstacleGrid[0][0] == 1:
            return 0
        dp = [[0 for _ in range(n)] for _ in range(m)]
        dp[0][0] = 1
        
        for i in range(1, m):
            if obstacleGrid[i][0] == 0:
                dp[i][0] = dp[i-1][0]
                
        for j in range(1, n):
            if obstacleGrid[0][j] == 0:
                dp[0][j] = dp[0][j-1]
        
        for i in range(1, m):
            for j in range(1, n):
                # 判断是不是障碍物
                if obstacleGrid[i][j] == 1:
                    dp[i][j] = 0
                else:
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        return dp[-1][-1]

64. 最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

测试用例:

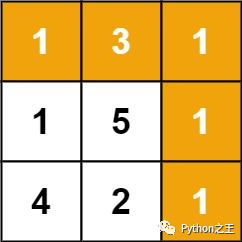
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

如果采用贪心的算法，会由于顾及当前的利益，而放弃长远的利益。因此贪心的思路直接否决。

在此题的动态规划中，状态转移方程仍是：dp[i][j] = dp[i-1][j] + dp[i][j-1]。

初始化dp所有的元素均为0，在网格的第一行和第一列的所有路径和应该都是固定的，因为都是向右或者向下移动。

而当位置(i,j)处时，需要从判断从向右和向下的dp的数值，取出最小值，然后加上这个网格的数字。

dp[i][j] = min(dp[i-1][j] +grid[i][j]，dp[i][j-1]++grid[i][j])

from typing import List
class Solution:
    def minPathSum(self, grid: [[int]]) -> int:
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if i == j == 0: continue
                elif i == 0:  
                    grid[i][j] = grid[i][j - 1] + grid[i][j]
                elif j == 0:  
                    grid[i][j] = grid[i - 1][j] + grid[i][j]
                else: grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j]
        return grid[-1][-1]


if __name__ == "__main__":
    s=Solution()
    t=[[1,3,1],
      [1,5,1],
      [4,2,1]]
    print(s.minPathSum(t))
# result
7

120. 三角形最小路径和

此题三角形最小路径和变换了输入的矩阵，给定一个三角形 triangle ，找出自顶向下的最小路径和。

测试用例

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3

2
3 4
6 5 7    
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

此题由于空间在压缩，因此使用一维动态归化数组，定义dp[i]为到第N层第i个节。

要想获得到达第 m 条边的最小路径和，需要先获得到达第m - 1 条边的最小路径和。

由于动态规划可以采用自底向上的逆推思想，也就是把三角形倒过来看。

状态转移方程：dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j]

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        dp = triangle[-1]
        for i in range(len(triangle)-2,-1,-1):
            for j in range(i+1):
                dp[j] = triangle[i][j] + min(dp[j],dp[j+1])
        return dp[0]

对于原地自顶向下算法，把到达每一层的每个数的最小路径都算出来，判断三种不同状态的，根据下面的状态转移方程，不断地修改原数组。

自顶向下算法可以直接用triangle本身的变量进行计算，达到减小内存开销的效果。

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        if len(triangle)==0: 
            return 0
        #动态规划 dp表示走到当前位置的时候的最小路径
        for i in range(1,len(triangle)):
            for j in range(len(triangle[i])):
                if j==0: #最左边的情况
                    triangle[i][j]+=triangle[i-1][j]
                elif j==i: #最右边的情况
                    triangle[i][j]+=triangle[i-1][j-1]
                else:
                    triangle[i][j]+=min(triangle[i-1][j-1],triangle[i-1][j])
        return min(triangle[-1]) #返回最后一层最小的一个

更多的文章

点击下面小程序

- END -