规划问题之线性规划【笔记】
例题
以下面线性规划为例,求的最小值
方法一:使用scipy库
预备知识
scipy.optimize.linprog
语法
scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='interior-point', callback=None, options=None, x0=None)
常用参数:
c:所求目标函数未知数的系数集合
A_ub:不等式左边未知数的系数集合
B_up,不等式右边数值集合
A_eq,等式左边未知数的系数集合
B_eq ,等式右边的数值集合
bounds:每个未知数的限制集合 ,默认每个未知数限制条件为(0,None)
method:用于解决标准形式问题的算法。默认为interior-point
常用返回值:
fun:float,目标函数的最优值。(求解目标函数的 最小值 )
x:一维数组,在满足约束条件的同时使目标函数最小化的决策变量的值。
status:int,表示算法退出状态的整数。
0:优化成功终止。 1:迭代极限达到。 2:这个问题似乎不可行。 3:问题似乎是无界的。 4:遇到数值困难。 nit:int,在所有阶段中执行的迭代的总数。
message:str,表示算法退出状态的字符串描述符。
API官方解释:
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html
解答
首先,将约束修改为标准模式:不等式只能含有 小于等于
编写代码
from scipy import optimize
import numpy as np
# 目标函数未知数的系数
c = np.array([2,3,-5])
# 不等式左边未知数的系数集合(二维数组,因为不止一个不等式)
# 第一个不等式的系数是【-2,5,-1】
# 第二个不等式的系数是【1,3,1】
A_ub = np.array([[-2,5,-1],[1,3,1]])
# 不等式右边数值的集合(一维数组)
# 第一个不等式右边数值是-10
# 第二个不等式右边数值是12
b_ub = np.array([-10,12])
# 等式左边的系数集合(二维数组)
A_eq = np.array([[1,1,1]])
# 等式右边的数值(一维)
b_eq = np.array([7])
# 使用optimize.linprog进行求解
res = optimize.linprog(c,A_ub,b_ub,A_eq,b_eq)
res
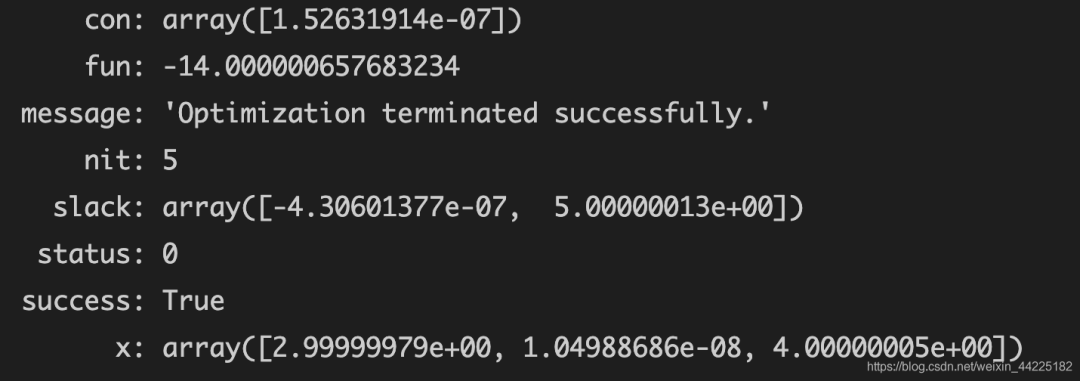
运行结果
最优解(最小值):-14.000000657683234 最优解对应的: array([2.99999979e+00, 1.04988686e-08, 4.00000005e+00])
补充 - 1
倘若需要求 的最大值 ?
scipy.optimize.linprog 只能求目标函数最小值
若需要求目标函数最大值 ,只需要将函数中参数改为 -c
❝因为在求一个函数的最大值时,我们可以求取反(乘以-1)后目标函数的最小值
对最小值再乘以-1 即可得到最大值
比如函数 x1 + x2 的最大值是2(事先不知道)
我们可以先求 -(x1 + x2) 的最小值
通过求解找出-(x1 + x2) 的最小值为 -2
那么最大值就是 -2 * -1 = 2
Demo代码
from scipy import optimize
import numpy as np
c = np.array([2,3,-5])
A_ub = np.array([[-2,5,-1],[1,3,1]])
b_ub = np.array([-10,12])
A_eq = np.array([[1,1,1]])
b_eq = np.array([7])
res = optimize.linprog(-c,A_ub,b_ub,A_eq,b_eq)
res
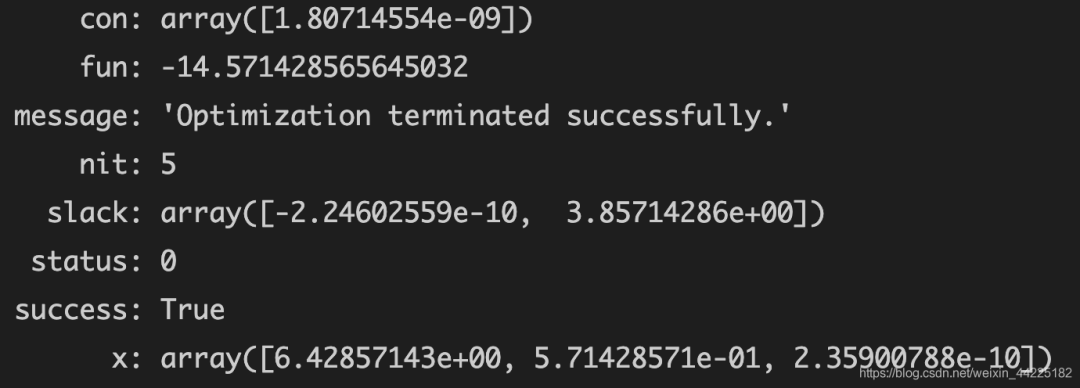
运行结果:
最优解,最大值是:14.571428565645032(我们求的是-c的最小值,为-14.571428565645032,那么c的最大值就是 14.571428565645032) 对应最优解: array([6.42857143e+00, 5.71428571e-01, 2.35900788e-10])
补充 - 2
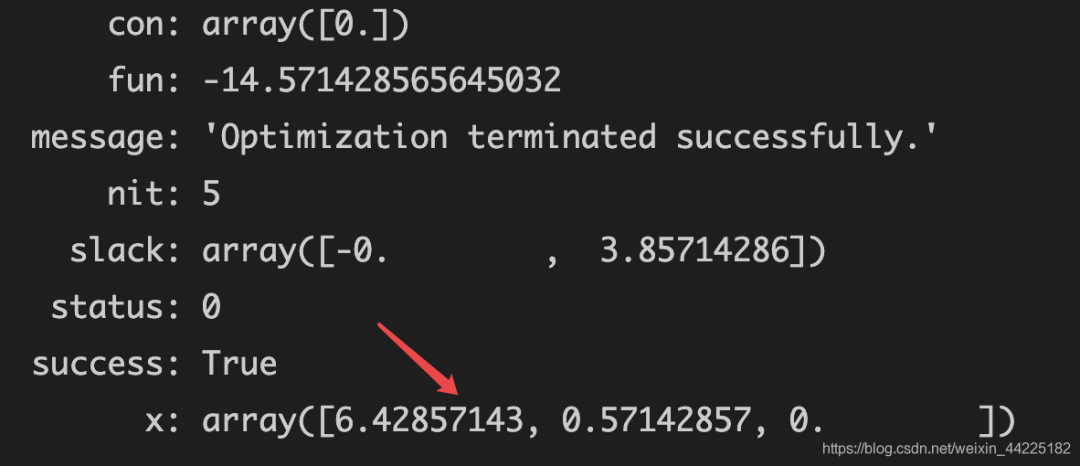
可以发现最后结果中数据是以科学记数法表示的
倘若不需要科学技术法进行表示
添加代码np.set_printoptions(suppress=True) 即可
Demo代码
from scipy import optimize
import numpy as np
np.set_printoptions(suppress=True)
c = np.array([2,3,-5])
A_ub = np.array([[-2,5,-1],[1,3,1]])
b_ub = np.array([-10,12])
A_eq = np.array([[1,1,1]])
b_eq = np.array([7])
res = optimize.linprog(-c,A_ub,b_ub,A_eq,b_eq)
res
运行结果
补充 - 3
在前面的例子中,的范围为 x >= 0 , 属于scipy.optimize.linprog中参数 bounds 的默认值(0, None)
None:表示无限制
那么如果 有范围限制该如何求解呢?
