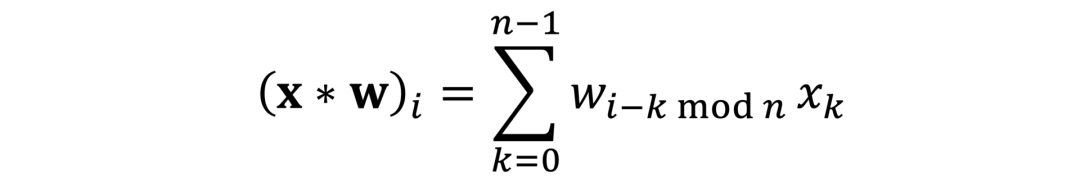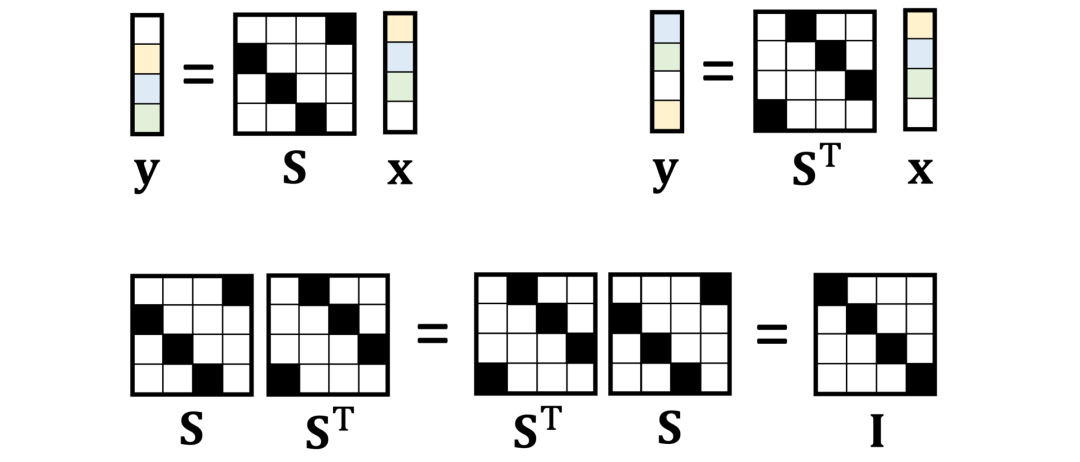点击上方“程序员大白”,选择“星标”公众号
重磅干货,第一时间送达

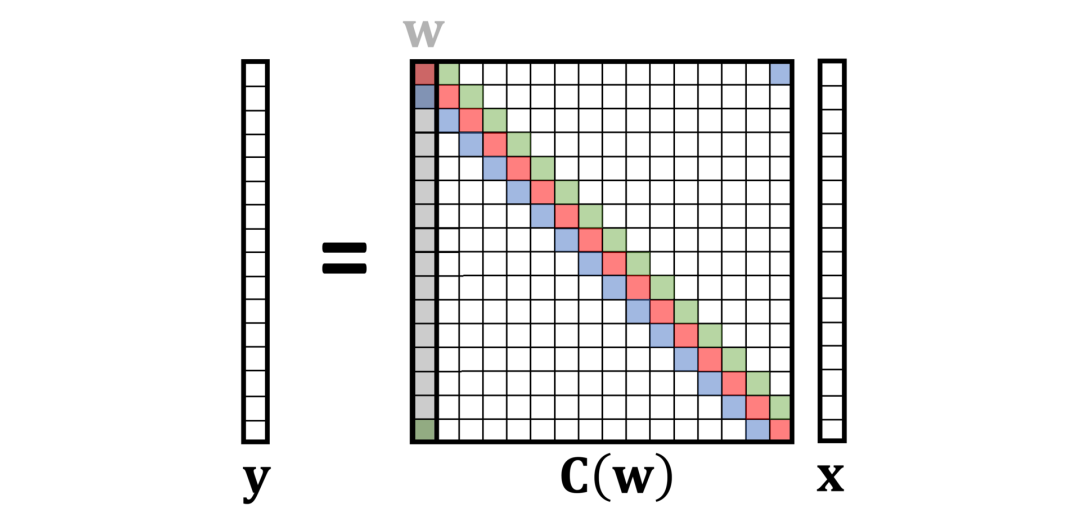
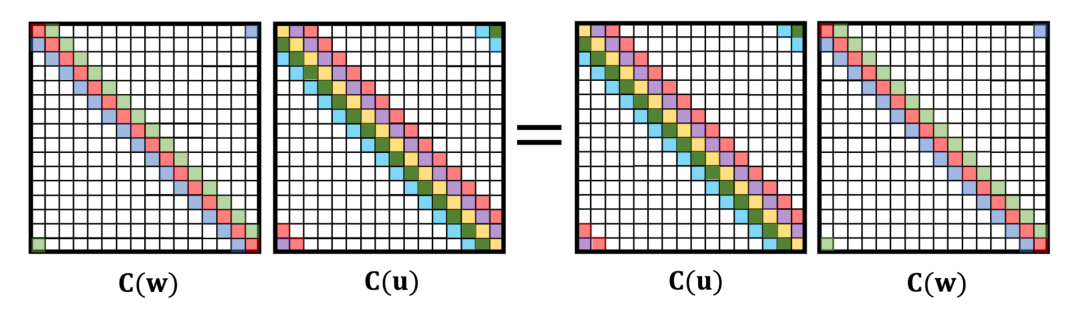
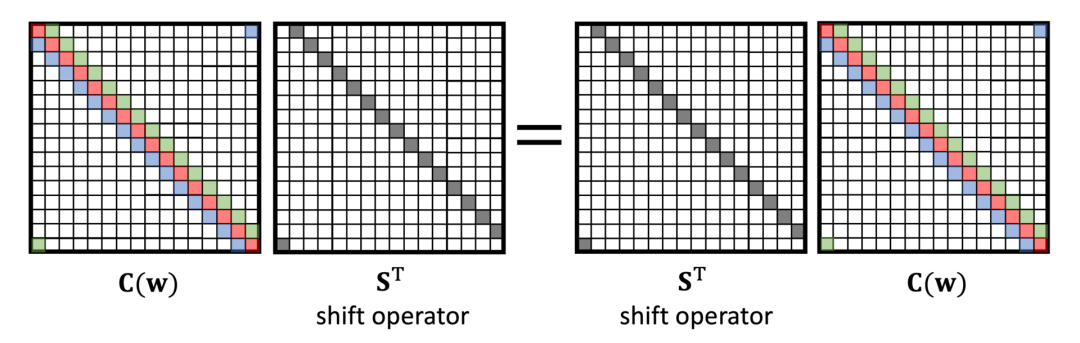
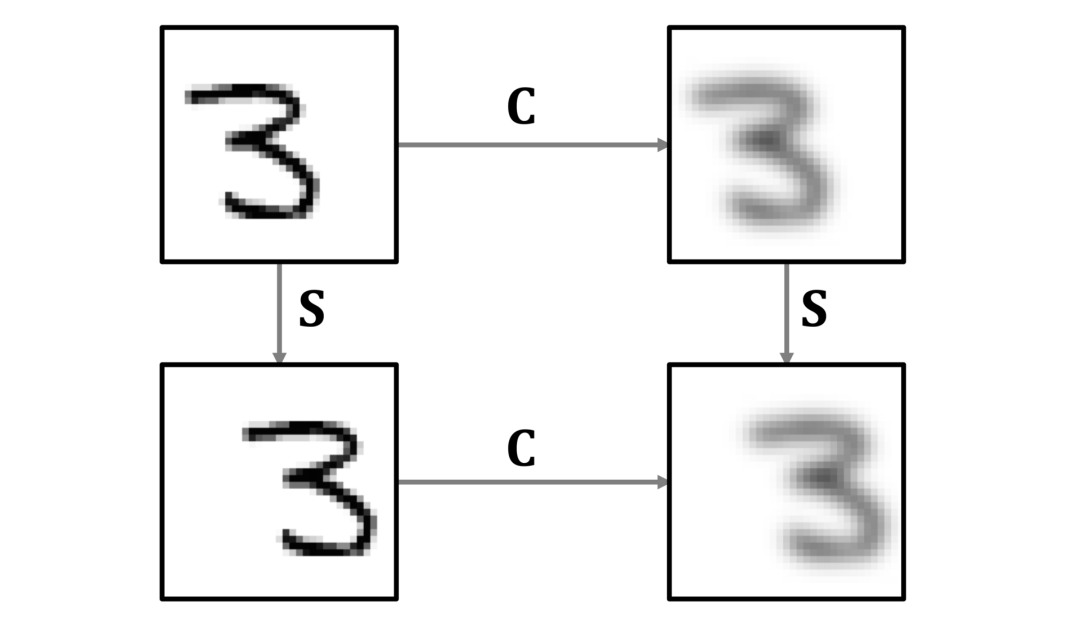
卷积的概念无处不在。它究竟有什么特别之处呢?在本文中,作者从第一性原理中推导出卷积,并表明它自然地来自平移对称性。在阅读卷积的起源与历史的过程中,读者有机会了解到卷积概念和卷积运算符的发展历史。卷积积分最早是出现在法国著名数学家达朗贝尔在1754年发表的著作《宇宙体系的几个要点研究》(Recherches sur différents points importants du système du monde)里所介绍的泰勒定理推导中。人们常误以为卷积积分最早是出现在法国数学家拉普拉斯1773年的论文《行星轨道的平均倾角、地球形状与函数》(Mémoire sur l’inclinaison moyenne des orbites des comètes, sur la figure de la terre et sur les fonctions中,但实际上,拉普拉斯是在1778年撰写概率论时才真正使用卷积。在早期,卷积被尝试命名为法语“résultante”、意大利语“composizione”、德语“faltung”等,均指向“折叠”、“卷曲”之类的含义。英语用来指代“卷积”的单词“convolution”取自拉丁文“con”(together,“一起”)和volvere(roll up,“卷起”),使德语“faltung”的直译,最早出现在Aurel Friedrich Wintner发表于1934年的论文中,后来又被Gustav Doetsch(现代拉普拉斯变换理论的奠基人)等知名数学家在权威作品中引用,所以“convolution”的地位也由此得以巩固。沃尔泰拉(Volterra)最早在1910年使用星星运算符(*),但形状稍有不同。卷积的现代表现形式“f∗g”最早是由Gustav Doetsch在1923年提出的。日前,帝国理工教授Michael Bronstein在《Deriving convolution from first principles》中从第一性原理即平移不变性或对称性(translational invariance or symmetry)推导出卷积,而不是事先假设卷积的存在。这个脑洞看似平平无奇,但效果却惊掉下巴!基础的信号处理课程中教过一个公式,这个公式对含有两个n维向量x和w的离散卷积(discrete convolution,此处特指“循环卷积”)作了如下定义:在这里,为了方便理解与阅读,作者假设所有索引的取值范围为0到n-1,并对n取模。将上面的公式写成矩阵向量乘法,会得到一个循环矩阵,如下图所示:循环矩阵具有多对角线结构(multi-diagonal structure),每个对角线上的元素有相同的值。它可以通过堆叠向量w的平移向量(对n取模)来形成。因此,这里使用符号C(w)来指代由向量w形成的循环矩阵。因为所有卷积x∗w都可以等同于循环矩阵C(w)x的乘积,所以x∗w和C(w)x这两项表达在本文中会交替使用。 我们知道在线性代数中,矩阵乘法是非交换的,比如说,一般情况下AB≠BA。但是,循环矩阵是一个非常特殊的例外:循环矩阵可交换。换句话说,C(w)C(u)=C(u)C(w)。这条法则适用于所有循环矩阵或向量u和w。同样地,我们可以说,卷积运算是遵循交换律的,即x∗w=w∗x。若w=[0,1,0…,0],则C(w)是一个能将向量往右移动一个位置的特殊循环矩阵。该矩阵称为(右)平移运算符(作者将“运算符”与“矩阵”交换使用),用S表示。右平移运算符的转置为左移位运算符。很显然,向左移动,然后向右移动并没有任何作用,反之亦然。这表明,S是正交矩阵(orthogonal matrix):循环矩阵的特点在于可交换性。Bamieh2018年的论文《Discovering transforms: a tutorial on circulant matrices, circular convolution, and the discrete Fourier transform》中的引理3.1指出:当且仅当矩阵是平移可交换的时候,这个矩阵才能称为“循环矩阵”。首先,这表明循环矩阵具有一个非常重要的属性,即平移等变性(translation equivariance):卷积的平移可交换性表明,先平移向量然后进行卷积,或先卷积再平移,结果是一样的。注意:有些同学容易混淆“invariance”与“equivariance”的概念,前者指的是“unchanged”,不变,后者指的是“changing in the same way”,通过同样的方式进行改变。许多信号处理的教科书也会将作者此处谈到的“shift equivariance”(平移等变性)说成“shift invariance”(平移不变性)。如果f(Sx)=Sf(x),则函数为平移等变性;如果f(Sx)=f(x),则函数为平移不变性。“平移不变性”是物理学中的一个基础概念,经常以“平移对称性”的说法出现,指的是物理法则独立于空间内的地理位置。在经典力学的变分公式中,根据诺特定理(Noether's theorem),动量守恒的基本法则是由平移不变性导出。其次,卷积可以定义为“平移-等变线性运算”:为了满足平移可交换,矩阵必须具有循环结构。这正是我们一开始所希望的,就是将卷积从平移对称性的第一性原理中推导出来。作者没有不加辨别地接受信号处理课程教材书给出的卷积公式、证明它的平移等变性(shift equivariance)性质,而是从平移等变性出发,再得出卷积公式是唯一满足的线性操作。图注:平移等变性的展示,即平移和模糊操作是可交换的。卷积和傅里叶变换
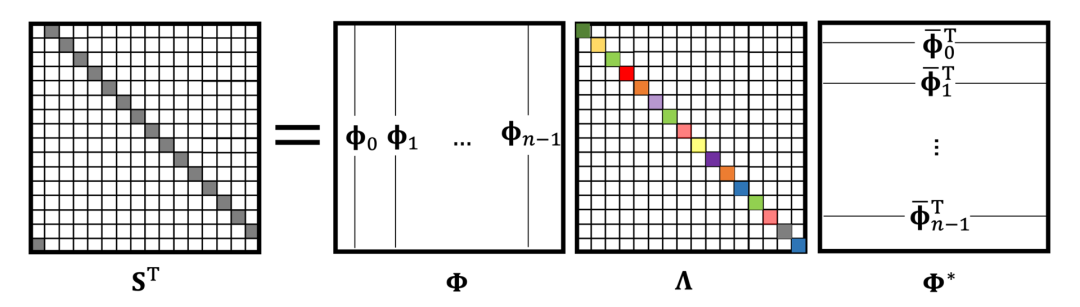
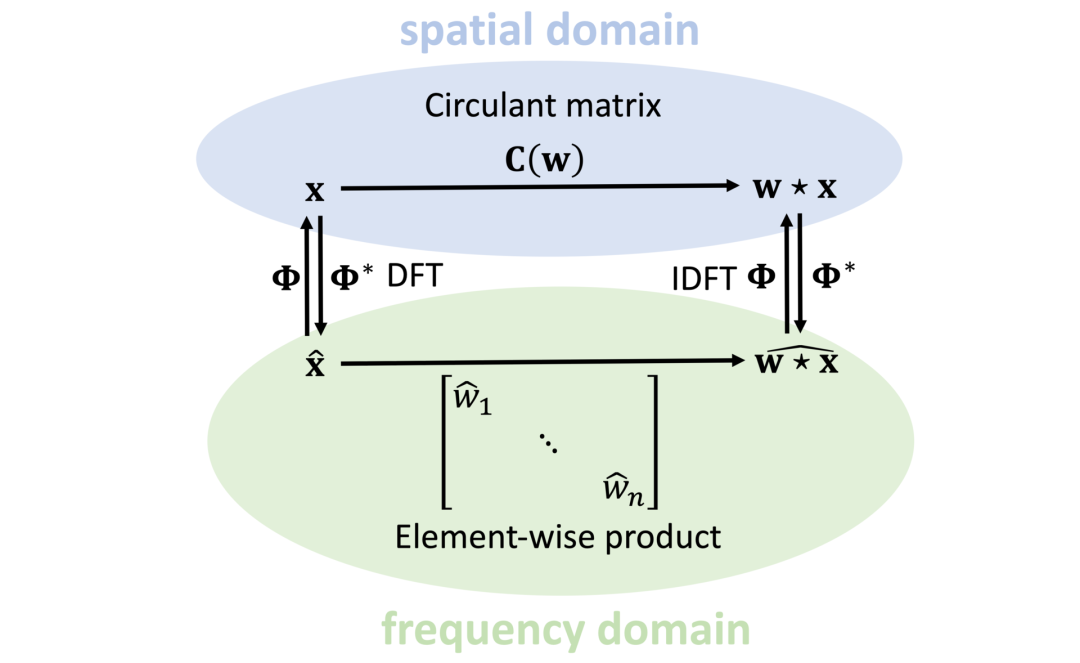
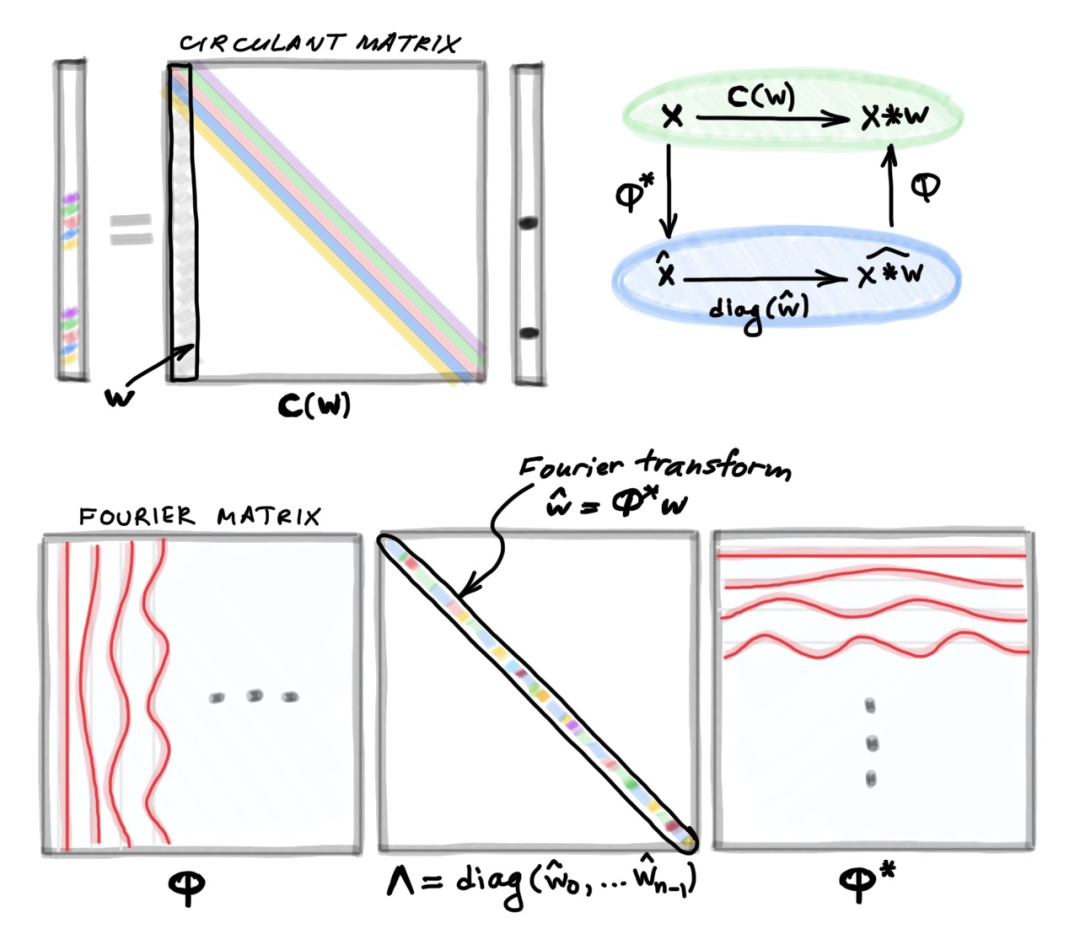
信号处理课程中还讲到另一个重要现象,即卷积和傅里叶变换(Fourier transform)之间的联系。由于我们此处探讨的是有限维向量(finite-dimensional vectors),所以此处“傅里叶变换”指的是“离散傅里叶变换”(Discrete Fourier Transform,DFT)。傅里叶变换能将卷积运算对角化,从而将在频域内执行两个向量的卷积作为它们傅里叶变换的逐元素乘积。没有人能解释傅里叶变换中正弦和余弦的来源以及它们的特殊之处。为了进行更深入的研究,我们要回顾线性代数中的一个事实:交换矩阵可以联合对角化。换句话说,满足AB=BA的两个矩阵将具备相同的特征向量(但可能特征值不同)。更确切地说,联合对角化意味着两个交换矩阵具有相同的本征空间,因为在一般情况下,本征值具有非平凡的多重性(non-trivial multiplicity)。由于在这里作者讨论的所有特征值都很简单,因此只围绕一个共同的特征基进行讨论。由于所有循环矩阵都是可交换的,因此我们可以选择其中一个矩阵,并计算它的特征向量(上述定理确保了这些向量也是所有循环矩阵的特征向量)。为方便起见,我们选择平移运算符S。由于S是正交矩阵,所以我们也期望其特征向量是正交的。论文《DISCOVERING TRANSFORMS: A TUTORIAL ON CIRCULANT MATRICES, CIRCULAR CONVOLUTION, AND THE DISCRETE FOURIER TRANSFORM》中的4.1节中通过简单的计算得出以下结论:“傅里叶变换能将平移运算符对角化”。但是,由于S是非对称的,因此它没有实数特征值(对称的实数矩阵具有实数特征值)。S的特征值恰好是单位矩阵的复数根。接下来是这篇文章的第二个“震惊”发现:这正是正弦与余弦的来源!它们是平移运算符的特征向量,作者将它们称为矩阵的列Φ。需要注意的是,特征向量是复数,因此在转置Φ时需要进行复数共轭。与Φ*相乘(从左边开始)被称为“傅里叶变换”,而与Φ相乘被称为“傅里叶逆变换”。由于所有循环矩阵都可以联合对角化,因此它们也可以通过傅里叶变换进行对角化。循环矩阵仅在特征向量上有所区别。最后一个常被忽视的点是:C(w)的特征值是向量w的傅里叶变换。此处矩阵C通过傅里叶变换“对角化”,指的是矩阵Φ*CΦ是对角的。由于傅里叶变换是一个正交矩阵(Φ*Φ= I),因此在几何上,它起着相当于n维旋转的坐标系变化的作用。在此坐标系中,C的作用变为按元素的乘积。上述的结论可以总结为一个卷积定理:卷积x∗w可以看作在原始坐标系上将循环矩阵C(w)作用于x(有时称为 “空间域”卷积);或者在傅里叶的基础上(“频谱域”),先计算Φ*x的傅里叶变换,再乘以w的傅里叶变换,然后计算傅里叶逆变换。因为Φ具有特殊的冗余结构,所以可以用快速傅里叶变换(FFT)算法以𝒪(n log n)复杂度将Φ*x和Φx的结果计算出来。为什么卷积的这个定义如此重要、并需要通过这种方式进行讲解呢?作者引用了爱尔维修(Helvétius)的一句话:“The knowledge of certain principles easily compensates the lack of knowledge of certain facts.”(“有些原理所包含的知识能轻巧弥补某些事实的知识空缺”。)在卷积的案例中,它的第一性原理(平移对称性)推导过程能很轻松地推广到其他领域。1、https://towardsdatascience.com/deriving-convolution-from-first-principles-4ff124888028
2、https://arxiv.org/pdf/1805.05533