【统计学习方法】 第5章 决策树(一)

决策树是一种基本的分类与回归方法。本篇主要讨论用于分类问题的决策树。决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。其主要优点是模型具有可读性,分类速度快。学习时,利用训练数据,根据损失函数最小化的原则建立决策树模型。预测时,对新的数据,利用决策树模型进行分类。
决策树学习通常包括3个步骤:特征选择,决策树的生成和决策树的修剪。
1
●
决策树模型
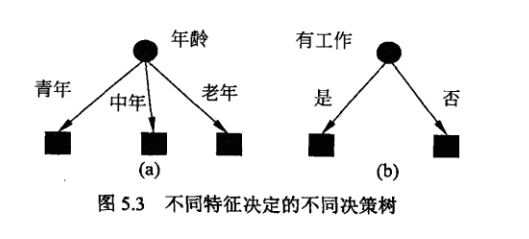
决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。用决策树分类,从根节点开始,对实例的某一特征进行测试,根据测试结果,将实例分配到其子节点;这时,每一个子节点对应着该特征的一个取值。如此递归。
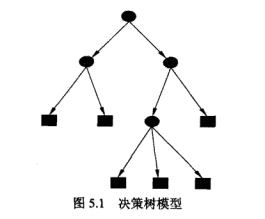
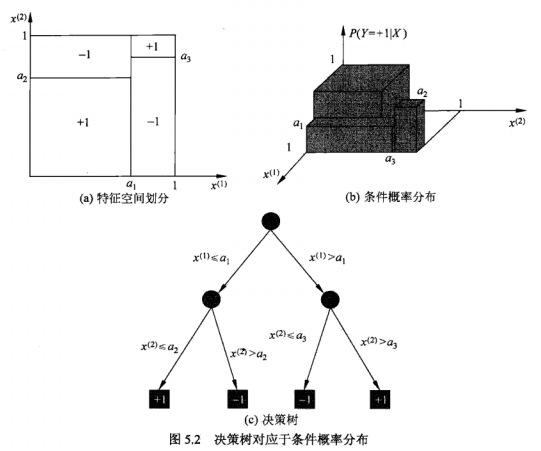
决策树还表示给定特征条件下类的条件概率分布。这一条件概率分布定义在特征空间的一个划分上。
决策树学习
决策树学习,假设给定训练数据集
其中,
决策树学习本质上是从训练数据集中归纳一组分类规则。与训练数据集不相矛盾的决策树可能有多个,也可能一个都没有。我们需要的是一个与训练数据矛盾较少的决策树,同时具有很好的泛化能力。
2
●
特征选择
特征选择问题
特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树的学习效率。通常特征选择的准则是信息增益或信息增益比。
信息增益:
在信息论与概率统计中,熵是表示随机变量不确定性的度量。设X是一个取有限个值的离散随机变量,其概率分布为:
则随机变量X的熵定义为
由定义可知,熵只依赖于X的分布,而与X的取值无关,所以也可以将X的熵记作
熵越大,随机变量的不确定性就越大。
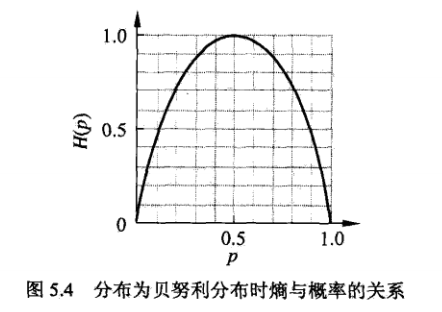
设有随机变量
条件熵
当熵和条件熵中的概率由数据估计得到时,所对应的熵与条件熵分别称为经验熵和经验条件熵。
信息增益表示得知特征X的信息而使得类Y的信息不确定性减少的程度。
特征A对训练数据集D的信息增益
决策树学习应用信息增益准则选择特征。给定训练数据集D和特征A,经验熵
3
●
例题5.1
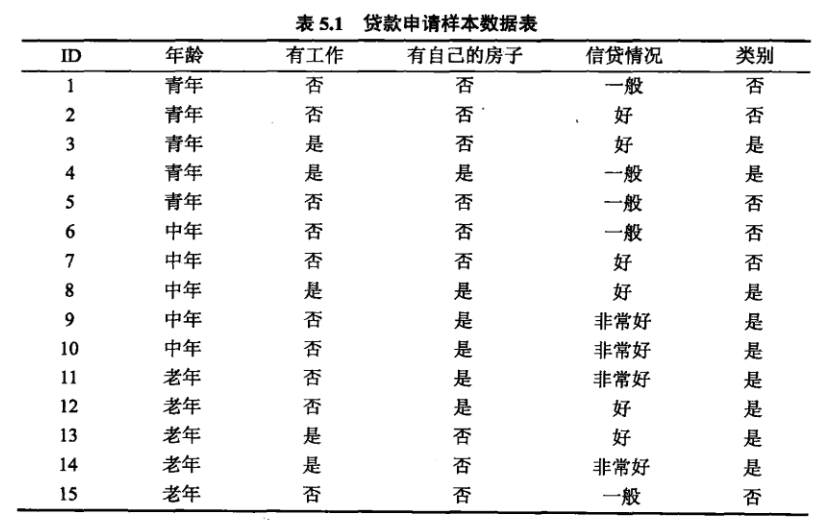
问题:
希望通过所给的训练数据学习一个贷款申请的决策树,用以对未来的贷款申请进行分类,即当新的客户提出贷款申请时,根据申请人的特征利用决策树决定是否批准贷款申请。
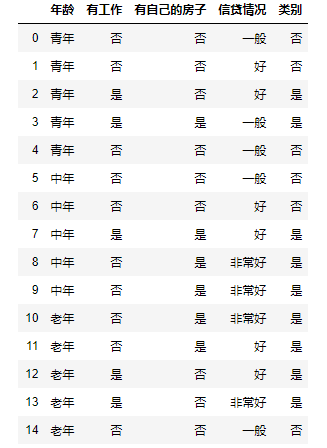
创建数据集
def create_data():datasets = [['青年', '否', '否', '一般', '否'],['青年', '否', '否', '好', '否'],['青年', '是', '否', '好', '是'],['青年', '是', '是', '一般', '是'],['青年', '否', '否', '一般', '否'],['中年', '否', '否', '一般', '否'],['中年', '否', '否', '好', '否'],['中年', '是', '是', '好', '是'],['中年', '否', '是', '非常好', '是'],['中年', '否', '是', '非常好', '是'],['老年', '否', '是', '非常好', '是'],['老年', '否', '是', '好', '是'],['老年', '是', '否', '好', '是'],['老年', '是', '否', '非常好', '是'],['老年', '否', '否', '一般', '否'],]labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']# 返回数据集和每个维度的名称return datasets, labelsdatasets, labels = create_data()train_data = pd.DataFrame(datasets, columns=labels)
计算熵:
def calc_ent(datasets):data_length = len(datasets)label_count = {}for i in range(data_length):label = datasets[i][-1]if label not in label_count:label_count[label] = 0label_count[label] += 1ent = -sum([(p / data_length) * log(p / data_length, 2)for p in label_count.values()])return ent
条件经验熵:
def cond_ent(datasets, axis=0):data_length = len(datasets)feature_sets = {}for i in range(data_length):feature = datasets[i][axis]if feature not in feature_sets:feature_sets[feature] = []feature_sets[feature].append(datasets[i])cond_ent = sum([(len(p) / data_length) * calc_ent(p) for p in feature_sets.values()])return cond_ent
信息增益:
def info_gain(ent, cond_ent):return ent - cond_ent
def info_gain_train(datasets):count = len(datasets[0]) - 1ent = calc_ent(datasets)# ent = entropy(datasets)best_feature = []for c in range(count):c_info_gain = info_gain(ent, cond_ent(datasets, axis=c))best_feature.append((c, c_info_gain))print('特征({}) - info_gain - {:.3f}'.format(labels[c], c_info_gain))# 比较大小best_ = max(best_feature, key=lambda x: x[-1])return '特征({})的信息增益最大,选择为根节点特征'.format(labels[best_[0]])
info_gain_train(np.array(datasets))
END
